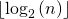Preguntas de práctica para la recursividad | conjunto 2

Explique la funcionalidad de las siguientes funciones. 

Pregunta 1 

/* Assume that n is greater than or equal to 1 */
int fun1(int n)
{
    if (n == 1)
        return 0;
    else
        return 1 + fun1(n / 2);
}

/* Assume that n is greater than or equal to 1 */
static int fun1(int n)
{
    if (n == 1)
        return 0;
    else
        return 1 + fun1(n / 2);
}

# Assume that n is greater than or equal to 1 */
def fun1(n):
    if(n == 1):
        return 0
    else:
        return 1 + fun1(n//2)

/* Assume that n is greater than or equal to 1 */
static int fun1(int n)
{
    if (n == 1)
        return 0;
    else
        return 1 + fun1(n / 2);
}

<script>
 
/* Assume that n is greater than or equal to 1 */
function fun1(n)
{
    if (n == 1)
        return 0
    else
        return 1 + fun1(Math.floor(n / 2))
}
</script>

Respuesta: La función calcula y devuelve

Por ejemplo, si n está entre 8 y 15, fun1() devuelve 3. Si n está entre 16 y 31, fun1() devuelve 4.

Pregunta 2 

/* Assume that n is greater than or equal to 0 */
void fun2(int n)
{
if(n == 0)
    return;
 
fun2(n/2);
cout << n%2 << endl;
}

/* Assume that n is greater than or equal to 0 */
void fun2(int n)
{
  if(n == 0)
    return;
 
  fun2(n/2);
  printf("%d", n%2);
} 

/* Assume that n is greater than or equal to 1 */
static void fun2(int n)
{
if(n == 0)
    return;
  
fun2(n/2);
System.out.println(n%2);
}

# Assume that n is greater than or equal to 0 */
def fun2(n):
    if(n == 0):
        return
     
    fun2(n // 2)
    print(n % 2, end="")

void fun2(int n)
{
if(n == 0)
    return;
   
fun2(n/2);
Console.Write(n%2);
}

<script>
 
// Assume that n is greater than or equal to 1
function fun2(n)
{
    if (n == 0)
        return;
     
    fun2(Math.floor(n / 2));
    document.write(n % 2 + " ")
}
</script>

Respuesta: La función fun2() imprime el equivalente binario de n. Por ejemplo, si n es 21, fun2() imprime 10101. 

Nota: Las funciones anteriores son solo para practicar la recursividad, no son la implementación ideal de la funcionalidad que brindan. 

Escriba comentarios si encuentra alguna de las respuestas/códigos incorrectos.