Principio de Inducción Matemática

La inducción matemática es un método de prueba matemática que se utiliza para probar una declaración dada sobre cualquier conjunto bien organizado. Generalmente, se utiliza para probar resultados o establecer enunciados que se formulan en términos de n, donde n es un número natural. La técnica involucra tres pasos para probar un enunciado, P(n), como se indica a continuación:

Verifique si la afirmación es verdadera para casos triviales como n = a, es decir, P(a) es verdadera. [Caso base]
Suponga que el enunciado es verdadero para n = k para algún k ≥ a, es decir, P(k) es verdadero. [Hipótesis inductiva]
Si la verdad de P(k) implica la verdad de P(k + 1), entonces el enunciado P(n) es verdadero para todo n ≥ a .

El paso base y el paso inductivo, juntos, prueban que P(k) => P(k + 1) => P(k + 2) …. es verdad. Por lo tanto, P(n) es cierto para todos los enteros n ≥ a. Podemos comparar la inducción matemática con fichas de dominó que caen. Cuando cae un dominó, derriba el siguiente dominó en sucesión. La primera ficha de dominó derriba a la segunda, la segunda derriba a la tercera y así sucesivamente. Al final, todas las fichas de dominó se tirarán. Pero hay algunas condiciones que deben cumplirse:

El dominó inicial debe caer para poner en marcha el proceso de golpear. Este es el paso básico.
La distancia entre las fichas de dominó debe ser igual para dos fichas de dominó adyacentes. De lo contrario, una determinada ficha de dominó puede caer sin que la siguiente se desplace. Entonces la secuencia de reacciones se detendrá. Mantener la misma distancia entre fichas de dominó asegura que P(k) ⇒ P(k + 1) para cada entero k ≥ a. Este es el paso inductivo.

Ejemplos

Ejemplo 1: Para todo n ≥ 1, prueba que,
1 ² + 2 ² + 3 ² ….n ² = {n(n + 1) (2n + 1)} / 6

Solución:

Sea el enunciado dado P(n),

$P(n)=1^2+ 2^2 + 3^2+ ……+ n^2 = \frac{n(n + 1) (2n + 1)}{6} \ for\, n=1,\ P(1)=\frac{1(1+1)(2*1+1)}{6} = 1\ ,which\ is\ true.$

Ahora, tomemos un número entero positivo, k, y supongamos que P(k) es cierto, es decir,

$1^2 + 2^2 + 3^2 ....k^2 = \frac{k(k+1)(2k+1)}{6}$

Ahora probaremos que P(k + 1) también es cierto, así que ahora tenemos,

PAG(k + 1) = PAG(k) + (k + 1) ²

$= \frac{k(k+1)(2k+1)}{6} + (k+1)^2 \\ \ \\ = \frac {k(k+1)(2k+1)+6{(k+1)}^2}{6} \\ \ \\ = (k+1) \frac{( 2k^2 + k) + 6(k+1)}{6} \\ \ \\ =\frac{(k+1)(2k^2 +7k+6)}{6} \\ \ \\ =\frac{(k+1) (k+2) (2k+3)}{6}\\ \ \\ =\frac{(k+1) ((k+1)+1) (2(k+1) +1)}{6} \ \\$

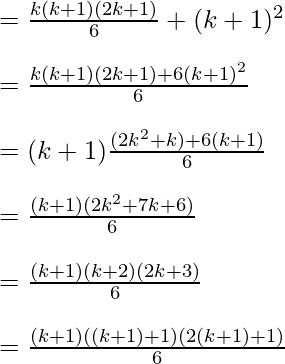
Por tanto, P(k + 1) es verdadero, siempre que P(k) sea verdadero para todos los números naturales. Por lo tanto, por el proceso de inducción matemática, el resultado dado es verdadero para todos los números naturales.

Ejemplo 2: Para todo n ≥ 1, probar que,
1.2.3 + 2.3.4 + 3.4.5 …n(n + 1) (n + 2) = {n (n + 1) (n + 2) ( n + 3)} / 4

Solución:

Sea el enunciado dado S(n),

$and \ S(n)=1.2.3+ 2.3.4 + 3.4.5+ ……+ n.(n+1)(n+2) = \frac{n(n + 1)(n + 2)(n+3)}{4}\\ \ \\ for\ n=1, \ S(1) = \frac{1(1+1)(1+2)(1+3)}{4} = 6\ ,which\ is\ true. \ \\$

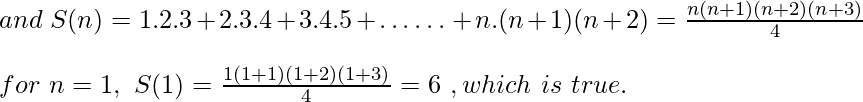
Ahora, tomemos un número entero positivo, k, y supongamos que S(k) es cierto, es decir,

$S(k)=1.2.3+ 2.3.4 + 3.4.5+ ……+ k.(k+1)(k+2) = \frac{k(k+ 1)(k + 2)(k+3)}{4} \ \\$

Ahora probaremos que S(k + 1) también es cierto, así que ahora tenemos,

$S(k+1) = S(k) + (k+1)(k+2)(k+3)\\ \ \\ = \frac{k(k+ 1)(k + 2)(k+3)}{4} + (k+1)(k+2)(k+3)\\ \ \\ = \frac{k(k+ 1)(k + 2)(k+3)+ \ 4(k+1)(k+2)(k+3)}{4} \\ \ \\ = \frac{(k+1)(k+2)(k+3)(k+4)}{4}\\ \ \\ = \frac{ (k+1)\{(k+1)+1\}\{(k+1)+2\}\{(k+1)+3\} }{4}$

Por tanto, S(k + 1) es verdadero, siempre que S(k) sea verdadero para todos los números naturales. E inicialmente mostramos que S(1) es cierto, por lo tanto S(n) es cierto para todos los números naturales.

Ejemplo 3: Para todo n ≥ 1, probar que,
1 + 3 + 5 … 2n – 1 = n ²

Solución:

Sea el enunciado dado S(n),

y S(n) = 1 + 3 + 5 … 2n – 1 = n ²

Para n = 1, 2 * 1 – 1 = 1 ² Por lo tanto, S(1) es verdadera.

Ahora, tomemos un número entero positivo, k, y supongamos que S(k) es cierto, es decir,

S(k) = 1+ 3 + 5 .. (2k – 1) = k ²

Ahora probaremos que S(k + 1) también es cierto, así que ahora tenemos,

1 + 3 + 5 .. (2(k + 1) – 1) = (k + 1) ²

LHS: 1 + 3 + 5 + …. (2k – 1 ) + 2k + 2 – 1

= S(k) + 2k + 1

= k2 ⁺ 2k + 1

= (k + 1) ²

= lado derecho

Por tanto, S(k + 1) es verdadero, siempre que S(k) sea verdadero para todos los números naturales. E inicialmente mostramos que S(1) es cierto, por lo tanto S(n) es cierto para todos los números naturales.

Ejemplo 4: Para todo n ≥ 1, prueba que,
1.2 + 2.3 + 3.4 …n(n + 1) = {n(n + 1)(n + 2)} / 3

Solución:

Sea el enunciado dado S(n),

$and \ S(n)=1.2+ 2.3 + 3.4+ ……+ n.(n+1) = \frac{n(n + 1)(n + 2)}{3}\\ \ \\ for\ n=1, \ S(1) = \frac{1(1+1)(1+2)}{3} = 2\ ,which\ is\ true. \ \\$

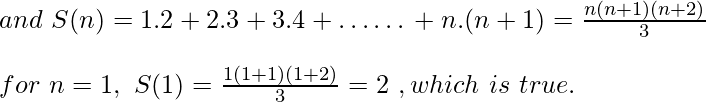
Ahora, tomemos un número entero positivo, k, y supongamos que S(k) es cierto, es decir,

$S(k)=1.2+ 2.3 + 3.4+ ……+ k.(k+1) = \frac{k(k+ 1)(k + 2)}{3} \ \\$

Ahora probaremos que S(k + 1) también es cierto, así que ahora tenemos,

$S(k+1) = S(k) + (k+1)(k+2)\\ \ \\ = \frac{k(k+ 1)(k + 2)}{3} + (k+1)(k+2)\\ \ \\ = \frac{k(k+ 1)(k + 2)+ 3(k+1)(k+2)}{3} \\ \ \\ = \frac{(k+1)(k+2)(k+3)}{3}\\ \ \\ = \frac{ (k+1)\{(k+1)+1\}\{(k+1)+2\} }{3}$

Ejemplo 5: Demuestre que a _n = a ₁ + (n – 1) d, es el término general de cualquier sucesión aritmética.

Solución:

Para n = 1, tenemos a _n = a ₁ + (1 – 1) d = a ₁ , por lo que la fórmula es cierta para n = 1,

Supongamos que la fórmula a _k = a ₁ + (k – 1) es verdadera para todos los números naturales.

Ahora probaremos que la fórmula también es cierta para k+1, así que ahora tenemos,

una _{k + 1} = una ₁ + [(k + 1) – 1] re = una ₁ + k · re.

Asumimos que a _k = a ₁ + (k – 1) d, y por la definición de una secuencia aritmética a _{k+ 1} – a _k = d,

entonces, _{ak + 1} – _ak

= (a ₁ + k · d) – (a1 + (k – 1)d)

= un ₁ – un ₁ + kd – kd + d

= re

Por tanto, la fórmula es verdadera para k + 1, siempre que lo sea para k. E inicialmente demostramos que la fórmula es verdadera para n = 1. Por lo tanto, la fórmula es verdadera para todos los números naturales.

Publicación traducida automáticamente

Artículo escrito por krm24 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Ejemplos

Deja una respuesta Cancelar la respuesta