Probabilidad de distribuir M artículos entre X bolsas tal que la primera bolsa contenga N artículos

Dados tres enteros N , M , X . La tarea es encontrar la probabilidad de distribuir M elementos entre X bolsas de modo que la primera bolsa contenga N elementos
. Ejemplos: 
 

Entrada: M = 7, X =3, N = 3 
Salida: 0.2 
El número de formas de guardar 7 artículos en 3 bolsas es  . 
El número de formas de guardar 4 artículos en 2 bolsas es  . Como la primera bolsa contiene 3 artículos. 
La probabilidad es  /
Entrada: M = 9, X = 3, N = 4 
Salida: 0.142857 
 

Enfoque: 
En general, el número de formas de colocar N artículos en K bolsas es  . 
 

• El número de formas de guardar M artículos en X bolsas es  .
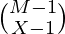• El número de formas de guardar artículos (MN) en bolsas (X-1) es  . Como la primera bolsa contiene N artículos.
• La probabilidad es  / .

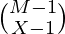A continuación se muestra la implementación del enfoque anterior:
 

// CPP program to find probability of
// first bag to contain N items such
// that M items are distributed among X bags
#include <bits/stdc++.h>
using namespace std;
 
// Function to find factorial of a number
int factorial(int n)
{
    if (n <= 1)
        return 1;
    return n * factorial(n - 1);
}
 
// Function to find nCr
int nCr(int n, int r)
{
    return factorial(n) / (factorial(r) * factorial(n - r));
}
 
// Function to find probability of
// first bag to contain N items such
// that M items are distributed among X bags
float Probability(int M, int N, int X)
{
    return (float)(nCr(M - N - 1, X - 2) /
                    (nCr(M - 1, X - 1) * 1.0));
}
 
// Driver code
int main()
{
    int M = 9, X = 3, N = 4;
 
    // Function call
    cout << Probability(M, N, X);
 
    return 0;
}

// Java program to find probability of
// first bag to contain N items such
// that M items are distributed among X bags
 
class GFG
{
 
    // Function to find factorial of a number
    public static int factorial(int n)
    {
        if (n <= 1)
            return 1;
 
        return n * factorial(n - 1);
    }
 
    // Function to find nCr
    public static int nCr(int n, int r)
    {
        return factorial(n) / (factorial(r) * factorial(n - r));
    }
 
    // Function to find probability of
    // first bag to contain N items such
    // that M items are distributed among X bags
    public static float Probability(int M, int N, int X)
    {
        return (float) (nCr(M - N - 1, X - 2) / (nCr(M - 1, X - 1) * 1.0));
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int M = 9, X = 3, N = 4;
 
        // Function call
        System.out.println(Probability(M, N, X));
    }
}
 
// This code is contributed by
// sanjeev2552

# Python3 program to find probability of
# first bag to contain N items such
# that M items are distributed among X bags
 
# Function to find factorial of a number
def factorial(n) :
 
    if (n <= 1) :
        return 1;
         
    return n * factorial(n - 1);
 
# Function to find nCr
def nCr(n, r) :
 
    return (factorial(n) / (factorial(r) *
                            factorial(n - r)));
 
# Function to find probability of
# first bag to contain N items such
# that M items are distributed among X bags
def Probability(M, N, X) :
 
    return float(nCr(M - N - 1, X - 2) /
                (nCr(M - 1, X - 1) * 1.0));
 
# Driver code
if __name__ == "__main__" :
 
    M = 9; X = 3; N = 4;
 
    # Function call
    print(Probability(M, N, X));
 
# This code is contributed by AnkitRai01

// C# program to find probability of
// first bag to contain N items such
// that M items are distributed among X bags
using System;
 
class GFG
{
  
    // Function to find factorial of a number
    static int factorial(int n)
    {
        if (n <= 1)
            return 1;
  
        return n * factorial(n - 1);
    }
  
    // Function to find nCr
    static int nCr(int n, int r)
    {
        return factorial(n) / (factorial(r) * factorial(n - r));
    }
  
    // Function to find probability of
    // first bag to contain N items such
    // that M items are distributed among X bags
    static float Probability(int M, int N, int X)
    {
        return (float) (nCr(M - N - 1, X - 2) / (nCr(M - 1, X - 1) * 1.0));
    }
  
    // Driver code
    static void Main()
    {
        int M = 9, X = 3, N = 4;
  
        // Function call
        Console.WriteLine(Probability(M, N, X));
    }
}
  
// This code is contributed by
// mohitkumar 29

<script>
// Java Script program to find probability of
// first bag to contain N items such
// that M items are distributed among X bags
 
 
    // Function to find factorial of a number
    function factorial( n)
    {
        if (n <= 1)
            return 1;
 
        return n * factorial(n - 1);
    }
 
    // Function to find nCr
    function nCr( n,  r)
    {
        return factorial(n) / (factorial(r) * factorial(n - r));
    }
 
    // Function to find probability of
    // first bag to contain N items such
    // that M items are distributed among X bags
    function Probability(M,N,X)
    {
        return parseFloat(nCr(M - N - 1, X - 2) / (nCr(M - 1, X - 1) * 1.0));
    }
 
    // Driver code
    let M = 9, X = 3, N = 4;
 
        // Function call
        document.write(Probability(M, N, X).toFixed(6));
// This code is contributed by Bobby
</script>

0.142857