El problema de transporte es un tipo especial de problema de programación lineal (LPP) en el que los bienes se transportan desde un conjunto de fuentes a un conjunto de destinos sujetos a la oferta y la demanda de las fuentes y el destino, respectivamente, de modo que se minimiza el costo total de transporte. A veces también se le llama problema de Hitchcock.
Tipos de problemas de transporte:
Equilibrado: cuando tanto la oferta como la demanda son iguales, se dice que el problema es un problema de transporte equilibrado.
Desequilibrado: cuando la oferta y la demanda no son iguales, se dice que es un problema de transporte desequilibrado. En este tipo de problema, se agrega una fila ficticia o una columna ficticia de acuerdo con el requisito para que sea un problema equilibrado. Entonces se puede resolver de manera similar al problema balanceado.
Métodos para resolver:
Para encontrar la solución factible básica inicial existen tres métodos:
- Método de la celda de la esquina noroeste.
- Método de celda de llamada mínima.
- Método de aproximación de Vogel (VAM).
Estructura básica del problema de transporte: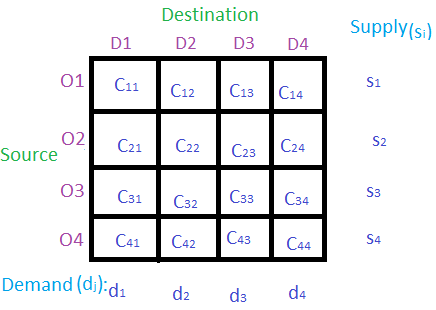
En la tabla anterior, D1 , D2 , D3 y D4 son los destinos donde los productos/mercancías se entregarán desde diferentes fuentes S1 , S2 , S3 y S4 . S i es el suministro de la fuente O i . d j es la demanda del destino D j . C ij es el costo cuando el producto se entrega desde el origen S i al destino D j .
Publicación traducida automáticamente
Artículo escrito por mkumarchaudhary06 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA