problema de transporte | Conjunto 7 (Problema de degeneración en el transporte)

Lea primero este artículo .
Este artículo discutirá la degeneración en el problema del transporte a través de un ejemplo explicado.

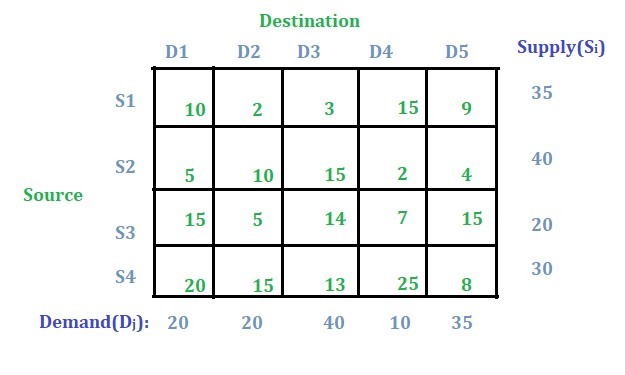
Solución:
Este problema es un problema de transporte equilibrado ya que la oferta total es igual a la demanda total.

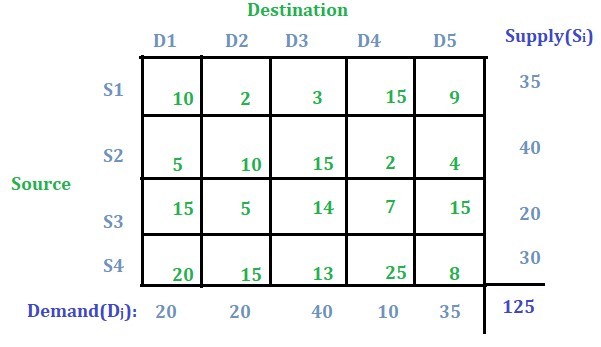
Solución factible básica inicial: Aquí se utilizará el
método de celda de menor costo para encontrar la solución factible básica inicial. También se puede usar el método de la esquina noroeste o el método de aproximación de Vogel para encontrar la solución factible básica inicial.

Usando el método de celda de menor costo , obtenemos la siguiente solución.

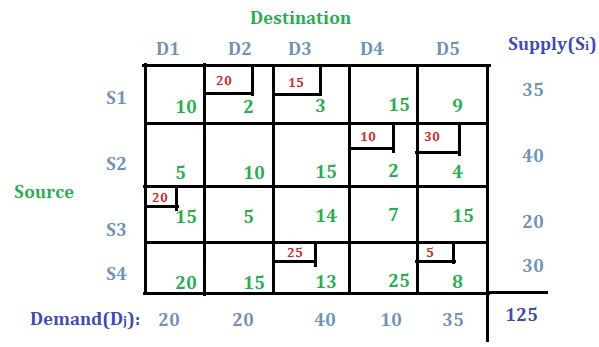
Optimización de la solución usando el Método UV:
Compruebe si m + n – 1 = número total de celdas asignadas. En este caso, m + n – 1 = 4 + 5 – 1 = 8, donde el número total de celdas asignadas es 7, por lo tanto, este es el caso de la degeneración en el problema del transporte. Entonces, en este caso, convertimos el número necesario (en este caso es m + n – 1 – número total de celdas asignadas, es decir, 8 – 7 = 1) de celdas no asignadas en celdas asignadas para satisfacer la condición anterior.

Pasos para convertir celdas no asignadas en celdas asignadas:

• Comience desde el valor mínimo de la celda no asignada.
• Verifique la formación de bucles uno por uno.
• No debe haber formación de circuito cerrado.
• Seleccione ese bucle como una nueva celda asignada y asigne un valor ‘e’.

El ciclo cerrado puede tener cualquier forma, pero todos los puntos de inflexión deben ser solo en la celda asignada o en la celda desde la que se inicia el ciclo.

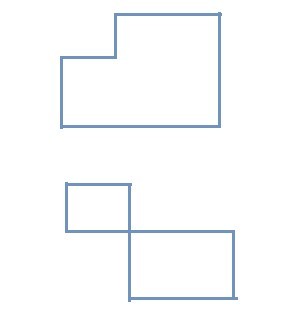
Hay 13 celdas sin asignar. Seleccione el valor mínimo (es decir, 5 en este caso) de las celdas no asignadas. Aquí hay dos 5, por lo que puede seleccionar cualquiera al azar. Seleccionemos la celda con la estrella marcada.

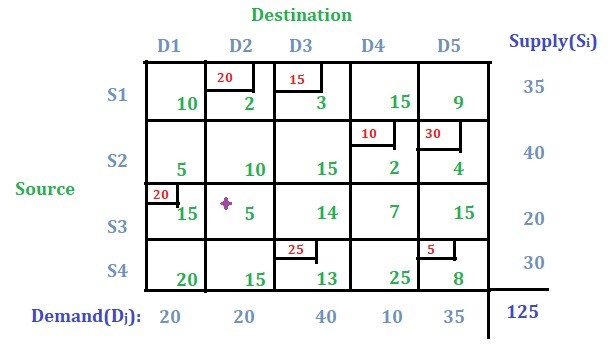
Compruebe si hay alguna formación de bucle cerrado a partir de esta celda. Si se extrae un bucle cerrado de esta celda siguiendo la condición de bucle cerrado, se puede observar que no se puede alcanzar esta celda para completar el bucle cerrado. Entonces, esta celda se seleccionará y se le asignará un valor aleatorio ‘e’.

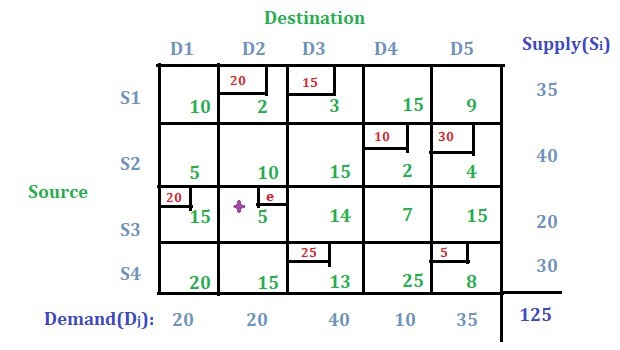
Nota: Si el ciclo cerrado se hubiera formado a partir de esa celda, probaríamos con otra celda con el valor más bajo y haríamos el mismo procedimiento y verificaríamos si el ciclo cerrado es posible o no.

Ahora el número total de celdas asignadas se convierte en 8 y m + n – 1 = 4 + 5 – 1 = 8. Ahora esta solución se puede optimizar utilizando el método UV . Obtenemos la siguiente solución después de realizar la optimización utilizando el método UV.

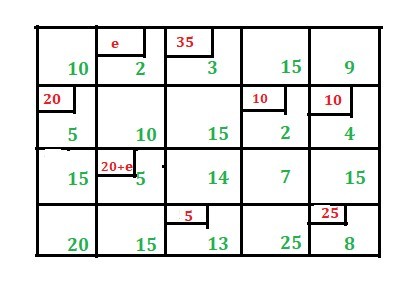
La presencia de dos ‘e’ en la solución final significa que después de hacer algunas iteraciones durante la optimización, la condición de degeneración se cumplirá una vez más.

Mientras encuentra el costo total, simplemente deje la ‘e’ y multiplique el valor asignado con el valor del costo de su celda y súmelos todos. Entonces, el costo de transporte es (35 * 3) + (20 * 5) + (10 * 2) + (10 * 4) + (20 * 5) + (5 * 13) + (25 * 8) = 630 .