Para aprender sobre Backpropagation , primero tenemos que entender la arquitectura de la red neuronal y luego el proceso de aprendizaje en ANN. Entonces, comencemos por conocer las diversas arquitecturas de ANN:
ANN es un sistema computacional que consta de muchas unidades interconectadas llamadas neuronas artificiales . La conexión entre neuronas artificiales puede transmitir una señal de una neurona a otra. Por lo tanto, existen múltiples posibilidades para conectar las neuronas en función de la arquitectura que vamos a adoptar para una solución específica. Algunas permutaciones y combinaciones son las siguientes:
- Puede haber solo dos capas de neuronas en la red: la capa de entrada y la de salida.
- Puede haber una o más capas intermedias «ocultas» de una neurona.
- Las neuronas pueden estar conectadas con todas las neuronas en la siguiente capa y así sucesivamente…
Entonces, comencemos hablando de las diversas arquitecturas posibles:
A. Red de avance de una sola capa:

Es la arquitectura más simple y básica de ANN. Consta de solo dos capas: la capa de entrada y la capa de salida. La capa de entrada consta de ‘m’ neuronas de entrada conectadas a cada una de las ‘n’ neuronas de salida. Las conexiones soportan pesos w 11 y así sucesivamente. La capa de entrada de las neuronas no realiza ningún procesamiento: pasan las señales i/p a las neuronas o/p. Los cálculos se realizan en la capa de salida. Entonces, aunque tiene 2 capas de neuronas, solo una capa realiza el cálculo. Esta es la razón por la cual la red se conoce como capa ÚNICA. Además, las señales siempre fluyen desde la capa de entrada a la capa de salida. Por lo tanto, la red se conoce como FEED FORWARD.
La entrada de señal neta a las neuronas de salida viene dada por:
![]()
La salida de señal de cada neurona de salida dependerá de la función de activación utilizada.
B. Red de avance de múltiples capas:

Red de avance de múltiples capas
La red de alimentación directa de múltiples capas es bastante similar a la red de alimentación directa de una sola capa, excepto por el hecho de que hay una o más capas intermedias de neuronas entre la capa de entrada y la de salida. Por lo tanto, la red se denomina multicapa. Cada una de las capas puede tener un número variable de neuronas. Por ejemplo, el que se muestra en el diagrama anterior tiene neuronas ‘m’ en la capa de entrada y neuronas ‘r’ en la capa de salida y solo hay una capa oculta con neuronas ‘n’.
![]()
para la k-ésima neurona de capa oculta. La entrada de señal neta a la neurona en la capa de salida viene dada por:
![]()
C. Red Competitiva:
Es igual que la red de avance de una sola capa en estructura. La única diferencia es que las neuronas de salida están conectadas entre sí (parcial o totalmente) . A continuación se muestra el diagrama para este tipo de red.

Red Competitiva
De acuerdo con el diagrama, está claro que pocas de las neuronas de salida están interconectadas entre sí. Para una entrada dada, las neuronas de salida compiten entre sí para representar la entrada. Representa una forma de algoritmo de aprendizaje no supervisado en ANN que es adecuado para encontrar los grupos en un conjunto de datos.
D. Red Recurrente:

Red recurrente
En las redes feed-forward, la señal siempre fluye desde la capa de entrada hacia la capa de salida (solo en una dirección). En el caso de las redes neuronales recurrentes, existe un bucle de retroalimentación (desde las neuronas de la capa de salida hasta las neuronas de la capa de entrada). También puede haber bucles automáticos.
El proceso de aprendizaje en ANN depende principalmente de cuatro factores, ellos son:
- El número de capas en la red (capa única o multicapa)
- Dirección del flujo de la señal (Feedforward o recurrente)
- Número de Nodes en las capas: el número de Nodes en la capa de entrada es igual al número de características del conjunto de datos de entrada. El número de Nodes de salida dependerá de los posibles resultados, es decir, el número de clases en caso de aprendizaje supervisado. Pero el número de capas en la capa oculta debe ser elegido por el usuario. Una mayor cantidad de Nodes en la capa oculta, mayor rendimiento, pero demasiados Nodes pueden resultar en un sobreajuste y en un mayor gasto computacional.
- Peso de los Nodes interconectados: Decidir el valor de los pesos asociados con cada interconexión entre cada neurona para que un problema de aprendizaje específico pueda resolverse correctamente es un problema bastante difícil en sí mismo. Tome un ejemplo para entender el problema. Tomemos el ejemplo de una red de avance de múltiples capas, tenemos que entrenar un modelo ANN usando algunos datos, para que pueda clasificar un nuevo conjunto de datos, digamos p_5(3,-2). Digamos que hemos deducido que p_1=(5,2) y p_2 = (-1,12) pertenecientes a la clase C1 mientras que p_3=(3,-5) y p_4 = (-2,-1) pertenecientes a la clase C2. Asumimos los valores de los pesos sinápticos w_0,w_1,w_2 como -2, 1/2 y 1/4 respectivamente. Pero NO obtendremos estos valores de peso para cada problema de aprendizaje. Para resolver un problema de aprendizaje con ANN, podemos comenzar con un conjunto de valores para los pesos sinápticos y seguir cambiándolos en múltiples iteraciones. El criterio de parada puede ser la tasa de clasificación errónea < 1 % o el número máximo de iteraciones debe ser inferior a 25 (un valor umbral). Puede haber otro problema: la tasa de clasificación errónea puede no reducirse progresivamente.
Entonces, podemos resumir el proceso de aprendizaje en ANN como la combinación de: decidir la cantidad de capas ocultas, la cantidad de Nodes en cada una de las capas ocultas, la dirección del flujo de la señal, decidir el peso de la conexión.
La red de alimentación multicapa es una arquitectura de uso común. Se ha observado que una red neuronal con incluso una capa oculta se puede utilizar para aproximar razonablemente cualquier función continua. La metodología de aprendizaje adoptada para entrenar una red feed-forward multicapa es Backpropagation .
Retropropagación:
En la sección anterior, sabemos que las actividades más críticas del entrenamiento de una ANN son asignar los pesos de conexión entre neuronas. En 1986, se introdujo una forma eficiente de entrenar una ANN. En este método, la diferencia en los valores de salida de la capa de salida y los valores esperados se propagan desde la capa de salida a las capas precedentes . Por lo tanto, el algoritmo que implementa este método se conoce como BACK PROPAGATION, es decir, propaga los errores de vuelta a las capas anteriores .
El algoritmo de retropropagación es aplicable para la red de avance de múltiples capas. Es un algoritmo de aprendizaje supervisado que continúa ajustando los pesos de las neuronas conectadas con el objetivo de reducir la desviación de la señal de salida de la salida objetivo. Este algoritmo consta de múltiples iteraciones, conocidas como épocas. Cada época consta de dos fases:
- Fase directa: flujo de señal desde las neuronas en la capa de entrada a las neuronas en la capa de salida a través de las capas ocultas. Los pesos de las interconexiones y funciones de activación se utilizan durante el flujo. En la capa de salida, se generan las señales de salida.
- Fase hacia atrás: la señal se compara con el valor esperado. Los errores calculados se propagan hacia atrás desde la salida a la capa anterior. El error propagado hacia atrás se utiliza para ajustar los pesos de interconexión entre las capas.

PROPAGACIÓN HACIA ATRÁS
El diagrama anterior muestra una versión razonablemente simplificada del algoritmo de propagación hacia atrás.
Una parte principal del algoritmo es ajustar los pesos de interconexión. Esto se hace usando una técnica denominada Descenso de Gradiente . En palabras simples, el algoritmo calcula la derivada parcial de la función de activación por cada peso de interconexión para identificar el ‘gradiente’ o el grado de cambio del peso requerido para minimizar la función de costo.
Para comprender el algoritmo de propagación hacia atrás en detalle, consideremos la red de alimentación hacia adelante de múltiples capas.

La entrada de señal neta a las neuronas de la capa oculta viene dada por:
![]()
Si ![]() es la función de activación de la capa oculta, entonces
es la función de activación de la capa oculta, entonces ![]()
La entrada de señal neta a las neuronas de la capa de salida viene dada por:
![]()

RED DE PROPAGACIÓN HACIA ATRÁS
Tenga en cuenta que se supone que las señales ![]() y
y ![]() son 1. Si
son 1. Si ![]() es la función de activación de la capa oculta, entonces
es la función de activación de la capa oculta, entonces ![]()
Si es el objetivo de la k-ésima neurona de salida, entonces la función de costo definida como el error cuadrático de la capa de salida está dada por:
![]()
![]()
De acuerdo con el algoritmo de descenso , se debe tomar la derivada parcial de la función de costo E con respecto a los pesos de interconexión. Matemáticamente se puede representar como:
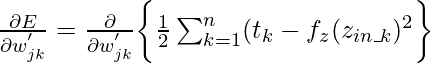
{La expresión anterior es para los pesos de interconexión entre la j-ésima neurona en la capa oculta y la k-ésima neurona en la capa de salida .} Esta expresión se puede reducir a
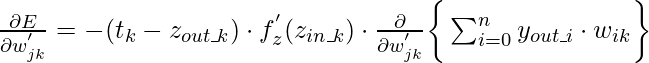
donde, ![]() o
o ![]()
Si asumimos ![]() como componente del ajuste de peso necesario para el peso
como componente del ajuste de peso necesario para el peso ![]() correspondiente a la k-ésima neurona de salida, entonces:
correspondiente a la k-ésima neurona de salida, entonces:
![]()
Sobre esta base, los pesos y el sesgo deben actualizarse de la siguiente manera:
- Para pesos:
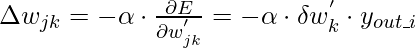
- Por eso,
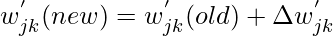
- Por sesgo:
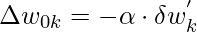
- Por eso,
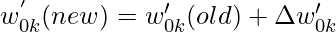
En las expresiones anteriores, alfa es la tasa de aprendizaje de la red neuronal. La tasa de aprendizaje es un parámetro de usuario que disminuye o aumenta la velocidad con la que se ajustarán los pesos de interconexión de una red neuronal. Si la tasa de aprendizaje es demasiado alta, el ajuste realizado como parte del proceso de descenso de gradiente puede divergir el conjunto de datos en lugar de converger. Por otro lado, si la tasa de aprendizaje es demasiado baja, la optimización puede consumir más tiempo debido a los pequeños pasos hacia los mínimos.
{Todos los cálculos anteriores son para el peso de interconexión entre las neuronas en la capa oculta y las neuronas en la capa de salida}
Al igual que las expresiones anteriores, podemos deducir las expresiones para “Pesos de interconexión entre las capas de entrada y ocultas:
- Para pesos:
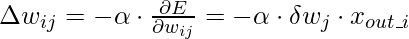
- Por eso,
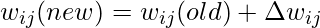
- Por sesgo:
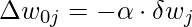
- Por eso,
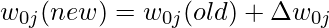
Entonces, de esta manera, podemos usar el algoritmo Backpropagation para resolver varias Redes Neuronales Artificiales.
Publicación traducida automáticamente
Artículo escrito por versatile1990 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA