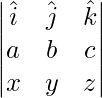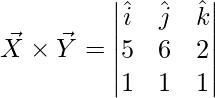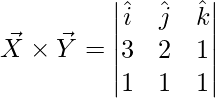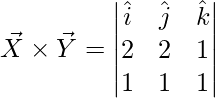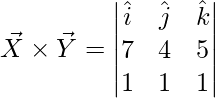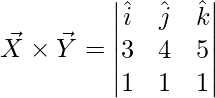Producto cruzado de dos vectores

El vector es una entidad bidimensional con magnitud y dirección. Un vector se puede ver geométricamente como un segmento de línea dirigido con una flecha que indica la dirección y una longitud igual a la magnitud del vector. La dirección del vector es de la cola a la cabeza. Si dos vectores tienen la misma magnitud y dirección, son iguales. Esto indica que si tomamos un vector y lo trasladamos a un nuevo punto (sin rotarlo), el vector que obtenemos al final es el mismo con el que comenzamos.

Producto cruzado de dos vectores

En el espacio tridimensional, el producto cruz es una operación binaria en dos vectores. Genera un vector perpendicular a ambos vectores dados. a × b representa el producto vectorial de dos vectores, a y b. Produce un vector que es perpendicular tanto a a como a b. Los productos cruzados son otro nombre para los productos vectoriales. El resultado del producto vectorial de dos vectores es un vector, que puede determinarse mediante la regla de la mano derecha.

a × b = |a||b|senθ

Array de productos cruzados

También podemos derivar la fórmula para el producto cruzado de dos vectores usando el determinante de la array como se indica a continuación.

A = ai + bj + ck

B = xi + yj + zk

A × B = $\begin{vmatrix}{\hat{i}}&{\hat{j}}&{\hat{k}}\\a&b&c\\x&y&z\end{vmatrix}$

= $(bz - cy)\hat{i} - (az - cx){j} + (ay - bx){k}$

= (bz – cy)i + (cx – az)j + (ay – bx)k

Problemas de muestra

Pregunta 1. Encuentra el producto cruz de los vectores: $\vec{X}=5\hat{i}+6\hat{j}+2\hat{k}$ y $\vec{Y}= \hat{i} + \hat{j} + \hat{k}.$

Solución:

Dado: $\vec{X}=5\hat{i}+6\hat{j}+2\hat{k} and \vec{Y}= \hat{i} + \hat{j} + \hat{k}.$

$\vec{X}\times \vec{Y} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ 5 & 6 & 2\\ 1 & 1 & 1 \end{vmatrix}$

$\vec{X}\times \vec{Y}= (6-2)\hat{i}-(5-2)\hat{j}+ (5-6)\hat{k}$

$\vec{X}\times \vec{Y}= 4\vec{i}-3\vec{j}- \vec{k}$

Pregunta 2. Encuentra el producto cruz de los vectores: $\vec{X}=3\hat{i}+2\hat{j}+1\hat{k}and\vec{Y}=\hat{i}+\hat{j}+\hat{k}.$

Solución:

Dado: $\vec{X}=3\hat{i}+2\hat{j}+1\hat{k}and\vec{Y}=\hat{i}+\hat{j}+\hat{k}$ .

$\vec{X}\times \vec{Y} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ 3 & 2 & 1\\ 1 & 1 & 1 \end{vmatrix}$

$\vec{X}\times \vec{Y}= \vec{i}-2\vec{j}+ \vec{k}$

Pregunta 3. Encuentra el producto cruz de los vectores: $\vec{X}=2\hat{i}+2\hat{j}+1\hat{k}$ y $\vec{Y}=\hat{i}+\hat{j}+\hat{k}$ .

Solución:

Dado: $\vec{X}=2\hat{i}+2\hat{j}+1\hat{k}$ y $\vec{Y}=\hat{i}+\hat{j}+\hat{k}$ .

$\vec{X}\times \vec{Y} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ 2 & 2 & 1\\ 1 & 1 & 1 \end{vmatrix}$

$\vec{X}\times \vec{Y}= \vec{i}-\vec{j}+ 0\vec{k}$

Pregunta 4. Encuentra el producto cruz de los vectores: $\vec{X}=2\hat{i}+2\hat{j}+5\hat{k}$ y $\vec{Y}=\hat{i}+\hat{j}+\hat{k}$ .

Solución:

Dado: $\vec{X}=2\hat{i}+2\hat{j}+2\hat{k} and \vec{Y}=\hat{i}+\hat{j}+\hat{k}$ .

$\vec{X}\times \vec{Y} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ 2 & 2 & 5\\ 1 & 1 & 1 \end{vmatrix}$

$\vec{X}\times \vec{Y}= -3\vec{i}+3\vec{j}+ 0\vec{k}$

Pregunta 5. Encuentra el producto cruz de los vectores: $\vec{X}=7\hat{i}+6\hat{j}+5\hat{k}$ y $\vec{Y}=\hat{i}+\hat{j}+\hat{k}$ .

Solución:

Dado: $\vec{X}=7\hat{i}+6\hat{j}+5\hat{k}$ y $\vec{Y}=\hat{i}+\hat{j}+\hat{k}.$

$\vec{X}\times \vec{Y} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ 7 & 6 & 5\\ 1 & 1 & 1 \end{vmatrix}$

$\vec{X}\times \vec{Y}= \vec{i}-2\vec{j}+ \vec{k}$

Pregunta 5. Encuentra el producto cruz de los vectores: $\vec{X}=7\hat{i}+4\hat{j}+5\hat{k}$ y $\vec{Y}=\hat{i}+\hat{j}+\hat{k}$ .

Solución:

Dado: $\vec{X}=7\hat{i}+4\hat{j}+5\hat{k}$ y $\vec{Y}=\hat{i}+\hat{j}+\hat{k}$ .

$\vec{X}\times \vec{Y} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ 7 & 4 & 5\\ 1 & 1 & 1 \end{vmatrix}$

$\vec{X}\times \vec{Y}= -\vec{i}-2\vec{j}+ 3\vec{k}$

Pregunta 6. Encuentra el producto cruz de los vectores: $\vec{X}=3\hat{i}+4\hat{j}+5\hat{k}$ y $\vec{Y}=\hat{i}+\hat{j}+\hat{k}$ .

Solución:

Dado: $\vec{X}=3\hat{i}+4\hat{j}+5\hat{k}$ y $\vec{Y}=\hat{i}+\hat{j}+\hat{k}$ .

$\vec{X}\times \vec{Y} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ 3 & 4 & 5\\ 1 & 1 & 1 \end{vmatrix}$

$\vec{X}\times \vec{Y}= -\vec{i}+2\vec{j}-\vec{k}$

Pregunta 7. Encuentra el producto cruz de los vectores: $\vec{X}=2\hat{i}+3\hat{j}+4\hat{k}$ y $\vec{Y}=\hat{i}+\hat{j}+\hat{k}$ .

Solución:

Dado: $\vec{X}=2\hat{i}+3\hat{j}+4\hat{k}$ y $\vec{Y}=\hat{i}+\hat{j}+\hat{k}$ .

$\vec{X}\times \vec{Y} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ 2 & 3 & 4\\ 1 & 1 & 1 \end{vmatrix}$

$\vec{X}\times \vec{Y}= -\vec{i}+2\vec{j}-\vec{k}$

Publicación traducida automáticamente

Artículo escrito por parmaramolaksingh1955 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Producto cruzado de dos vectores

Problemas de muestra

Deja una respuesta Cancelar la respuesta