Programa C++ para array diagonalmente dominante

En matemáticas, se dice que una array cuadrada es diagonalmente dominante si, para cada fila de la array, la magnitud de la entrada diagonal en una fila es mayor o igual a la suma de las magnitudes de todas las demás (no diagonales). entradas en esa fila. Más precisamente, la array A es diagonalmente dominante si 
 

Por ejemplo, la array 
 

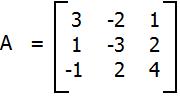
es diagonalmente dominante porque 
|a ₁₁ | ≥ |a ₁₂ | + |a ₁₃ | desde |+3| ≥ |-2| + |+1| 
|un ₂₂ | ≥ |a ₂₁ | + |a ₂₃ | desde |-3| ≥ |+1| + |+2| 
|un ₃₃ | ≥ |a ₃₁ | + |a ₃₂ | desde |+4| ≥ |-1| + |+2|
Dada una array A de n filas y n columnas. La tarea es verificar si la array A es diagonalmente dominante o no.
Ejemplos: 

Input : A = { { 3, -2, 1 },
              { 1, -3, 2 },
              { -1, 2, 4 } };
Output : YES
Given matrix is diagonally dominant
because absolute value of every diagonal
element is more than sum of absolute values
of corresponding row.

Input : A = { { -2, 2, 1 },
              { 1, 3, 2 },
              { 1, -2, 0 } };
Output : NO

La idea es ejecutar un ciclo desde i = 0 hasta n-1 para el número de filas y para cada fila, ejecutar un ciclo j = 0 hasta n-1 para encontrar la suma del elemento no diagonal, es decir, i != j. Y comprueba si el elemento de la diagonal es mayor o igual que la suma. Si para alguna fila, es falso, devuelva falso o imprima «No». De lo contrario, escriba «SÍ». 
 

A continuación se muestra la implementación del enfoque. 

// CPP Program to check whether given matrix
// is Diagonally Dominant Matrix.
#include <bits/stdc++.h>
#define N 3
using namespace std;
 
// check the given matrix is Diagonally
// Dominant Matrix or not.
bool isDDM(int m[N][N], int n)
{
    // for each row
    for (int i = 0; i < n; i++)
   {       
 
        // for each column, finding sum of each row.
        int sum = 0;
        for (int j = 0; j < n; j++)            
            sum += abs(m[i][j]);       
 
        // removing the diagonal element.
        sum -= abs(m[i][i]);
 
        // checking if diagonal element is less
        // than sum of non-diagonal element.
        if (abs(m[i][i]) < sum)
            return false;
        
    }
 
    return true;
}
 
// Driven Program
int main()
{
    int n = 3;
    int m[N][N] = { { 3, -2, 1 },
                    { 1, -3, 2 },
                    { -1, 2, 4 } };
 
    (isDDM(m, n)) ? (cout << "YES") : (cout << "NO");
 
    return 0;
}

YES

Complejidad de tiempo: O(N ² ), ya que se utilizan bucles anidados 
Espacio auxiliar: O(1)

¡ Consulte el artículo completo sobre la array diagonalmente dominante para obtener más detalles!