Programa para calcular el area de Kite

Kite es algo así como rombo pero en Kite, los lados adyacentes son iguales y las diagonales generalmente no son iguales. 
 

Método 1: cuando se dan ambas diagonales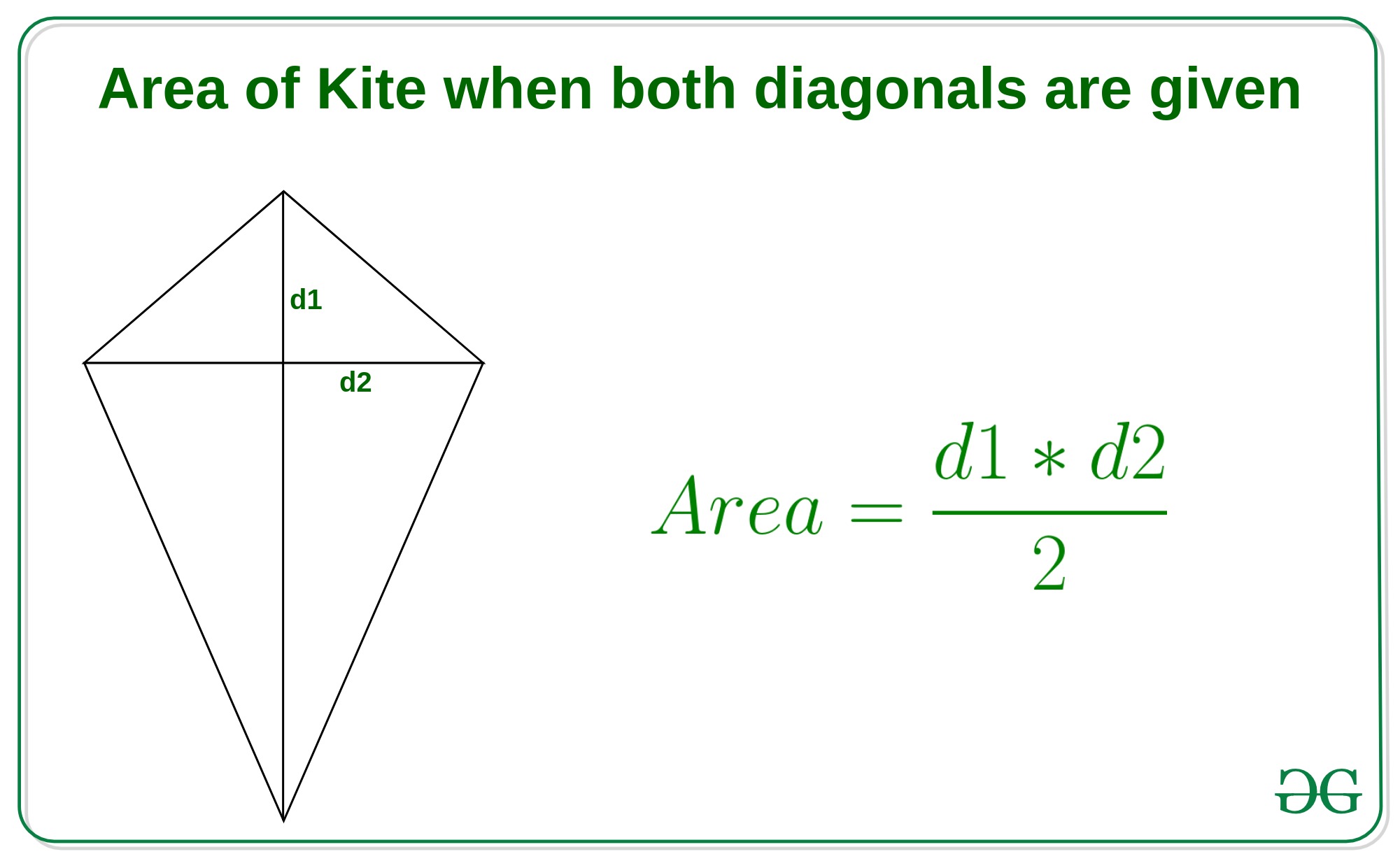

Si se dan las diagonales d1 y d2 de la cometa, entonces el área de una cometa es la mitad del producto de ambas diagonales, es decir
 

Ejemplo:
 

Input: d1 = 4, d2 = 6
Output: Area of Kite  = 12

Input: d1 = 5, d2 = 7
Output: Area of Kite  = 17.5

Enfoque: en este método simplemente usamos la fórmula anterior.
A continuación se muestra la implementación del enfoque anterior:
 

// C++ implementation of the approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to return the area of kite
float areaOfKite(int d1, int d2)
{
    // use above formula
    float area = (d1 * d2) / 2;
    return area;
}
 
// Driver code
int main()
{
    int d1 = 4, d2 = 6;
    cout << "Area of Kite = "
         << areaOfKite(d1, d2);
 
    return 0;
}

// Java implementation of the approach
class GFG
{
 
    // Function to return the area of kite
    static float areaOfKite(int d1, int d2)
    {
        // Use above formula
        float area = (d1 * d2) / 2;
        return area;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int d1 = 4, d2 = 6;
        System.out.println("Area of Kite = "
                + areaOfKite(d1, d2));
    }
}
 
// This code is contributed by Rajput-Ji

    # Python implementation of the approach
 
# Function to return the area of kite
def areaOfKite(d1, d2):
 
    # use above formula
    area = (d1 * d2) / 2;
    return area;
 
# Driver code
d1 = 4;
d2 = 6;
print("Area of Kite = ",
    areaOfKite(d1, d2));
 
# This code is contributed by Rajput-Ji

// C# implementation of the approach
using System;
 
class GFG
{
 
// Function to return the area of kite
static float areaOfKite(int d1, int d2)
{
    // Use above formula
    float area = (d1 * d2) / 2;
    return area;
}
 
// Driver code
public static void Main()
{
    int d1 = 4, d2 = 6;
    Console.WriteLine("Area of Kite = "
            + areaOfKite(d1, d2));
}
}
 
// This code is contributed by anuj_67..

<script>
 
// Javascript implementation of the approach
 
// Function to return the area of kite
function areaOfKite(d1, d2)
{
    // use above formula
    var area = (d1 * d2) / 2;
    return area;
}
 
// Driver code
var d1 = 4, d2 = 6;
document.write("Area of Kite = "
    + areaOfKite(d1, d2));
 
</script>

Area of Kite = 12

Complejidad de tiempo: O(1)

Espacio Auxiliar: O(1)

Método 2: Cuando se dan los lados a, b y el ángulo: 
 
Cuando se dan los lados desiguales de la cometa a y b y el ángulo Θ incluido entre ellos, entonces 
 

Ejemplo: 
 

Input: a = 4, b = 7, θ = 78
Output: Area of Kite  = 27.3881

Input: a = 6, b = 9, θ = 83
Output: Area of Kite  = 53.5975

Enfoque: en este método simplemente usamos la fórmula anterior.
A continuación se muestra la implementación del enfoque anterior:
 

// C++ implementation of the approach
 
#include <bits/stdc++.h>
#define PI 3.14159 / 180
using namespace std;
 
// Function to return the area of the kite
float areaOfKite(int a, int b, double angle)
{
    // convert angle degree to radians
    angle = angle * PI;
    // use above formula
 
    double area = a * b * sin(angle);
    return area;
}
 
// Driver code
int main()
{
    int a = 4, b = 7, angle = 78;
    cout << "Area of Kite = "
         << areaOfKite(a, b, angle);
 
    return 0;
}

// Java implementation of the approach
import java.io.*;
 
class GFG
{
     
static double PI = (3.14159 / 180);
 
// Function to return the area of the kite
static float areaOfKite(int a, int b, double angle)
{
    // convert angle degree to radians
    angle = angle * PI;
     
    // use above formula
    double area = a * b * Math.sin(angle);
    return (float)area;
}
 
// Driver code
public static void main (String[] args)
{
 
    int a = 4, b = 7, angle = 78;
    System.out.println ("Area of Kite = " + areaOfKite(a, b, angle));
}
}
 
// This code is contributed by jit_t.

# Python implementation of the approach
import math
PI = 3.14159 / 180;
 
# Function to return the area of the kite
def areaOfKite(a, b, angle):
     
    # convert angle degree to radians
    angle = angle * PI;
     
    # use above formula
 
    area = a * b * math.sin(angle);
    return area;
 
# Driver code
a = 4; b = 7; angle = 78;
print("Area of Kite = ",
        areaOfKite(a, b, angle));
 
# This code contributed by PrinciRaj1992

// C# implementation of the approach
using System;
 
class GFG
{
    static double PI = (3.14159 / 180);
 
// Function to return the area of the kite
static float areaOfKite(int a, int b, double angle)
{
    // convert angle degree to radians
    angle = angle * PI;
     
    // use above formula
    double area = a * b * Math.Sin(angle);
    return (float)area;
}
 
// Driver code
static public void Main ()
{
    int a = 4, b = 7, angle = 78;
    Console.WriteLine("Area of Kite = " + areaOfKite(a, b, angle));
}
}
 
// This code is contributed by ajit

<script>
// Javascript implementation of the approach
var PI = 3.14159 / 180
 
// Function to return the area of the kite
function areaOfKite(a, b, angle)
{
 
    // convert angle degree to radians
    angle = angle * PI;
    // use above formula
 
    var area = a * b * Math.sin(angle);
    return area.toFixed(4);
}
 
// Driver code
var a = 4, b = 7, angle = 78;
document.write( "Area of Kite = "
     + areaOfKite(a, b, angle));
 
// This code is contributed by rutvik_56.
</script>

Area of Kite = 27.3881

Complejidad de tiempo: O(1)

Espacio Auxiliar: O(1)