Programa para calcular Raíz Cuadrada Media

Dada una array de N números. La tarea es calcular la Raíz Cuadrada Media (RMS) de los números dados. 
Ejemplos : 
 

Input: arr[] = {1, 2, 3, 4, 5}
Output: 3.31662

Input: arr[] = {10, 4, 6, 8}
Output: 7.34847

Enfoque: El valor de la raíz cuadrática media de N números x1,x2,x3,…..xn se puede dar como, 
 

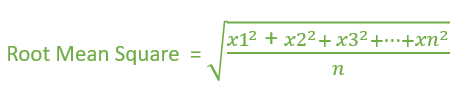
El método RMS primero calcula el cuadrado de cada número y luego calcula la media y finalmente calcula la raíz cuadrada de la media.
A continuación se muestra el programa para encontrar RMS de N números: 
 

// CPP program to calculate Root Mean Square
#include <bits/stdc++.h>
using namespace std;
 
// Function that Calculate Root Mean Square
float rmsValue(int arr[], int n)
{
    int square = 0;
    float mean = 0.0, root = 0.0;
 
    // Calculate square.
    for (int i = 0; i < n; i++) {
        square += pow(arr[i], 2);
    }
 
    // Calculate Mean.
    mean = (square / (float)(n));
 
    // Calculate Root.
    root = sqrt(mean);
 
    return root;
}
 
// Driver code
int main()
{
    int arr[] = { 10, 4, 6, 8 };
    int n = sizeof(arr) / sizeof(arr[0]);
 
    cout << rmsValue(arr, n);
 
    return 0;
}

// Java program to calculate
// Root Mean Square
 
class GFG
{
 
// Function that Calculate Root
// Mean Square
static float rmsValue(int arr[], int n)
{
    int square = 0;
    float mean = 0;
    float root = 0;
 
    // Calculate square.
    for(int i = 0; i < n; i++)
    {
        square += Math.pow(arr[i], 2);
    }
     
    // Calculate Mean.
    mean = (square / (float) (n));
 
    // Calculate Root.
    root = (float)Math.sqrt(mean);
 
    return root;
}
 
 
// Driver Code
public static void main(String args[])
{
    int arr[] = { 10, 4, 6, 8};
     
    int n = arr.length;
     
    System.out.println(rmsValue(arr, n));
}
}
 
// This code is contributed by ANKITRAI1

#Python3 program to calculate Root Mean Square
 
import math
#Function that Calculate Root Mean Square
def rmsValue(arr, n):
    square = 0
    mean = 0.0
    root = 0.0
     
    #Calculate square
    for i in range(0,n):
        square += (arr[i]**2)
     
    #Calculate Mean
    mean = (square / (float)(n))
     
    #Calculate Root
    root = math.sqrt(mean)
     
    return root
 
#Driver code
if __name__=='__main__':
    arr = [10, 4, 6, 8]
    n = len(arr)
    print(rmsValue(arr, n))
 
#This code is contributed by Shashank_Sharma

// C# program to calculate
// Root Mean Square
using System;
class GFG
{
 
// Function that Calculate
// Root Mean Square
static float rmsValue(int[] arr, int n)
{
    int square = 0;
    float mean = 0;
    float root = 0;
 
    // Calculate square.
    for(int i = 0; i < n; i++)
    {
        square += (int)Math.Pow(arr[i], 2);
    }
     
    // Calculate Mean.
    mean = (square / (float) (n));
 
    // Calculate Root.
    root = (float)Math.Sqrt(mean);
 
    return root;
}
 
// Driver Code
public static void Main()
{
    int[] arr = {10, 4, 6, 8};
     
    int n = arr.Length;
     
    Console.Write(rmsValue(arr, n));
}
}
 
// This code is contributed
// by ChitraNayal

<?php
// PHP program to calculate Root
// Mean Square
 
// Function that Calculate Root
// Mean Square
function rmsValue($arr, $n)
{
    $square = 0;
    $mean = 0.0;
    $root = 0.0;
 
    // Calculate square.
    for ($i = 0; $i < $n; $i++)
    {
        $square += pow($arr[$i], 2);
    }
 
    // Calculate Mean.
    $mean = ($square / (float)($n));
 
    // Calculate Root.
    $root = sqrt($mean);
 
    return $root;
}
 
// Driver code
$arr = array( 10, 4, 6, 8 );
$n = sizeof($arr);
 
echo rmsValue($arr, $n);
 
// This code is contributed
// by jit_t
?>

<script>
 
// javascript program to calculate
// Root Mean Square
 
    // Function that Calculate Root
    // Mean Square
    function rmsValue(arr , n) {
        var square = 0;
        var mean = 0;
        var root = 0;
 
        // Calculate square.
        for (i = 0; i < n; i++) {
            square += Math.pow(arr[i], 2);
        }
 
        // Calculate Mean.
        mean = (square /  (n));
 
        // Calculate Root.
        root =  Math.sqrt(mean);
 
        return root;
    }
 
    // Driver Code
     
        var arr = [ 10, 4, 6, 8 ];
 
        var n = arr.length;
 
        document.write(rmsValue(arr, n).toFixed(5));
 
// This code contributed by aashish1995
 
</script>

7.34847

Complejidad de tiempo: O(log(n) + sqrt(n))
Espacio auxiliar: O(1)