Prerrequisito: eliminación de Gauss para resolver ecuaciones lineales
Introducción: el método de Gauss-Jordan, también conocido como método de eliminación de Gauss-Jordan, se utiliza para resolver un sistema de ecuaciones lineales y es una versión modificada del método de eliminación de Gauss .
Es similar y más simple que el Método de eliminación de Gauss, ya que tenemos que realizar 2 procesos diferentes en el Método de eliminación de Gauss, es decir,
1) Formación de la array triangular superior y
2) Sustitución hacia atrás.
Pero en el caso del Método de eliminación de Gauss-Jordan, solo tenemos que formar una forma escalonada de fila reducida (array diagonal). A continuación se muestra el diagrama de flujo del método de eliminación de Gauss-Jordan.
Diagrama de flujo del método de eliminación de Gauss-Jordan:

Ejemplos:
Input : 2y + z = 4
x + y + 2z = 6
2x + y + z = 7
Output :
Final Augmented Matrix is :
1 0 0 2.2
0 2 0 2.8
0 0 -2.5 -3
Result is : 2.2 1.4 1.2
Explicación: A continuación se proporciona la explicación del ejemplo anterior.
- La array aumentada de entrada es:
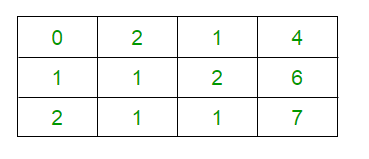
- Intercambiando R1 y R2, obtenemos
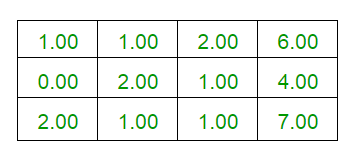
- Realizando la operación de fila R3 <- R3 – (2*R1)
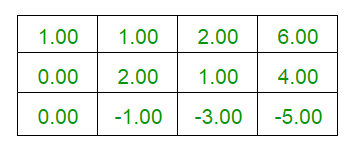
- Realizando las operaciones de fila R1 <- R1 – ((1/2)* R2) y R3 <- R3 + ((1/2)*R2)
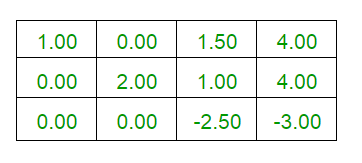
- Ejecutando R1 <- R1 + ((3/5)*R3) y R2 <- R2 + ((2/5)*R3)
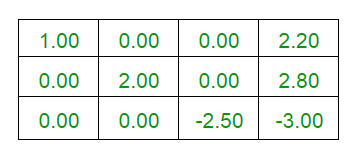
- Las Soluciones Únicas son:

C++
// C++ Implementation for Gauss-Jordan
// Elimination Method
#include <bits/stdc++.h>
using namespace std;
#define M 10
// Function to print the matrix
void PrintMatrix(float a[][M], int n)
{
for (int i = 0; i < n; i++) {
for (int j = 0; j <= n; j++)
cout << a[i][j] << " ";
cout << endl;
}
}
// function to reduce matrix to reduced
// row echelon form.
int PerformOperation(float a[][M], int n)
{
int i, j, k = 0, c, flag = 0, m = 0;
float pro = 0;
// Performing elementary operations
for (i = 0; i < n; i++)
{
if (a[i][i] == 0)
{
c = 1;
while ((i + c) < n && a[i + c][i] == 0)
c++;
if ((i + c) == n) {
flag = 1;
break;
}
for (j = i, k = 0; k <= n; k++)
swap(a[j][k], a[j+c][k]);
}
for (j = 0; j < n; j++) {
// Excluding all i == j
if (i != j) {
// Converting Matrix to reduced row
// echelon form(diagonal matrix)
float pro = a[j][i] / a[i][i];
for (k = 0; k <= n; k++)
a[j][k] = a[j][k] - (a[i][k]) * pro;
}
}
}
return flag;
}
// Function to print the desired result
// if unique solutions exists, otherwise
// prints no solution or infinite solutions
// depending upon the input given.
void PrintResult(float a[][M], int n, int flag)
{
cout << "Result is : ";
if (flag == 2)
cout << "Infinite Solutions Exists" << endl;
else if (flag == 3)
cout << "No Solution Exists" << endl;
// Printing the solution by dividing constants by
// their respective diagonal elements
else {
for (int i = 0; i < n; i++)
cout << a[i][n] / a[i][i] << " ";
}
}
// To check whether infinite solutions
// exists or no solution exists
int CheckConsistency(float a[][M], int n, int flag)
{
int i, j;
float sum;
// flag == 2 for infinite solution
// flag == 3 for No solution
flag = 3;
for (i = 0; i < n; i++)
{
sum = 0;
for (j = 0; j < n; j++)
sum = sum + a[i][j];
if (sum == a[i][j])
flag = 2;
}
return flag;
}
// Driver code
int main()
{
float a[M][M] = {{ 0, 2, 1, 4 },
{ 1, 1, 2, 6 },
{ 2, 1, 1, 7 }};
// Order of Matrix(n)
int n = 3, flag = 0;
// Performing Matrix transformation
flag = PerformOperation(a, n);
if (flag == 1)
flag = CheckConsistency(a, n, flag);
// Printing Final Matrix
cout << "Final Augmented Matrix is : " << endl;
PrintMatrix(a, n);
cout << endl;
// Printing Solutions(if exist)
PrintResult(a, n, flag);
return 0;
}
Java
// Java Implementation for Gauss-Jordan
// Elimination Method
class GFG {
static int M = 10;
// Function to print the matrix
static void PrintMatrix(float a[][], int n)
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j <= n; j++)
System.out.print(a[i][j] + " ");
System.out.println();
}
}
// function to reduce matrix to reduced
// row echelon form.
static int PerformOperation(float a[][], int n)
{
int i, j, k = 0, c, flag = 0, m = 0;
float pro = 0;
// Performing elementary operations
for (i = 0; i < n; i++)
{
if (a[i][i] == 0)
{
c = 1;
while ((i + c) < n && a[i + c][i] == 0)
c++;
if ((i + c) == n)
{
flag = 1;
break;
}
for (j = i, k = 0; k <= n; k++)
{
float temp =a[j][k];
a[j][k] = a[j+c][k];
a[j+c][k] = temp;
}
}
for (j = 0; j < n; j++)
{
// Excluding all i == j
if (i != j)
{
// Converting Matrix to reduced row
// echelon form(diagonal matrix)
float p = a[j][i] / a[i][i];
for (k = 0; k <= n; k++)
a[j][k] = a[j][k] - (a[i][k]) * p;
}
}
}
return flag;
}
// Function to print the desired result
// if unique solutions exists, otherwise
// prints no solution or infinite solutions
// depending upon the input given.
static void PrintResult(float a[][], int n, int flag)
{
System.out.print("Result is : ");
if (flag == 2)
System.out.println("Infinite Solutions Exists");
else if (flag == 3)
System.out.println("No Solution Exists");
// Printing the solution by dividing constants by
// their respective diagonal elements
else {
for (int i = 0; i < n; i++)
System.out.print(a[i][n] / a[i][i] +" ");
}
}
// To check whether infinite solutions
// exists or no solution exists
static int CheckConsistency(float a[][], int n, int flag)
{
int i, j;
float sum;
// flag == 2 for infinite solution
// flag == 3 for No solution
flag = 3;
for (i = 0; i < n; i++)
{
sum = 0;
for (j = 0; j < n; j++)
sum = sum + a[i][j];
if (sum == a[i][j])
flag = 2;
}
return flag;
}
// Driver code
public static void main(String[] args)
{
float a[][] = {{ 0, 2, 1, 4 },
{ 1, 1, 2, 6 },
{ 2, 1, 1, 7 }};
// Order of Matrix(n)
int n = 3, flag = 0;
// Performing Matrix transformation
flag = PerformOperation(a, n);
if (flag == 1)
flag = CheckConsistency(a, n, flag);
// Printing Final Matrix
System.out.println("Final Augmented Matrix is : ");
PrintMatrix(a, n);
System.out.println("");
// Printing Solutions(if exist)
PrintResult(a, n, flag);
}
}
/* This code contributed by PrinciRaj1992 */
C#
// C# Implementation for Gauss-Jordan
// Elimination Method
using System;
using System.Collections.Generic;
class GFG
{
static int M = 10;
// Function to print the matrix
static void PrintMatrix(float [,]a, int n)
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j <= n; j++)
Console.Write(a[i, j] + " ");
Console.WriteLine();
}
}
// function to reduce matrix to reduced
// row echelon form.
static int PerformOperation(float [,]a, int n)
{
int i, j, k = 0, c, flag = 0;
// Performing elementary operations
for (i = 0; i < n; i++)
{
if (a[i, i] == 0)
{
c = 1;
while ((i + c) < n && a[i + c, i] == 0)
c++;
if ((i + c) == n)
{
flag = 1;
break;
}
for (j = i, k = 0; k <= n; k++)
{
float temp = a[j, k];
a[j, k] = a[j + c, k];
a[j + c, k] = temp;
}
}
for (j = 0; j < n; j++)
{
// Excluding all i == j
if (i != j)
{
// Converting Matrix to reduced row
// echelon form(diagonal matrix)
float p = a[j, i] / a[i, i];
for (k = 0; k <= n; k++)
a[j, k] = a[j, k] - (a[i, k]) * p;
}
}
}
return flag;
}
// Function to print the desired result
// if unique solutions exists, otherwise
// prints no solution or infinite solutions
// depending upon the input given.
static void PrintResult(float [,]a,
int n, int flag)
{
Console.Write("Result is : ");
if (flag == 2)
Console.WriteLine("Infinite Solutions Exists");
else if (flag == 3)
Console.WriteLine("No Solution Exists");
// Printing the solution by dividing
// constants by their respective
// diagonal elements
else
{
for (int i = 0; i < n; i++)
Console.Write(a[i, n] / a[i, i] + " ");
}
}
// To check whether infinite solutions
// exists or no solution exists
static int CheckConsistency(float [,]a,
int n, int flag)
{
int i, j;
float sum;
// flag == 2 for infinite solution
// flag == 3 for No solution
flag = 3;
for (i = 0; i < n; i++)
{
sum = 0;
for (j = 0; j < n; j++)
sum = sum + a[i, j];
if (sum == a[i, j])
flag = 2;
}
return flag;
}
// Driver code
public static void Main(String[] args)
{
float [,]a = {{ 0, 2, 1, 4 },
{ 1, 1, 2, 6 },
{ 2, 1, 1, 7 }};
// Order of Matrix(n)
int n = 3, flag = 0;
// Performing Matrix transformation
flag = PerformOperation(a, n);
if (flag == 1)
flag = CheckConsistency(a, n, flag);
// Printing Final Matrix
Console.WriteLine("Final Augmented Matrix is : ");
PrintMatrix(a, n);
Console.WriteLine("");
// Printing Solutions(if exist)
PrintResult(a, n, flag);
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// JavaScript Implementation for Gauss-Jordan
// Elimination Method
let M = 10;
// Function to print the matrix
function PrintMatrix(a,n)
{
for (let i = 0; i < n; i++)
{
for (let j = 0; j <= n; j++)
document.write(a[i][j] + " ");
document.write("<br>");
}
}
// function to reduce matrix to reduced
// row echelon form.
function PerformOperation(a,n)
{
let i, j, k = 0, c, flag = 0, m = 0;
let pro = 0;
// Performing elementary operations
for (i = 0; i < n; i++)
{
if (a[i][i] == 0)
{
c = 1;
while ((i + c) < n && a[i + c][i] == 0)
c++;
if ((i + c) == n)
{
flag = 1;
break;
}
for (j = i, k = 0; k <= n; k++)
{
let temp =a[j][k];
a[j][k] = a[j+c][k];
a[j+c][k] = temp;
}
}
for (j = 0; j < n; j++)
{
// Excluding all i == j
if (i != j)
{
// Converting Matrix to reduced row
// echelon form(diagonal matrix)
let p = a[j][i] / a[i][i];
for (k = 0; k <= n; k++)
a[j][k] = a[j][k] - (a[i][k]) * p;
}
}
}
return flag;
}
// Function to print the desired result
// if unique solutions exists, otherwise
// prints no solution or infinite solutions
// depending upon the input given.
function PrintResult(a,n,flag)
{
document.write("Result is : ");
if (flag == 2)
document.write("Infinite Solutions Exists<br>");
else if (flag == 3)
document.write("No Solution Exists<br>");
// Printing the solution by dividing constants by
// their respective diagonal elements
else {
for (let i = 0; i < n; i++)
document.write(a[i][n] / a[i][i] +" ");
}
}
// To check whether infinite solutions
// exists or no solution exists
function CheckConsistency(a,n,flag)
{
let i, j;
let sum;
// flag == 2 for infinite solution
// flag == 3 for No solution
flag = 3;
for (i = 0; i < n; i++)
{
sum = 0;
for (j = 0; j < n; j++)
sum = sum + a[i][j];
if (sum == a[i][j])
flag = 2;
}
return flag;
}
// Driver code
let a=[[ 0, 2, 1, 4 ],
[ 1, 1, 2, 6 ],
[ 2, 1, 1, 7 ]];
// Order of Matrix(n)
let n = 3, flag = 0;
// Performing Matrix transformation
flag = PerformOperation(a, n);
if (flag == 1)
flag = CheckConsistency(a, n, flag);
// Printing Final Matrix
document.write("Final Augmented Matrix is : <br>");
PrintMatrix(a, n);
document.write("<br>");
// Printing Solutions(if exist)
PrintResult(a, n, flag);
// This code is contributed by rag2127
</script>
Final Augmented Matrix is : 1 0 0 2.2 0 2 0 2.8 0 0 -2.5 -3 Result is : 2.2 1.4 1.2
Aplicaciones:
- Sistema de resolución de ecuaciones lineales: el método de eliminación de Gauss-Jordan se puede utilizar para encontrar la solución de un sistema de ecuaciones lineales que se aplica en las matemáticas.
- Determinación del determinante: la eliminación gaussiana se puede aplicar a una array cuadrada para encontrar el determinante de la array.
- Encontrar el inverso de la array: el método de eliminación de Gauss-Jordan se puede utilizar para determinar el inverso de una array cuadrada.
- Búsqueda de rangos y bases: utilizando la forma escalonada de fila reducida, los rangos y las bases de las arrays cuadradas se pueden calcular mediante el método de eliminación de Gauss.
Publicación traducida automáticamente
Artículo escrito por Ankit_Bisht y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA