Dada una función f(x) en el número flotante x y una suposición inicial para la raíz, encuentre la raíz de la función en el intervalo. Aquí f(x) representa una ecuación algebraica o trascendental.
Para simplificar, hemos supuesto que la derivada de la función también se proporciona como entrada.
Ejemplo:
Input: A function of x (for example x3 – x2 + 2),
derivative function of x (3x2 – 2x for above example)
and an initial guess x0 = -20
Output: The value of root is : -1.00
OR any other value close to root.
Hemos discutido a continuación los métodos para encontrar la raíz en el conjunto 1 y el conjunto 2
Conjunto 1: El método de bisección
Conjunto 2: El método de la posición falsa
Comparación con los dos métodos anteriores:
- En métodos anteriores, nos dieron un intervalo. Aquí se requiere un valor de estimación inicial de raíz.
- Se garantiza que los dos métodos anteriores convergen, Newton Raphson puede no converger en algunos casos.
- El método de Newton Raphson requiere derivada. Algunas funciones pueden ser difíciles o
imposibles de diferenciar. - Para muchos problemas, el método de Newton Raphson converge más rápido que los dos métodos anteriores.
- Además, puede identificar raíces repetidas, ya que no busca cambios en el signo de f(x) explícitamente
La fórmula:
a partir de la suposición inicial x 1 , el método de Newton Raphson utiliza la siguiente fórmula para encontrar el siguiente valor de x, es decir, x n+1 del valor anterior x n .
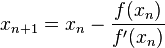
Ventajas del método de Newton Raphson:
- Es el mejor método para resolver las ecuaciones no lineales.
- También se puede utilizar para resolver el sistema de ecuaciones no lineales, diferenciales no lineales y ecuaciones integrales no lineales.
- El orden de convergencia es cuádrico, es decir, de segundo orden, lo que hace que este método sea más rápido en comparación con otros métodos.
- Es muy fácil de implementar en la computadora.
Desventajas del método de Newton Raphson:
- Este método se vuelve complicado si la derivada de la función f(x) no es simple.
- Este método requiere una gran y sensible atención en cuanto a la elección de su aproximación.
- En cada iteración, tenemos que evaluar dos cantidades f(x) y f'(x) para alguna x.
Algoritmo:
Entrada: x inicial, func(x), derivFunc(x)
Salida: Raíz de Func()
- Calcule los valores de func(x) y derivFunc(x) para una x inicial dada
- Calcule h: h = func(x) / derivFunc(x)
- Mientras que h es mayor que el error permitido ε
- h = func(x) / derivFunc(x)
- x = x – h
A continuación se muestra la implementación del algoritmo anterior.
C++
// C++ program for implementation of Newton Raphson Method for
// solving equations
#include<bits/stdc++.h>
#define EPSILON 0.001
using namespace std;
// An example function whose solution is determined using
// Bisection Method. The function is x^3 - x^2 + 2
double func(double x)
{
return x*x*x - x*x + 2;
}
// Derivative of the above function which is 3*x^x - 2*x
double derivFunc(double x)
{
return 3*x*x - 2*x;
}
// Function to find the root
void newtonRaphson(double x)
{
double h = func(x) / derivFunc(x);
while (abs(h) >= EPSILON)
{
h = func(x)/derivFunc(x);
// x(i+1) = x(i) - f(x) / f'(x)
x = x - h;
}
cout << "The value of the root is : " << x;
}
// Driver program to test above
int main()
{
double x0 = -20; // Initial values assumed
newtonRaphson(x0);
return 0;
}
Java
// Java program for implementation of
// Newton Raphson Method for solving
// equations
class GFG {
static final double EPSILON = 0.001;
// An example function whose solution
// is determined using Bisection Method.
// The function is x^3 - x^2 + 2
static double func(double x)
{
return x * x * x - x * x + 2;
}
// Derivative of the above function
// which is 3*x^x - 2*x
static double derivFunc(double x)
{
return 3 * x * x - 2 * x;
}
// Function to find the root
static void newtonRaphson(double x)
{
double h = func(x) / derivFunc(x);
while (Math.abs(h) >= EPSILON)
{
h = func(x) / derivFunc(x);
// x(i+1) = x(i) - f(x) / f'(x)
x = x - h;
}
System.out.print("The value of the"
+ " root is : "
+ Math.round(x * 100.0) / 100.0);
}
// Driver code
public static void main (String[] args)
{
// Initial values assumed
double x0 = -20;
newtonRaphson(x0);
}
}
// This code is contributed by Anant Agarwal.
Python3
# Python3 code for implementation of Newton
# Raphson Method for solving equations
# An example function whose solution
# is determined using Bisection Method.
# The function is x^3 - x^2 + 2
def func( x ):
return x * x * x - x * x + 2
# Derivative of the above function
# which is 3*x^x - 2*x
def derivFunc( x ):
return 3 * x * x - 2 * x
# Function to find the root
def newtonRaphson( x ):
h = func(x) / derivFunc(x)
while abs(h) >= 0.0001:
h = func(x)/derivFunc(x)
# x(i+1) = x(i) - f(x) / f'(x)
x = x - h
print("The value of the root is : ",
"%.4f"% x)
# Driver program to test above
x0 = -20 # Initial values assumed
newtonRaphson(x0)
# This code is contributed by "Sharad_Bhardwaj"
C#
// C# program for implementation of
// Newton Raphson Method for solving
// equations
using System;
class GFG {
static double EPSILON = 0.001;
// An example function whose solution
// is determined using Bisection Method.
// The function is x^3 - x^2 + 2
static double func(double x)
{
return x * x * x - x * x + 2;
}
// Derivative of the above function
// which is 3*x^x - 2*x
static double derivFunc(double x)
{
return 3 * x * x - 2 * x;
}
// Function to find the root
static void newtonRaphson(double x)
{
double h = func(x) / derivFunc(x);
while (Math.Abs(h) >= EPSILON)
{
h = func(x) / derivFunc(x);
// x(i+1) = x(i) - f(x) / f'(x)
x = x - h;
}
Console.Write("The value of the"
+ " root is : "
+ Math.Round(x * 100.0) / 100.0);
}
// Driver code
public static void Main ()
{
// Initial values assumed
double x0 = -20;
newtonRaphson(x0);
}
}
// This code is contributed by nitin mittal
PHP
<?php
// PHP program for implementation
// of Newton Raphson Method for
// solving equations
$EPSILON = 0.001;
// An example function whose
// solution is determined
// using Bisection Method.
// The function is x^3 - x^2 + 2
function func($x)
{
return $x * $x * $x -
$x * $x + 2;
}
// Derivative of the above
// function which is 3*x^x - 2*x
function derivFunc($x)
{
return 3 * $x *
$x - 2 * $x;
}
// Function to
// find the root
function newtonRaphson($x)
{
global $EPSILON;
$h = func($x) / derivFunc($x);
while (abs($h) >= $EPSILON)
{
$h = func($x) / derivFunc($x);
// x(i+1) = x(i) -
// f(x) / f'(x)
$x = $x - $h;
}
echo "The value of the ".
"root is : " , $x;
}
// Driver Code
$x0 = -20; // Initial values assumed
newtonRaphson($x0);
// This code is contributed by ajit
?>
Javascript
<script>
// JavaScript program for implementation of
// Newton Raphson Method for solving
// equations
let EPSILON = 0.001;
// An example function whose solution
// is determined using Bisection Method.
// The function is x^3 - x^2 + 2
function func(x)
{
return x * x * x - x * x + 2;
}
// Derivative of the above function
// which is 3*x^x - 2*x
function derivFunc(x)
{
return 3 * x * x - 2 * x;
}
// Function to find the root
function newtonRaphson(x)
{
let h = func(x) / derivFunc(x);
while (Math.abs(h) >= EPSILON)
{
h = func(x) / derivFunc(x);
// x(i+1) = x(i) - f(x) / f'(x)
x = x - h;
}
document.write("The value of the"
+ " root is : "
+ Math.round(x * 100.0) / 100.0);
}
// Driver program
// Initial values assumed
let x0 = -20;
newtonRaphson(x0);
// This code is contributed by susmitakundugoaldanga.
</script>
Producción:
The value of root is : -1.00
¿Como funciona esto?
La idea es dibujar una recta tangente a f(x) en el punto x 1 . El punto donde la línea tangente cruza el eje x debería ser una mejor estimación de la raíz que x 1 . Llame a este punto x 2 . Calcule f(x 2 ) y dibuje una recta tangente en x 2 .

Sabemos que la pendiente de la recta desde (x 1 , f(x 1 )) hasta (x 2 , 0) es f'(x 1 )) donde f’ representa la derivada de f.
f'(x1) = (0 - f(x1)) / (x2 - x1) f'(x1) * (x2 - x1) = - f(x1) x2 = x1 - f(x1) / f'(x1) By finding this point 'x2', we move closer towards the root. We have to keep on repeating the above step till we get really close to the root or we find it. In general, xn+1 = xn - f(xn) / f'(xn)
Explicación alternativa usando la serie de Taylor:
Let x1 be the initial guess. We can write x2 as below: xn+1 = xn + h ------- (1) Here h would be a small value that can be positive or negative. According to Taylor's Series, ƒ(x) that is infinitely differentiable can be written as below f(xn+1) = f(xn + h) = f(xn) + h*f'(xn) + ((h*h)/2!)*(f''(xn)) + ... Since we are looking for root of function, f(xn+1) = 0 f(xn) + h*f'(xn) + ((h*h)/2!)*(f''(xn)) + ... = 0 Now since h is small, h*h would be very small. So if we ignore higher order terms, we get f(xn) + h*f'(xn) = 0 Substituting this value of h = xn+1 - xn from equation (1) we get, f(xn) + (xn+1 - xn)*f'(xn) = 0 xn+1 = xn - f(xn) / f'(xn)
Notas:
- Generalmente usamos este método para mejorar el resultado obtenido por el método de bisección o el método de posición falsa.
- El método babilónico para la raíz cuadrada se deriva del método de Newton-Raphson.
Referencias:
Métodos introductorios de análisis numérico por SS Sastry
https://en.wikipedia.org/wiki/Newton’s_method
http://www.cae.tntech.edu/Members/renfro/me2000/lectures/2004-09-07_handouts .pdf/at_download/file
Este artículo es una contribución de Abhiraj Smit . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA