Programa para hallar coeficiente de correlación

Dados dos elementos de array, tenemos que encontrar el coeficiente de correlación entre dos arrays. El coeficiente de correlación es una ecuación que se utiliza para determinar la fuerza de la relación entre dos variables. El coeficiente de correlación a veces se denomina coeficiente de correlación cruzada. El coeficiente de correlación siempre se encuentra entre -1 y +1, donde -1 representa que X e Y están correlacionados negativamente y +1 representa que X e Y están correlacionados positivamente.

$r=\frac{n\left(\sum x y\right)-\left(\sum x\right)\left(\sum y\right)}{\sqrt{\left[n \sum x^{2}-\left(\sum x\right)^{2}\right]\left[n \Sigma y^{2}-\left(\sum y\right)^{2}\right]}}$

Donde r es el coeficiente de correlación.

$\begin{array}{|c|c|} \hline X & Y \\ \hline 15 & 25 \\ \hline 18 & 25 \\ \hline 21 & 27 \\ \hline 24 & 31 \\ \hline 27 & 32 \\ \hline \Sigma X=105 & \sum Y=140 \end{array}$
$\begin{array}{|c|c|c|} \hline X^{*} Y & X^{*} X & Y^{*} Y \\ \hline 375 & 225 & 625 \\ \hline 450 & 324 & 625 \\ \hline 567 & 441 & 729 \\ \hline 744 & 576 & 961 \\ \hline 864 & 729 & 1024 \\ \hline \sum X^{*} Y=3000 & \sum X^{*} X=2295 & \sum Y^{*} Y=3964 \\ \hline \end{array}$

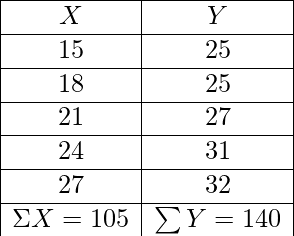
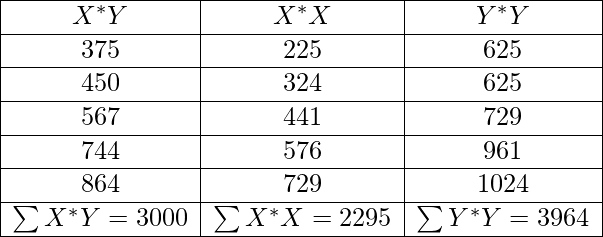
Correlation coefficient 
= (5 * 3000 - 105 * 140) 
     / sqrt((5 * 2295 - 105²)*(5*3964 - 140²))
= 300 / sqrt(450 * 220) = 0.953463

Ejemplos:

Input : X[] = {43, 21, 25, 42, 57, 59}
        Y[] = {99, 65, 79, 75, 87, 81}
Output : 0.529809

Input : X[] = {15, 18, 21, 24, 27};
        Y[] = {25, 25, 27, 31, 32}
Output : 0.953463

C++

// Program to find correlation coefficient
#include<bits/stdc++.h>
  
using namespace std;
  
// function that returns correlation coefficient.
float correlationCoefficient(int X[], int Y[], int n)
{
  
    int sum_X = 0, sum_Y = 0, sum_XY = 0;
    int squareSum_X = 0, squareSum_Y = 0;
  
    for (int i = 0; i < n; i++)
    {
        // sum of elements of array X.
        sum_X = sum_X + X[i];
  
        // sum of elements of array Y.
        sum_Y = sum_Y + Y[i];
  
        // sum of X[i] * Y[i].
        sum_XY = sum_XY + X[i] * Y[i];
  
        // sum of square of array elements.
        squareSum_X = squareSum_X + X[i] * X[i];
        squareSum_Y = squareSum_Y + Y[i] * Y[i];
    }
  
    // use formula for calculating correlation coefficient.
    float corr = (float)(n * sum_XY - sum_X * sum_Y) 
                  / sqrt((n * squareSum_X - sum_X * sum_X) 
                      * (n * squareSum_Y - sum_Y * sum_Y));
  
    return corr;
}
  
// Driver function
int main()
{
  
    int X[] = {15, 18, 21, 24, 27};
    int Y[] = {25, 25, 27, 31, 32};
  
    //Find the size of array.
    int n = sizeof(X)/sizeof(X[0]);
  
    //Function call to correlationCoefficient.
    cout<<correlationCoefficient(X, Y, n);
  
    return 0;
}

Java

// JAVA Program to find correlation coefficient
import java.math.*;
  
class GFG {
  
    // function that returns correlation coefficient.
    static float correlationCoefficient(int X[],
                                    int Y[], int n)
    {
       
        int sum_X = 0, sum_Y = 0, sum_XY = 0;
        int squareSum_X = 0, squareSum_Y = 0;
       
        for (int i = 0; i < n; i++)
        {
            // sum of elements of array X.
            sum_X = sum_X + X[i];
       
            // sum of elements of array Y.
            sum_Y = sum_Y + Y[i];
       
            // sum of X[i] * Y[i].
            sum_XY = sum_XY + X[i] * Y[i];
       
            // sum of square of array elements.
            squareSum_X = squareSum_X + X[i] * X[i];
            squareSum_Y = squareSum_Y + Y[i] * Y[i];
        }
       
        // use formula for calculating correlation 
        // coefficient.
        float corr = (float)(n * sum_XY - sum_X * sum_Y)/
                     (float)(Math.sqrt((n * squareSum_X -
                     sum_X * sum_X) * (n * squareSum_Y - 
                     sum_Y * sum_Y)));
       
        return corr;
    }
       
    // Driver function
    public static void main(String args[])
    {
       
        int X[] = {15, 18, 21, 24, 27};
        int Y[] = {25, 25, 27, 31, 32};
       
        // Find the size of array.
        int n = X.length;
       
        // Function call to correlationCoefficient.
        System.out.printf("%6f",
                 correlationCoefficient(X, Y, n));
       
          
    }
}
  
/*This code is contributed by Nikita Tiwari.*/

Python

# Python Program to find correlation coefficient.
import math
  
# function that returns correlation coefficient.
def correlationCoefficient(X, Y, n) :
    sum_X = 0
    sum_Y = 0
    sum_XY = 0
    squareSum_X = 0
    squareSum_Y = 0
      
      
    i = 0
    while i < n :
        # sum of elements of array X.
        sum_X = sum_X + X[i]
          
        # sum of elements of array Y.
        sum_Y = sum_Y + Y[i]
          
        # sum of X[i] * Y[i].
        sum_XY = sum_XY + X[i] * Y[i]
          
        # sum of square of array elements.
        squareSum_X = squareSum_X + X[i] * X[i]
        squareSum_Y = squareSum_Y + Y[i] * Y[i]
          
        i = i + 1
       
    # use formula for calculating correlation 
    # coefficient.
    corr = (float)(n * sum_XY - sum_X * sum_Y)/
           (float)(math.sqrt((n * squareSum_X - 
           sum_X * sum_X)* (n * squareSum_Y - 
           sum_Y * sum_Y)))
    return corr
      
# Driver function
X = [15, 18, 21, 24, 27]
Y = [25, 25, 27, 31, 32]
       
# Find the size of array.
n = len(X)
  
# Function call to correlationCoefficient.
print ('{0:.6f}'.format(correlationCoefficient(X, Y, n)))
  
# This code is contributed by Nikita Tiwari.

C#

// C# Program to find correlation coefficient
using System;
  
class GFG {
   
    // function that returns correlation coefficient.
    static float correlationCoefficient(int []X, int []Y,
                                                   int n)
    {
        int sum_X = 0, sum_Y = 0, sum_XY = 0;
        int squareSum_X = 0, squareSum_Y = 0;
        
        for (int i = 0; i < n; i++)
        {
            // sum of elements of array X.
            sum_X = sum_X + X[i];
        
            // sum of elements of array Y.
            sum_Y = sum_Y + Y[i];
        
            // sum of X[i] * Y[i].
            sum_XY = sum_XY + X[i] * Y[i];
        
            // sum of square of array elements.
            squareSum_X = squareSum_X + X[i] * X[i];
            squareSum_Y = squareSum_Y + Y[i] * Y[i];
        }
        
        // use formula for calculating correlation 
        // coefficient.
        float corr = (float)(n * sum_XY - sum_X * sum_Y)/
                     (float)(Math.Sqrt((n * squareSum_X -
                     sum_X * sum_X) * (n * squareSum_Y - 
                     sum_Y * sum_Y)));
        
        return corr;
    }
        
    // Driver function
    public static void Main()
    {
        
        int []X = {15, 18, 21, 24, 27};
        int []Y = {25, 25, 27, 31, 32};
        
        // Find the size of array.
        int n = X.Length;
        
        // Function call to correlationCoefficient.
        Console.Write(Math.Round(correlationCoefficient(X, Y, n) *
                                            1000000.0)/1000000.0);
        
           
    }
}
   
//This code is contributed by Anant Agarwal.

PHP

<?php
// PHP Program to find
// correlation coefficient
  
// function that returns 
// correlation coefficient.
function correlationCoefficient($X, $Y, $n)
{
    $sum_X = 0;$sum_Y = 0; $sum_XY = 0;
    $squareSum_X = 0; $squareSum_Y = 0;
  
    for ($i = 0; $i < $n; $i++)
    {
        // sum of elements of array X.
        $sum_X = $sum_X + $X[$i];
  
        // sum of elements of array Y.
        $sum_Y = $sum_Y + $Y[$i];
  
        // sum of X[i] * Y[i].
        $sum_XY = $sum_XY + $X[$i] * $Y[$i];
  
        // sum of square of array elements.
        $squareSum_X = $squareSum_X + 
                       $X[$i] * $X[$i];
        $squareSum_Y = $squareSum_Y + 
                       $Y[$i] * $Y[$i];
    }
  
    // use formula for calculating
    // correlation coefficient.
    $corr = (float)($n * $sum_XY - $sum_X * $sum_Y) / 
         sqrt(($n * $squareSum_X - $sum_X * $sum_X) * 
              ($n * $squareSum_Y - $sum_Y * $sum_Y));
  
    return $corr;
}
  
// Driver Code
$X = array (15, 18, 21, 24, 27);
$Y = array (25, 25, 27, 31, 32);
  
//Find the size of array.
$n = sizeof($X);
  
//Function call to 
// correlationCoefficient.
echo correlationCoefficient($X, $Y, $n);
  
// This code is contributed by aj_36
?>

Javascript

<script>
  
// Javascript program to find correlation coefficient
  
// Function that returns correlation coefficient.
function correlationCoefficient(X, Y, n)
{
      
    let sum_X = 0, sum_Y = 0, sum_XY = 0;
    let squareSum_X = 0, squareSum_Y = 0;
     
    for(let i = 0; i < n; i++)
    {
          
        // Sum of elements of array X.
        sum_X = sum_X + X[i];
     
        // Sum of elements of array Y.
        sum_Y = sum_Y + Y[i];
     
        // Sum of X[i] * Y[i].
        sum_XY = sum_XY + X[i] * Y[i];
     
        // Sum of square of array elements.
        squareSum_X = squareSum_X + X[i] * X[i];
        squareSum_Y = squareSum_Y + Y[i] * Y[i];
    }
     
    // Use formula for calculating correlation 
    // coefficient.
    let corr = (n * sum_XY - sum_X * sum_Y)/
               (Math.sqrt((n * squareSum_X -
                       sum_X * sum_X) * 
                          (n * squareSum_Y - 
                       sum_Y * sum_Y)));
     
    return corr;
}
  
// Driver code
let X = [ 15, 18, 21, 24, 27 ];
let Y = [ 25, 25, 27, 31, 32 ];
  
// Find the size of array.
let n = X.length;
  
// Function call to correlationCoefficient.
document.write(
         correlationCoefficient(X, Y, n));
           
// This code is contributed by susmitakundugoaldanga  
  
</script>

Producción :

0.953463

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python

C#

PHP

Javascript

Deja una respuesta Cancelar la respuesta