Programa para hallar el valor de sin(nΘ)

Posted on by Rudeus Greyrat

Dado el valor de sin(Θ) y una variable n<=15. La tarea es encontrar el valor de sin(nΘ) usando la propiedad de las funciones trigonométricas.
Ejemplos : 
 

Input: sin(Θ)=0.5, n=1
Output: 0.5

Input: sin(Θ)=0.5, n=10
Output: -0.866025

Enfoque: Este problema se puede resolver usando el teorema de De moivre y el teorema del binomio 

\begin{document} Using De-Moivre's theorem, we have- \begin{align*} \cos(n\theta)+\iota \sin(n\theta)&=(\cos \theta+\iota \sin \theta)^n\\ &=\cos^n \theta +\binom{n}{1} \cos^{n-1} \theta (\iota \sin \theta)+\binom{n}{2} \cos^{n-2} \theta (\iota \sin \theta)^2+\\ & \binom{n}{3} \cos^{n-3} \theta (\iota \sin \theta)^3+ \cdots \\ \end{align*} Equating the result to imaginary part to get the value of $\sin n\theta$ finally, we got-\\ $\sin (n \theta)=\binom{n}{1}\cos^{n-1}\theta \sin \theta-\binom{n}{3}\cos^{n-3}\theta \sin^3 \theta+\binom{n}{5}\cos^{n-5}\theta \sin^5 \theta- \cdots$\\ As we have value of $\sin \theta$, \\ we can find value of $\cos \theta $\\ $$\cos \theta=\sqrt{1-\sin^2 \theta}$$ \end{document}

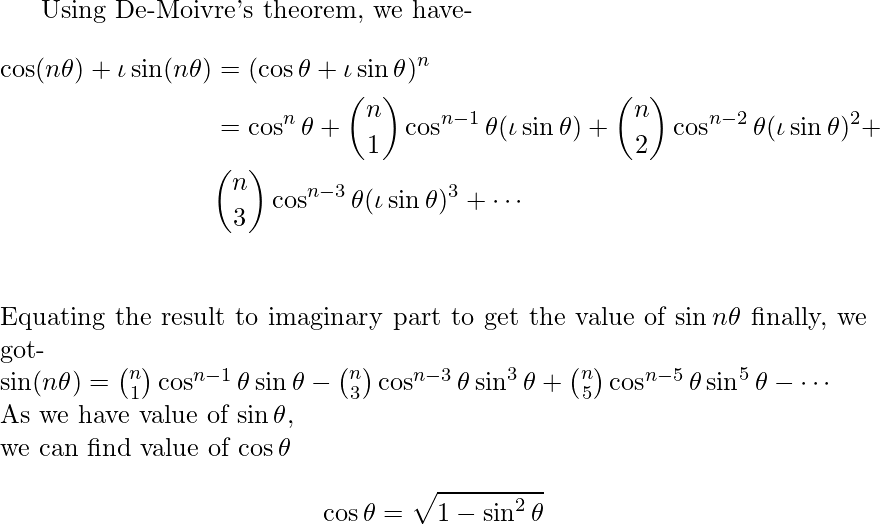
Ahora, tenemos tanto sen(Θ) como cos(Θ). Pon el valor en la ecuación para obtener tu respuesta.
A continuación se muestra la implementación del enfoque anterior: 
 

C++

// C++ Program to find the value of sin(n?)
#include <bits/stdc++.h>
#define ll long long int
#define MAX 16
using namespace std;
ll nCr[MAX][MAX] = { 0 };
  
// This function use to calculate the
// binomial coefficient upto 15
void binomial()
{
    // use simple DP to find coefficient
    for (int i = 0; i < MAX; i++) {
        for (int j = 0; j <= i; j++) {
            if (j == 0 || j == i)
                nCr[i][j] = 1;
            else
                nCr[i][j] = nCr[i - 1][j] + nCr[i - 1][j - 1];
        }
    }
}
  
// Function to find the value of
double findCosNTheta(double sinTheta, ll n)
{
    // find cosTheta from sinTheta
    double cosTheta = sqrt(1 - sinTheta * sinTheta);
  
    // store required answer
    double ans = 0;
    // use to toggle sign in sequence.
    ll toggle = 1;
    for (int i = 1; i <= n; i += 2) {
        ans = ans + nCr[n][i] * pow(cosTheta, n - i) 
                        * pow(sinTheta, i) * toggle;
        toggle = toggle * -1;
    }
    return ans;
}
  
// Driver code.
int main()
{
    binomial();
    double sinTheta = 0.5;
    ll n = 10;
  
    cout << findCosNTheta(sinTheta, n) << endl;
  
    return 0;
}

Java

// Java Program to find the value of sin(n?)
  
public class GFG {
      
    private static final int MAX = 16;
    static long nCr[][] = new long [MAX][MAX];
      
    // This function use to calculate the 
    // binomial coefficient upto 15 
    static void binomial() 
    { 
        // use simple DP to find coefficient 
        for (int i = 0; i < MAX; i++) { 
            for (int j = 0; j <= i; j++) { 
                if (j == 0 || j == i) 
                    nCr[i][j] = 1; 
                else
                    nCr[i][j] = nCr[i - 1][j] + nCr[i - 1][j - 1]; 
            } 
        } 
    } 
      
    // Function to find the value of 
    static double findCosNTheta(double sinTheta, int n) 
    { 
        // find cosTheta from sinTheta 
        double cosTheta = Math.sqrt(1 - sinTheta * sinTheta); 
      
        // store required answer 
        double ans = 0; 
        // use to toggle sign in sequence. 
        long toggle = 1; 
        for (int i = 1; i <= n; i += 2) { 
            ans = ans + nCr[n][i] * Math.pow(cosTheta, n - i) 
                            * Math.pow(sinTheta, i) * toggle; 
            toggle = toggle * -1; 
        } 
        return ans; 
    } 
      
  
      
    // Driver code 
    public static void main (String args[]){
            binomial(); 
            double sinTheta = 0.5; 
            int n = 10; 
              
            System.out.println(findCosNTheta(sinTheta, n));
    }
  
// This code is contributed by ANKITRAI1
}

Python3

# Python3 program to find the 
# value of sin(n-theta) 
  
import math 
MAX=16
nCr=[[0 for i in range(MAX)] for i in range(MAX)] 
  
# Function to calculate the binomial 
# coefficient upto 15 
def binomial(): 
      
    # use simple DP to find coefficient 
    for i in range(MAX): 
        for j in range(0,i+1): 
            if j == 0 or j == i: 
                nCr[i][j] = 1
            else: 
                nCr[i][j] = nCr[i - 1][j] + nCr[i - 1][j - 1] 
  
# Function to find the value of cos(n-theta) 
def findCosNTheta(sinTheta,n): 
      
    # find sinTheta from sinTheta 
    cosTheta = math.sqrt(1 - sinTheta * sinTheta) 
      
    # to store required answer 
    ans = 0
      
    # use to toggle sign in sequence. 
    toggle = 1
    for i in range(1,n+1,2): 
        ans = (ans + nCr[n][i]*(cosTheta**(n - i)) 
              *(sinTheta**i) * toggle) 
        toggle = toggle * -1
    return ans 
      
# Driver code 
if __name__=='__main__': 
    binomial() 
    sinTheta = 0.5
    n = 10
    print(findCosNTheta(sinTheta, n)) 
      
# this code is contributed by sahilshelangia 

C#

// C# Program to find the value of sin(n?)
using System;
  
class GFG 
{
  
private static int MAX = 16;
static long[,] nCr = new long [MAX, MAX];
  
// This function use to calculate the 
// binomial coefficient upto 15 
static void binomial() 
{ 
    // use simple DP to find coefficient 
    for (int i = 0; i < MAX; i++) 
    { 
        for (int j = 0; j <= i; j++) 
        { 
            if (j == 0 || j == i) 
                nCr[i, j] = 1; 
            else 
                nCr[i, j] = nCr[i - 1, j] + 
                            nCr[i - 1, j - 1]; 
        } 
    } 
} 
  
// Function to find the value of cos(n-theta) 
static double findCosNTheta(double sinTheta, int n) 
{ 
    // find cosTheta from sinTheta 
    double cosTheta = Math.Sqrt(1 - sinTheta * 
                                    sinTheta); 
  
    // store required answer 
    double ans = 0; 
      
    // use to toggle sign in sequence. 
    long toggle = 1; 
    for (int i = 1; i <= n; i += 2) 
    { 
        ans = ans + nCr[n, i] * Math.Pow(cosTheta, n - i) *
                                Math.Pow(sinTheta, i) * toggle; 
        toggle = toggle * -1; 
    } 
    return ans; 
} 
  
// Driver code 
public static void Main ()
{
    binomial(); 
    double sinTheta = 0.5; 
    int n = 10; 
      
    Console.Write(findCosNTheta(sinTheta, n));
}
}
  
// This code is contributed by ChitraNayal

PHP

<?php
// PHP Program to find the value of sin(n?)
$MAX=16;
$nCr=array_fill(0,$MAX,array_fill(0,$MAX,0));
  
// This function use to calculate the
// binomial coefficient upto 15
function binomial()
{
    global $MAX,$nCr;
    // use simple DP to find coefficient
    for ($i = 0; $i < $MAX; $i++) {
        for ($j = 0; $j <= $i; $j++) {
            if ($j == 0 || $j == $i)
                $nCr[$i][$j] = 1;
            else
                $nCr[$i][$j] = $nCr[$i - 1][$j] + $nCr[$i - 1][$j - 1];
        }
    }
}
  
// Function to find the value of
function findCosNTheta($sinTheta,$n)
{
    global $MAX,$nCr;
    // find cosTheta from sinTheta
    $cosTheta = sqrt(1 - $sinTheta * $sinTheta);
  
    // store required answer
    $ans = 0;
    // use to toggle sign in sequence.
    $toggle = 1;
    for ($i = 1; $i <= $n; $i += 2) {
        $ans = $ans + $nCr[$n][$i] * pow($cosTheta, $n - $i) 
                        * pow($sinTheta, $i) * $toggle;
        $toggle = $toggle * -1;
    }
    return $ans;
}
  
// Driver code.
  
    binomial();
    $sinTheta = 0.5;
    $n = 10;
  
    echo findCosNTheta($sinTheta, $n);
  
// this code is contributed by mits
?>

Javascript

<script>
  
// Javascript Program to find the value of sin(n?)
MAX = 16
var nCr = Array.from(Array(MAX), () => new Array(MAX));
  
// This function use to calculate the
// binomial coefficient upto 15
function binomial()
{
    // use simple DP to find coefficient
    for (var i = 0; i < MAX; i++) {
        for (var j = 0; j <= i; j++) {
            if (j == 0 || j == i)
                nCr[i][j] = 1;
            else
                nCr[i][j] = nCr[i - 1][j] + 
                nCr[i - 1][j - 1];
        }
    }
}
  
// Function to find the value of
function findCosNTheta(sinTheta, n)
{
    // find cosTheta from sinTheta
    var cosTheta = Math.sqrt(1 - sinTheta * sinTheta);
  
    // store required answer
    var ans = 0;
    // use to toggle sign in sequence.
    var toggle = 1;
    for (var i = 1; i <= n; i += 2) {
        ans = ans + nCr[n][i] * Math.pow(cosTheta, n - i)
                        * Math.pow(sinTheta, i) * toggle;
        toggle = toggle * -1;
    }
    return ans.toFixed(6);
}
  
// Driver code.
binomial();
var sinTheta = 0.5;
var n = 10;
document.write( findCosNTheta(sinTheta, n));
  
</script>
Producción: 

-0.866025

 

Publicación traducida automáticamente

Artículo escrito por sahilshelangia y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *