Programa para encontrar HCF iterativamente

HCF (máximo común divisor) o MCD (máximo común divisor) de dos números es el número más grande que divide a ambos. 
 

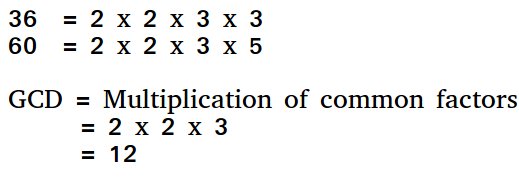
Por ejemplo, el MCD de 20 y 28 es 4 y el MCD de 98 y 56 es 14.
 

Hemos discutido la solución recursiva en la siguiente publicación. Programa recursivo para encontrar GCD o HCF de dos números
A continuación se muestra la implementación iterativa del algoritmo de Euclides 
 

// C++ program to find HCF of two
// numbers iteratively.
#include <bits/stdc++.h>
using namespace std;
 
int hcf(int a, int b)
{
    if (a == 0)
        return b;
    else if (b == 0)
        return a;
    while (a != b) {
        if (a > b)
            a = a - b;
        else
            b = b - a;
    }
    return a;
}
 
// Driver code
int main()
{
    int a = 60, b = 96;
    cout << hcf(a, b) << endl;
    return 0;
}
 
// This code is contributed by shubhamsingh10

// C program to find HCF of two
// numbers iteratively.
#include <stdio.h>
 
int hcf(int a, int b)
{
    if (a == 0)
        return b;
    else if (b == 0)
        return a;
    while (a != b) {
        if (a > b)
            a = a - b;
        else
            b = b - a;
    }
    return a;
}
int main()
{
    int a = 60, b = 96;
    printf("%d\n", hcf(a, b));
    return 0;
}

// JAVA Code for Program to find
// HCF iteratively
import java.util.*;
 
class GFG {
 
    static int hcf(int a, int b)
    {
        if (a == 0)
            return b;
        else if (b == 0)
            return a;
        while (a != b) {
            if (a > b)
                a = a - b;
            else
                b = b - a;
        }
        return a;
    }
 
    /* Driver program */
    public static void main(String[] args)
    {
        int a = 60, b = 96;
        System.out.println(hcf(a, b));
    }
}
 
// This code is contributed by Arnav Kr. Mandal.

// Python program to find HCF of two
// numbers iteratively.
 
 
def hcf(a, b):
    if(a == 0):
      return b
    else if(b == 0):
      return a
    while (a != b):
        if (a > b):
            a = a - b
        else:
            b = b - a
    return a
 
 
a = 60
b = 96
print(hcf(a, b))

// C# Code for Program to find
// HCF iteratively
using System;
 
class GFG {
 
    static int hcf(int a, int b)
    {
        if (a == 0)
            return b;
        else if (b == 0)
            return a;
        while (a != b) {
            if (a > b)
                a = a - b;
            else
                b = b - a;
        }
        return a;
    }
 
    // Driver program
    public static void Main()
    {
        int a = 60, b = 96;
        Console.WriteLine(hcf(a, b));
    }
}
 
// This code is contributed by vt_m.

<?php
//PHP program to find HCF of two
// numbers iteratively.
 
function hcf($a, $b)
{   if($a==0)
      return $b;
   else if($b==0)
      return $a;
    while ($a != $b) {
        if ($a > $b)    
            $a = $a - $b;    
        else
            $b = $b - $a;    
    }
     
    return $a;
}
 
// Driver code
$a = 60; $b = 96;
echo hcf($a, $b), "\n";
     
// This code is contributed by ajit
?>

<script>
 
//Javascript program to find HCF of two
// numbers iteratively.
 
function hcf(a, b)
{   if (a == 0)
        return b;
    else if (b == 0)
        return a;
    while (a != b)
    {
        if (a > b)    
            a = a - b;    
        else   
            b = b - a;    
    }
    return a;
}
 
// Driver code
    let a = 60, b = 96;
    document.write(hcf(a, b) + "<br>");    
 
// This code is contributed by Mayank Tyagi
 
</script>

Producción: 

12

Complejidad del tiempo: O(max(a, b))

Espacio Auxiliar: O(1)