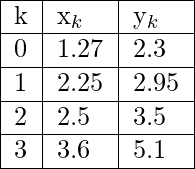
La tarea dada es encontrar el valor de x para un y dado de una función desconocida y = f(x) donde se dan los valores de algunos pares de puntos (x, y).
Sea y = f(x) una función desconocida donde x es una variable independiente.
Para diferentes valores de x, digamos ![]() [Tex]x_k, k=0, 1, 2, 3…m) [/Tex]valores de los respectivos
[Tex]x_k, k=0, 1, 2, 3…m) [/Tex]valores de los respectivos ![]() [Tex]y_k = f(x_k), k=0, 1, 2, 3 …m) [/Tex]dado.
[Tex]y_k = f(x_k), k=0, 1, 2, 3 …m) [/Tex]dado.
El proceso de encontrar el valor de la variable independiente x para un valor dado de y que se encuentra entre dos valores tabulados con la ayuda del conjunto dado de observación para una función desconocida se conoce como interpolación inversa .
Esto se usa a menudo para verificar si la salida y para una función desconocida es correcta, es decir, cuánto difiere el argumento x para esta salida y de la entrada original.
El problema de la interpolación inversa se puede resolver utilizando la fórmula de Lagrange .
Fórmula de Lagrange:
La fórmula para la interpolación inversa es similar a la fórmula de interpolación pero con pocos cambios.
Aquí, para resolver el problema de la interpolación inversa, se intercambian los lugares de x e y. La fórmula para la interpolación inversa es: 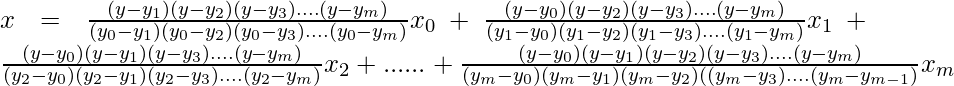
Este método se puede usar incluso cuando los puntos están espaciados de manera desigual. Aquí x se expresa como una función de y.
Ejemplos:
Entrada: Encuentra el valor de x donde y = 4.5 y los puntos dados son:
Salida: 2.79501
Explicación: Aquí el número de puntos de datos dados = 4 y y = 4.5
Entonces, poniendo los valores de todos los x e y en la fórmula de interpolación inversa dada arriba obtenemos,
De aquí obtenemos,
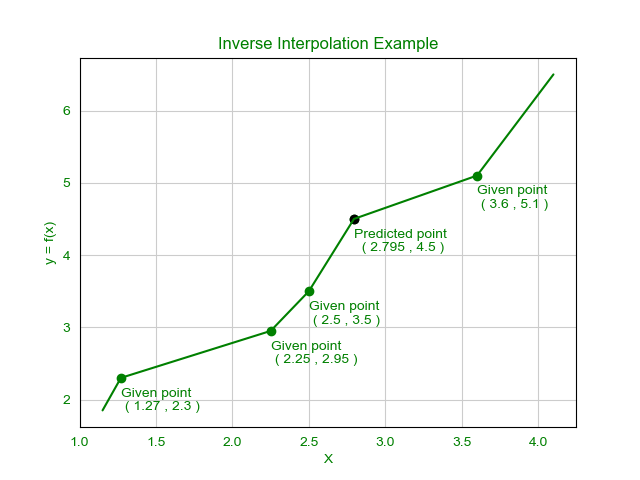
El valor de x = 2.79501 donde el valor de y = 4.5
Grafico:
Algoritmo:
aquí, los datos son una lista de puntos que consisten en x e y, y n es el número de puntos de datos.
PASO – 1 : Inicializar el valor final x = 0
PASO – 2 : PARA i = 1 a n hacer
PASO – 3 : Inicializar xi = data[i].x
PASO – 4 : PARA j = 1 a n hacer
PASO – 5 : IF i != j do
STEP – 6 : Multiplique xi por ( y – data[j].y ) y divida por ( data[i].y – data[j].y )
ENDIF
ENDFOR
STEP – 7 : Sume xi a x
ENDFOR
STEP – 8 : Devuelve el valor final de x
STEP – 9 : FIN
Implementación:
C++
// C++ code for solving inverse interpolation
#include <bits/stdc++.h>
using namespace std;
// Consider a structure
// to keep each pair of
// x and y together
struct Data {
double x, y;
};
// Function to calculate
// the inverse interpolation
double inv_interpolate(Data d[], int n, double y)
{
// Initialize final x
double x = 0;
int i, j;
for (i = 0; i < n; i++) {
// Calculate each term
// of the given formula
double xi = d[i].x;
for (j = 0; j < n; j++) {
if (j != i) {
xi = xi
* (y - d[j].y)
/ (d[i].y - d[j].y);
}
}
// Add term to final result
x += xi;
}
return x;
}
// Driver Code
int main()
{
// Sample dataset of 4 points
// Here we find the value
// of x when y = 4.5
Data d[] = { { 1.27, 2.3 },
{ 2.25, 2.95 },
{ 2.5, 3.5 },
{ 3.6, 5.1 } };
// Size of dataset
int n = 4;
// Sample y value
double y = 4.5;
// Using the Inverse Interpolation
// function to find the
// value of x when y = 4.5
cout << "Value of x at y = 4.5 : "
<< inv_interpolate(d, n, y);
return 0;
}
Java
// Java code for solving inverse interpolation
class GFG
{
// Consider a structure
// to keep each pair of
// x and y together
static class Data
{
double x, y;
public Data(double x, double y)
{
super();
this.x = x;
this.y = y;
}
};
// Function to calculate
// the inverse interpolation
static double inv_interpolate(Data []d, int n, double y)
{
// Initialize final x
double x = 0;
int i, j;
for (i = 0; i < n; i++)
{
// Calculate each term
// of the given formula
double xi = d[i].x;
for (j = 0; j < n; j++)
{
if (j != i)
{
xi = xi
* (y - d[j].y)
/ (d[i].y - d[j].y);
}
}
// Add term to final result
x += xi;
}
return x;
}
// Driver Code
public static void main(String[] args)
{
// Sample dataset of 4 points
// Here we find the value
// of x when y = 4.5
Data []d = { new Data( 1.27, 2.3 ),
new Data( 2.25, 2.95 ),
new Data( 2.5, 3.5 ),
new Data( 3.6, 5.1 ) };
// Size of dataset
int n = 4;
// Sample y value
double y = 4.5;
// Using the Inverse Interpolation
// function to find the
// value of x when y = 4.5
System.out.printf("Value of x at y = 4.5 : %.5f"
, inv_interpolate(d, n, y));
}
}
// This code is contributed by Rajput-Ji
Python3
# Python3 code for solving
# inverse interpolation
# Consider a structure
# to keep each pair of
# x and y together
class Data:
def __init__(self, x, y):
self.x = x
self.y = y
# Function to calculate
# the inverse interpolation
def inv_interpolate(d: list, n: int,
y: float) -> float:
# Initialize final x
x = 0
for i in range(n):
# Calculate each term
# of the given formula
xi = d[i].x
for j in range(n):
if j != i:
xi = (xi * (y - d[j].y) /
(d[i].y - d[j].y))
# Add term to final result
x += xi
return x
# Driver Code
if __name__ == "__main__":
# Sample dataset of 4 points
# Here we find the value
# of x when y = 4.5
d = [Data(1.27, 2.3),
Data(2.25, 2.95),
Data(2.5, 3.5),
Data(3.6, 5.1)]
# Size of dataset
n = 4
# Sample y value
y = 4.5
# Using the Inverse Interpolation
# function to find the
# value of x when y = 4.5
print("Value of x at y = 4.5 :",
round(inv_interpolate(d, n, y), 5))
# This code is contributed by
# sanjeev2552
C#
// C# code for solving inverse interpolation
using System;
class GFG
{
// Consider a structure to keep
// each pair of x and y together
class Data
{
public double x, y;
public Data(double x, double y)
{
this.x = x;
this.y = y;
}
};
// Function to calculate the
// inverse interpolation
static double inv_interpolate(Data []d,
int n, double y)
{
// Initialize readonly x
double x = 0;
int i, j;
for (i = 0; i < n; i++)
{
// Calculate each term
// of the given formula
double xi = d[i].x;
for (j = 0; j < n; j++)
{
if (j != i)
{
xi = xi * (y - d[j].y) /
(d[i].y - d[j].y);
}
}
// Add term to readonly result
x += xi;
}
return x;
}
// Driver Code
public static void Main(String[] args)
{
// Sample dataset of 4 points
// Here we find the value
// of x when y = 4.5
Data []d = {new Data(1.27, 2.3),
new Data(2.25, 2.95),
new Data(2.5, 3.5),
new Data(3.6, 5.1)};
// Size of dataset
int n = 4;
// Sample y value
double y = 4.5;
// Using the Inverse Interpolation
// function to find the
// value of x when y = 4.5
Console.Write("Value of x at y = 4.5 : {0:f5}",
inv_interpolate(d, n, y));
}
}
// This code is contributed by Rajput-Ji
Javascript
<script>
// javascript code for solving inverse interpolation
// Consider a structure
// to keep each pair of
// x and y together
class Data {
constructor(x , y) {
this.x = x;
this.y = y;
}
};
// Function to calculate
// the inverse interpolation
function inv_interpolate( d , n , y)
{
// Initialize final x
var x = 0;
var i, j;
for (i = 0; i < n; i++) {
// Calculate each term
// of the given formula
var xi = d[i].x;
for (j = 0; j < n; j++) {
if (j != i) {
xi = xi * (y - d[j].y) / (d[i].y - d[j].y);
}
}
// Add term to final result
x += xi;
}
return x;
}
// Driver Code
// Sample dataset of 4 points
// Here we find the value
// of x when y = 4.5
var d = [ new Data(1.27, 2.3), new Data(2.25, 2.95), new Data(2.5, 3.5), new Data(3.6, 5.1) ];
// Size of dataset
var n = 4;
// Sample y value
var y = 4.5;
// Using the Inverse Interpolation
// function to find the
// value of x when y = 4.5
document.write("Value of x at y = 4.5 : ", inv_interpolate(d, n, y).toFixed(5));
// This code is contributed by gauravrajput1
</script>
Value of x at y = 4.5 : 2.79501
Complejidad: La complejidad temporal de la solución dada es O(n^2) y la complejidad espacial es O(1)
Publicación traducida automáticamente
Artículo escrito por Arghyadip_Manna y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA