Programa para la suma de series cosh(x) hasta el término N

Dados dos números x y N , la tarea es encontrar el valor de cosh(x) de la serie hasta N términos.
La expansión de cosh(x) se da a continuación: 
 

cosh(x) = 1 + x ² /2! + x ⁴ /4! + …………

Ejemplos: 
 

Input: x = 1, N = 5
Output: 1.54308035714

Input: x = 1, N = 10
Output: 1.54308063497

Enfoque: 
la serie anterior se puede implementar fácilmente usando una función factorial y bucles.
El enésimo término de la serie es: 
 

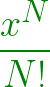
A continuación se muestra la implementación del enfoque anterior: 
 

// C++ program for
// the sum of cosh(x) series
 
#include <bits/stdc++.h>
using namespace std;
 
// function to return the factorial of a number
int fact(int n)
{
 
    int i = 1, fac = 1;
    for (i = 1; i <= n; i++)
        fac = fac * i;
 
    return fac;
}
 
// function to return the sum of the series
double log_Expansion(double x, int n)
{
 
    double sum = 0;
    int i = 0;
 
    for (i = 0; i < n; i++) {
 
        sum = sum
              + pow(x, 2 * i)
                    / fact(2 * i);
    }
 
    return sum;
}
 
// Driver code
int main()
{
    double x = 1;
    int n = 10;
    cout << setprecision(12)
         << log_Expansion(x, n)
         << endl;
 
    return 0;
}

// Java program for the sum of
// cosh(x) series
import java.util.*;
 
class GFG
{
 
// function to return the factorial of a number
static int fact(int n)
{
    int i = 1, fac = 1;
    for (i = 1; i <= n; i++)
        fac = fac * i;
 
    return fac;
}
 
// function to return the sum of the series
static double log_Expansion(double x, int n)
{
    double sum = 0;
    int i = 0;
 
    for (i = 0; i < n; i++)
    {
        sum = sum + Math.pow(x, 2 * i) /
                           fact(2 * i);
    }
 
    return sum;
}
 
// Driver code
public static void main(String[] args)
{
    double x = 1;
    int n = 10;
    System.out.println(log_Expansion(x, n));
}
}
 
// This code is contributed by 29AjayKumar

# Python3 program for the Sum of cosh(x) series
 
# function to return the factorial of a number
def fact(n):
 
    i, fac = 1, 1
    for i in range(1, n + 1):
        fac = fac * i
 
    return fac
 
# function to return the Sum of the series
def log_Expansion(x, n):
 
    Sum = 0
    i = 0
 
    for i in range(n):
 
        Sum = Sum + pow(x, 2 * i) / fact(2 * i)
 
    return Sum
 
# Driver code
x = 1
n = 10
print(log_Expansion(x, n))
 
# This code is contributed by Mohit Kumar

// C# program for the sum of
// cosh(x) series
using System;
 
class GFG
{
 
// function to return the
// factorial of a number
static int fact(int n)
{
    int i = 1, fac = 1;
    for (i = 1; i <= n; i++)
        fac = fac * i;
 
    return fac;
}
 
// function to return the sum of the series
static double log_Expansion(double x, int n)
{
    double sum = 0;
    int i = 0;
 
    for (i = 0; i < n; i++)
    {
        sum = sum + Math.Pow(x, 2 * i) /
                        fact(2 * i);
    }
 
    return sum;
}
 
// Driver code
public static void Main(String[] args)
{
    double x = 1;
    int n = 10;
    Console.WriteLine(log_Expansion(x, n));
}
}
 
// This code is contributed by PrinciRaj1992

<script>
 
// Javascript program for the sum of
// cosh(x) series
 
    // function to return the factorial of a number
    function fact( n) {
        let i = 1, fac = 1;
        for (i = 1; i <= n; i++)
            fac = fac * i;
 
        return fac;
    }
 
    // function to return the sum of the series
    function log_Expansion( x , n) {
        let sum = 0;
        let i = 0;
 
        for (i = 0; i < n; i++) {
            sum = sum + Math.pow(x, 2 * i) / fact(2*i);
        }
 
        return sum;
    }
 
    // Driver code
      
        let x = 1;
        let n = 10;
        document.write(log_Expansion(x, n).toFixed(11));
 
// This code is contributed by shikhasingrajput
 
</script>

1.54308063497

Complejidad de tiempo: O(n ² ), donde n representa el valor del entero dado.
Espacio auxiliar: O(1), no se requiere espacio adicional, por lo que es una constante.