Programación lineal

Todos nos encontramos con muchas situaciones basadas en objetivos en la vida cotidiana. ¿Se te ocurre alguna? Digamos que un estudiante tiene que completar un proyecto en 15 días o un vendedor tiene que lograr un objetivo de ventas en un mes, mientras que otra persona tiene que comprar un aparato electrónico con un presupuesto de 500 rupias, analice estas situaciones e intente encontrar la principal objetivo a alcanzar por cada persona individualmente. Digamos cuál es el objetivo de la estudiante en este caso, sí, ella quiere lograr la máxima puntuación en este proyecto, ¿puede decirme el objetivo del vendedor en este caso? Sí, su objetivo sería lograr las máximas ventas posibles en un mes. ¿Cuál crees que sería el objetivo de una persona que compra un dispositivo? Intentaría minimizar el costo tanto como sea posible. 

En matemáticas, un problema de Optimización puede implicar encontrar la máxima ganancia, el mínimo costo o tal vez el mínimo uso de recursos. Puede haber muchos más ejemplos en nuestra vida cotidiana que deben resolverse utilizando las técnicas de Optimización, los problemas pueden ser tan simples como mencionado anteriormente, pero podría complicarse según la situación, ya hemos discutido el objetivo de las tres situaciones dadas, ahora podemos ver los factores importantes, identificaremos el factor limitante en cada caso. ¿que significa? pues en cada caso hay escasez de algunos recursos como es el primer caso, el tiempo límite para completar el proyecto es limitado el tiempo que se asignará para completar el proyecto está limitado a 15 días solo así mismo en el caso dos el tiempo en el factor limitante que la persona tiene para vender el máximo producto posible en un período de un mes lo que puede Usted dice sobre la tercera situación cuál es el factor limitante en este caso, la persona tiene que comprar el dispositivo dentro de un presupuesto predeterminado, es decir, la cantidad para gastar su dinero es el factor limitante, en este caso, este factor limitante, que es la escasez de recursos, actúa como una restricción. en encontrar las mejores soluciones de los problemas dados, pero ¿cómo se resuelven estos problemas de optimización en matemáticas? Son todas diferentes técnicas de resolución de problemas para resolver tales problemas, la técnica principal que discutiremos es la programación lineal.

¿Qué es la Programación Lineal? 

La programación lineal es una técnica que nos ayuda a encontrar la solución óptima para un problema dado, una solución óptima es aquella solución que es el mejor resultado posible de un problema particular dado. En términos simples, es el método para descubrir cómo hacer algo de la mejor manera posible con recursos limitados dados que necesita para hacer la utilización óptima de los recursos para lograr el mejor resultado posible en un objetivo particular. tales como el menor costo, el mayor margen o el menor tiempo en esos recursos tienen usos alternativos La situación que requiere una búsqueda de los mejores valores de las variables sujetas a ciertas restricciones son análisis de programación modificables. Estas situaciones no pueden ser manejadas por las herramientas usuales de Cálculo o análisis marginal. La técnica del cálculo solo puede manejar restricciones exactamente iguales, mientras que esta limitación no existe en el caso de problemas de programación lineal. Un problema de programación lineal tiene dos partes básicas:

• Primera Parte: Es la función objetivo que describe el propósito principal de la formación para maximizar algún retorno o minimizar algún.
• Segunda Parte: Es un conjunto constante, Es el sistema de igualdades o desigualdades que describen la condición o restricciones de la restricción bajo la cual se va a lograr la Optimización.

Tipos de problemas de programación lineal

Básicamente, hay muchos problemas diferentes de programación lineal, pero en este artículo nos ocuparemos de tres problemas principales de programación lineal.

1. Problemas de fabricación: los problemas de fabricación son el problema que trata con la cantidad de unidades que se deben producir o vender para maximizar las ganancias cuando cada producto requiere mano de obra fija, horas de máquina y materias primas.
2. Problemas de la dieta: se utiliza para calcular la cantidad de diferentes tipos de constituyentes que se incluirán en la dieta para minimizar el costo y sujeto a la disponibilidad de alimentos y sus precios.
3. Problemas de transporte: se utiliza para determinar el programa de transporte para encontrar la forma más económica de transportar un producto desde plantas/fábricas ubicadas en diferentes lugares a diferentes mercados.

Términos relacionados con problemas de programación lineal

Para resolver problemas de programación lineal, debe tener claro su concepto sobre las terminologías básicas utilizadas para resolver los primeros problemas de programación lineal que se detallan a continuación:

• Variable de decisión: las variables que compiten entre sí para compartir recursos limitados, como productos, servicios, etc. Están interrelacionadas y tienen una relación lineal que es capaz de decidir cuál es la mejor solución óptima, se denominan variables de decisión.
• Función objetivo : el problema debe haber sido un objetivo claro y bien definido que se pueda establecer cuantitativamente, como la maximización de la ganancia o la minimización del costo, etc. Todos estos ejemplos se incluyen en la categoría de la función objetivo.
• Restricciones: Son las restricciones impuestas a los recursos disponibles, como un número restringido de máquinas, material de trabajo, etc.
• Restricción Redundante: Algunas restricciones están visiblemente presentes pero no obstaculizan el proceso del problema en estudio se denomina restricción redundante.
• Solución Factible: Son el conjunto de todas las posibles soluciones en forma de variables que satisfacen las constantes.
• Solución Óptima: Es la mejor solución entre todas las posibles que apoya de la mejor manera el objetivo del problema.

Ejemplo de pregunta de LPP

Pregunta 1: Una empresa fabrica y vende dos tipos de productos y el costo de producción de cada unidad a y b es de 200 y 150 rupias respectivamente cada unidad de IELTS una ganancia de 20 rupias y cada unidad de mayor ganancia de 15 la empresa vendedora estima la demanda mensual de A y B a b como máximo de la unidad cosechada en total el presupuesto de producción para el mes se fija en rupias 50000 cuántas unidades debe fabricar la empresa para obtener la máxima ganancia en sus ventas mensuales de a y b?

Solución:

Sea x = número de unidades de tipo A

y = Número de unidades de tipo B

Maximizar Z = 40x + 50y

Sujeto a las restricciones

3x + y ≤ 9

x + 2y ≤ 8

y x, y ≥ 0

Considere la ecuación,

3x + y = 9

x = 3

y = 0

y x + 2y = 8

x = 8

y = 0

Ahora, podemos determinar el valor máximo de Z evaluando el valor de Z en los cuatro puntos (vértices) que se muestran a continuación

vértices	Z = 40x + 50y
(0, 0)	Z = 40 × 0 + 50 × 0 = Rs. 0
(3, 0)	Z = 40 × 3 + 50 × 0 = Rs. 120
(0, 4)	Z = 40 × 0 + 50 × 4 = Rs. 200
(2, 3)	Z = 40 × 2 + 50 × 3 = Rs. 230

           

Beneficio máximo, Z = Rs. 230

∴ El número de unidades del tipo A es 2 y el número de unidades del tipo B es 3.

Pregunta 2: Maximizar Z = 3x + 4y 

Sujeto a restricciones, x + y ≤ 450, 2x + y ≤ 600 y x, y ≤ 0.

Solución: 

Tenemos de lo dado

Restricciones (1)

X + Y = 450

Haciendo x = 0, ⇒ 0 + y = 450 ⇒ y = 450

Haciendo y = 0, ⇒ x + 0 = 450 ⇒ x = 450

Desde, Restricciones (2)

2x + y = 600

Haciendo x = 0, ⇒ 0 + y = 600 ⇒ y = 600

Haciendo y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300

Ahora tenemos los puntos coordenados Z = 3x + 4y

vértices	Z = 3x + 4y
(0, 0)	Z = 3 × 0 + 4 × 0 = 0
(300, 0)	Z = 3 × 300+ 4 × 0 = 900
(150, 300)	Z = 3 × 150 + 4 × 300 = 1650
(0, 450)	Z = 3 × 0 + 4 × 450 = 1800

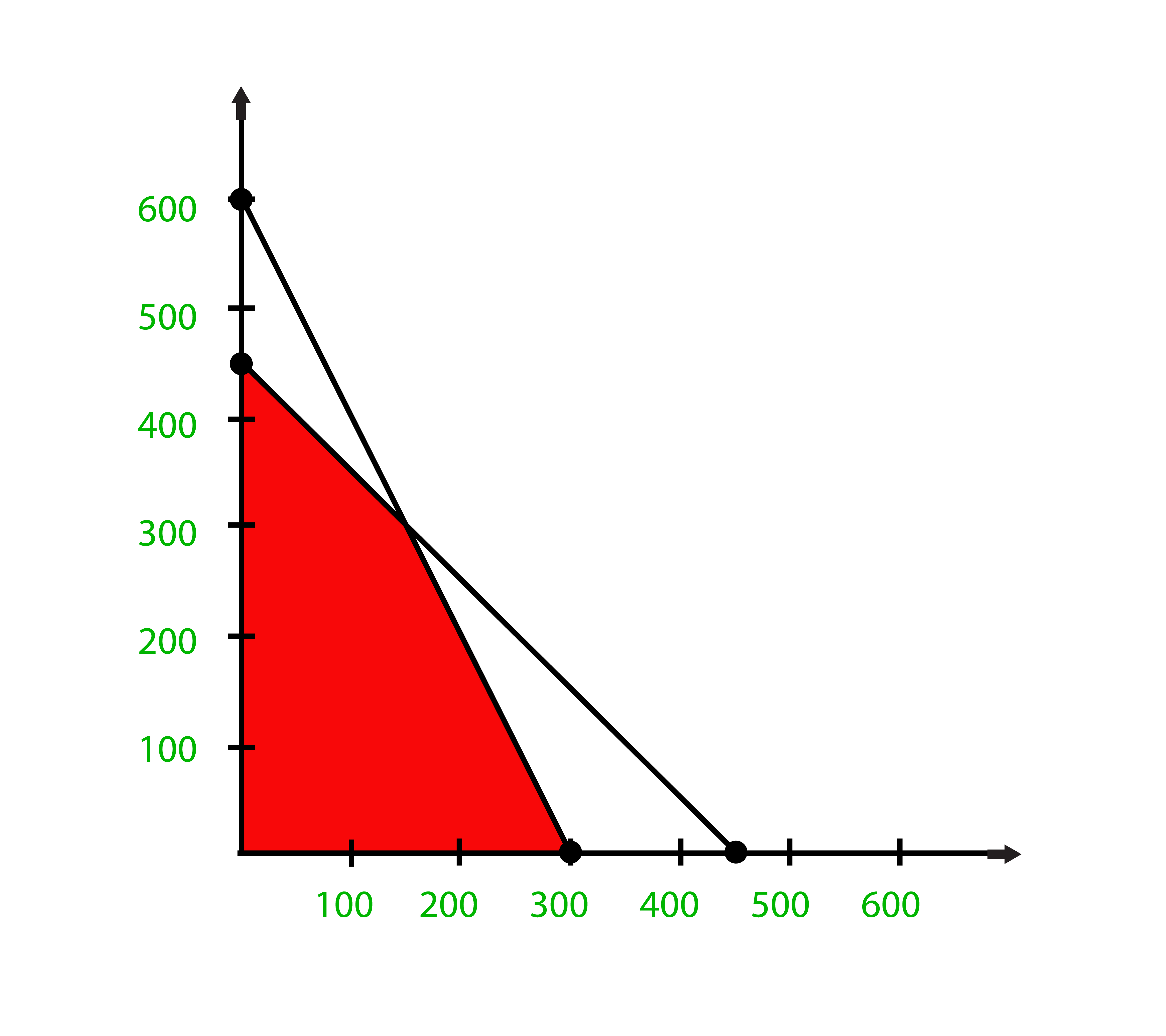
Por lo tanto, la solución óptima máxima Z = 1800 en la coordenada x = 0 y y = 450. El gráfico se muestra a continuación.