Una integral que tiene un límite se conoce como integral definida. Tiene un límite superior y un límite inferior. se representa como
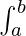 f(x) = F(b) − F(a)
f(x) = F(b) − F(a)
Hay muchas propiedades con respecto a la integral definida. Discutiremos cada propiedad una por una con pruebas también.
Propiedades
Propiedad 1: 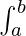 f(x) dx =
f(x) dx = 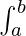 f(y) dy
f(y) dy
Prueba:
f(x) dx…….(1)
Supongamos que x = y
dx = dy
Poniendo esto en la ecuación (1)
f(y) día
Propiedad 2: 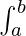 f(x) dx = –
f(x) dx = – 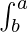 f(x) dx
f(x) dx
Prueba:
f(x) dx = F(b) – F(a)……..(1)
f(x) dx = F(a) – F(b)………. (2)
De (1) y (2)
Podemos derivar
f(x) dx = –
f(x) dx
Propiedad 3: 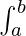 f(x) dx =
f(x) dx =  f(x) dx +
f(x) dx + 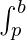 f(x) dx
f(x) dx
Prueba:
f(x) dx = F(b) – F(a) ………..(1)
f(x) dx = F(p) – F(a) ………..(2)
f(x) dx = F(b) – F(p) ………..(3)
De (2) y (3)
f(x) dx +
f(x) dx = F(p) – F(a) + F(b) – F(p)
f(x) dx +
f(x) dx = F(b) – F(a) =
f(x) dx
Por lo tanto, está probado.
Propiedad 4.1: 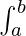 f(x) dx =
f(x) dx = 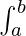 f(a + b – x) dx
f(a + b – x) dx
Prueba:
Suponer
a + b – x = y…………(1)
-dx = dy
Desde (1) puedes ver
cuando x = un
y = a + b – a
y = segundo
y cuando x = b
y = a + b – b
y = un
Reemplazando por estos valores, la integración en el lado derecho se convierte en
f(y)dy
De la propiedad 1 y la propiedad 2 se puede decir que
f(x) dx =
f(a + b – x) dx
Propiedad 4.2: Si el valor de a se da como 0, entonces la propiedad 4.1 se puede escribir como
f(x) dx =
f(b – x) dx
Propiedad 5: 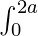 f(x) dx =
f(x) dx =  f(x) dx +
f(x) dx +  f(2a – x) dx
f(2a – x) dx
Prueba:
Podemos escribir
f(x) dx como
f(x) dx =
f(x) dx +
f(x) dx ………….. (1)
yo = yo 1 + yo 2
(de la propiedad 3)
Supongamos que 2a – x = y
-dx = dy
También cuando x = 0
y = 2a, y cuando x = a
y = 2a – a = a
Entonces,
f(2a – x)dx se puede escribir como
f(y) dy = yo 2
Reemplazando la ecuación (1) con el valor de I 2 obtenemos
f(x) dx =
f(x) dx +
f(2a – x) dx
Propiedad 6: 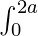 f(x) dx = 2
f(x) dx = 2  f(x) dx; si f(2a – x) = f(x)
f(x) dx; si f(2a – x) = f(x)
= 0 ; si f(2a – x) = -f(x)
Prueba:
De la propiedad 5 podemos escribir
f(x) dx como
f(x) dx =
f(x) dx +
f(2a – x) dx ………….(1)
Parte 1: Si f(2a – x) = f(x)
Entonces la ecuación (1) se puede escribir como
f(x) dx =
f(x) dx +
f(x) dx
Esto se puede escribir más como
f(x) dx = 2
f(x) dx
Parte 2: Si f(2a – x) = -f(x)
Entonces la ecuación (1) se puede escribir como
f(x) dx=
f(x) dx –
f(x) dx
Esto se puede escribir más como
f(x) dx= 0
Propiedad 7: 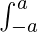 f(x) dx =
f(x) dx =  f(x) dx; si una función es par, es decir, f(-x) = f(x)
f(x) dx; si una función es par, es decir, f(-x) = f(x)
 = 0 ; si una función es impar, es decir, f(-x) = -f(x)
= 0 ; si una función es impar, es decir, f(-x) = -f(x)
Prueba:
De la propiedad 3 podemos escribir
f(x) dx como
f(x) dx =
f(x) dx +
f(x) dx ………(1)
Suponer
f(x) dx = I1 ……(2)
Ahora, suponga que x = -y
Entonces, dx = -dy
Y también cuando x = -a entonces
y= -(-a) = a
y cuando x = 0 entonces, y = 0
Poniendo estos valores en la ecuación (2) obtenemos
I 1 =
f(-y)dy
Usando la propiedad 2, I 1 se puede escribir como
I 1 =
f(-y)dy
y usando la propiedad 1 I 1 se puede escribir como
1 = f(-x) dx
Poniendo el valor de I 1 en la ecuación (1), obtenemos
f(x) dx =
f(-x) dx +
f(x) dx ……….(3)
Parte 1: Cuando f(-x) = f(x)
Entonces la ecuación (3) se convierte en
f(x) dx =
f(x) dx +
f(x) dx
f(x) dx = 2
f(x) dx
Parte 2: Cuando f(-x) = -f(x)
Entonces la ecuación 3 se convierte en
f(x) dx = –
f(x) dx +
f(x) d
f(x)dx = 0
Ejemplos
Ejemplo 1: I = ![]() x(1 – x) 99 dx
x(1 – x) 99 dx
Solución:
Usando la propiedad 4.2, la pregunta dada se puede escribir como
(1 – x) [1 – (1 – x)] 99 dx
(1 – x) [1 – 1 + x] 99 dx
(1 – x)x 99 dx
= 1/100 – 1/101
= 1 / 10100
Ejemplo 2 : I = ![]() cos(x) log
cos(x) log ![]()
Solución:
f(x) = cos(x) log
f(-x) = cos(-x) registro
f(-x) = -cos(x) registro
f(-x) = -f(x)
Por lo tanto la función es impar. Entonces, usando la propiedad
f(x)dx = 0; si una función es impar, es decir, f(-x) = -f(x)
cos(x) log
= 0
Ejemplo 3: I = ![]() [x] dx
[x] dx
Solución:
0 dx +
1 dx +
2 dx +
3 dx +
4 dx [usando la Propiedad 3]
= 0 + [x] 2 1 + 2[x] 3 2 + 3[x] 4 3 + 4[x] 5 4
= 0 + (2 – 1) + 2(3 – 2) + 3(4 – 3) + 4(5 – 4)
= 0 + 1 + 2 + 3 + 4
= 10
Ejemplo 4: I = ![]() |x| dx
|x| dx
Solución:
(-x) dx +
(x) dx [usando la Propiedad 3]
= -[x 2 /2] 0 -1 + [x 2 /2] 2 0
= -[0/2 – 1/2] + [4/2 – 0]
= 1/2 + 2
= 5/2
