Prueba de Durbin Watson: una prueba desarrollada por el profesor de estadística James Durbin y Geoffrey Stuart Watson se utiliza para detectar la autocorrelación en los residuos del análisis de regresión. Se conoce popularmente como estadístico d de Durbin-Watson, que se define como
Primero veamos algunos términos para tener una comprensión clara:
- Análisis de regresión: el análisis de regresión es un conjunto de métodos estadísticos utilizados para estimar las relaciones entre una variable dependiente (Y) y una o más variables independientes (x). Este método ayuda a determinar qué factores influyen más en los resultados y definitivamente deberían estar involucrados en el experimento, y cuáles pueden ignorarse.
- Residuales: es la diferencia entre el valor calculado/observado y el valor pronosticado para una observación en particular. Aquí los residuos están representados por u .
- Autocorrelación: la autocorrelación representa el grado de similitud entre una serie de tiempo determinada y una versión retrasada de sí misma en intervalos de tiempo sucesivos. La autocorrelación mide la relación entre el valor actual de una variable y sus valores pasados. Por ejemplo: los valores de la temperatura del aire se calculan para todos los días de un mes y se observa que el valor del primer día es más similar al valor del segundo día que al valor del trigésimo día. Por lo tanto, se dice que los datos están autocorrelacionados, ya que los valores que se observaron más cerca en el tiempo son más similares que los valores que se observaron más separados.
Supuestos de la prueba d de Durbin-Watson
- Los errores se distribuyen normalmente con un valor medio de 0.
- Los errores son estacionarios.
Hipótesis nula y alternativa de la prueba d de Durbin-Watson
- Hipótesis Nula: No existe autocorrelación de primer orden.
- Hipótesis alternativa: Existe autocorrelación de primer orden.
La hipótesis anterior se formula para verificar la autocorrelación que puede ser positiva o negativa. También podemos comprobar la presencia de autocorrelación positiva y autocorrelación negativa. La hipótesis se formulará en consecuencia.
Estadística de prueba para la prueba d de Durbin-Watson
ut = the residual value for the tth observation. u = Yactual - Ycalculated number of observations in the experiment. d = the ratio of the sum of squared differences in successive residuals to the Residual Sum of Squares(RSS).
Análisis de la estadística d de Durbin-Watson
El valor de d siempre está entre 0 y 4. Si d está cerca de 2 significa que no hay autocorrelación y aceptamos la hipótesis nula. Averiguamos los valores críticos d L y d U para los datos dados. d L es el valor crítico inferior y d U es el valor crítico superior. Usando estos valores, la presencia de autocorrelación se verifica de acuerdo con las reglas de decisión que se mencionan a continuación:
Testing for positive autocorrelation - d < dL = positive autocorrelation is present d > dU = No positive autocorrelation dL < d < dU = Test is inconclusive Testing for positive autocorrelation - 4-d < dL = negative autocorrelation is present 4-d > dU = No negative autocorrelation dL < 4-d < dU = Test is inconclusive
Sobre la base de estas reglas, aceptamos o rechazamos la hipótesis nula.
Pasos para realizar la prueba d de Durbin-Watson
Tomemos un ejemplo para entender cómo realizar esta prueba.
Ejemplo: utilizando los datos de importación y PNB del Reino Unido, pruebe la autocorrelación de los datos aplicando la estadística d de Durbin-Watson. Utilice un nivel de significancia del 5%.
| Importaciones (Y) | 2.6 | 4.1 | 3.5 | 4.3 | 4.5 | 4.2 | 4.1 | 4.5 | 4.9 | 5.2 | 5.4 | 5.3 | 5.2 | 6.2 | 6.4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PNB (X) | 21 | 22 | 22 | 23 | 24 | 24 | 25 | 25 | 25 | 26 | 28 | 29 | 29 | 30 | 32 |
Paso 1: Ejecute el análisis de regresión y obtenga los residuos.
La recta de regresión viene dada por:
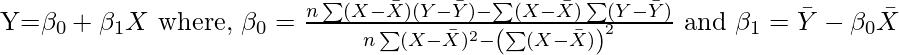
n = total number of observations. Ā = mean value of A. Here A can be X or Y.
Después de calcular la ecuación para la línea de regresión, obtiene los valores calculados de Y correspondientes colocando los valores de X correspondientes. Luego obtenga los valores para los residuos:
Residual(u) = Yactual - Ycalculated for each observation
Paso 2: Calcular el valor de d.
Ahora ponga los valores requeridos y encuentre el valor de d.
Para el ejemplo dado, el valor de d será 1,89.
Paso 3: Averigüe los valores críticos d L y d U .
Para el tamaño de muestra dado (n=15) y el número de variables independientes k (en el ejemplo dado es 1), use la tabla de significancia para encontrar los valores.
El valor de d L es 1.077 y d U es 1.361.
Paso 4: siga las reglas de decisión mencionadas anteriormente para concluir los resultados.
Las reglas que son verdaderas son:
d > dU - No positive autocorrelation 4-d = 2.1 > dU - No negative autocorrelation.
Paso 5: Conclusión de los resultados
Como no hay autocorrelación ni positiva ni negativa aceptamos la hipótesis nula.
Publicación traducida automáticamente
Artículo escrito por shristikotaiah y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA