Multicolinealidad : generalmente ocurre cuando las variables independientes en un modelo de regresión están correlacionadas entre sí. No se espera esta correlación ya que se supone que las variables independientes son independientes. Si el grado de esta correlación es alto, puede causar problemas al predecir los resultados del modelo.
Pocas consecuencias de la multicolinealidad
- Los estimadores tienen varianzas y covarianzas altas, lo que dificulta una estimación precisa.
- Debido a la consecuencia anterior en el punto 1, los intervalos de confianza tienden a hacerse más amplios, lo que lleva a aceptar con más frecuencia la hipótesis cero nula.
- Los errores estándar pueden ser sensibles a pequeños cambios en los datos.
- Los coeficientes se vuelven muy sensibles a pequeños cambios en el modelo. Reduce el poder estadístico del modelo de regresión.
- Los efectos de una sola variable se vuelven difíciles de distinguir de las otras variables.
Entendamos la multicolinealidad con la ayuda de un ejemplo:
Ejemplo: Steve trota mientras escucha música. Cuando escucha música por más tiempo, termina trotando por más tiempo. Ahora queremos determinar la aptitud de Steve. ¿Qué podemos decir, que tendrá un mayor impacto en ella? ¿Escuchar música o hacer footing? En realidad, no podemos decirlo porque estos estimadores tienen una interdependencia entre sí. Si intentamos medir su forma física escuchando música, también está trotando al mismo tiempo y cuando tratamos de medir su forma física trotando, también está escuchando música. Dado que ambos atributos se tomaron como estimadores de su aptitud, es difícil obtener un resultado preciso debido a la presencia de multicolinealidad entre estas variables.
El factor de inflación de varianza (VIF) se utiliza para probar la presencia de multicolinealidad en un modelo de regresión. se define como,
Para un modelo de regresión
dónde,
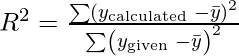
Medida de multicolinealidad
Si el valor de VIF es –
- 1 => no correlacionado. La multicolinealidad no existe.
- Entre 1 y 5 => moderadamente correlacionado. Existe baja multicolinealidad.
- Mayor que 5 => Altamente correlacionado. Existe alta multicolinealidad.
El inverso de VIF se llama Tolerancia y se da como:
- Cuando R 2 = 0, lo que significa que no hay colinealidad, podemos decir que la tolerancia es alta (=1).
Luego puede usar otras técnicas para resolver este problema de multicolinealidad si la extensión es demasiado alta.
Para cualquier consulta deja un comentario abajo.
Publicación traducida automáticamente
Artículo escrito por shristikotaiah y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA