Si en la prueba ANOVA llegamos a la conclusión de que tenemos que rechazar nuestra hipótesis nula (H 0 ) y luego sabemos que las medias de algún tratamiento o nivel de factor son diferentes y deseamos encontrarlas, entonces procedemos a hacer un análisis post hoc con Tukey. prueba para encontrar qué par es diferente. Este método es un método de comparación múltiple.
Sobre:
- Se utiliza para hablar sobre la población significa tener una diferencia significativa.
- Realizado cuando H 0 es rechazada por el método ANOVA.
- Necesitamos hacer comparaciones por pares en este método.
- Utiliza el rango crítico para comparar las diferencias medias absolutas.
Fórmula de rango crítico:
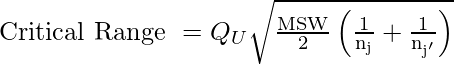
Pasos:
- Calcule las diferencias medias absolutas para todos los pares posibles.
- Encuentre el valor Q u de la tabla estándar.
- Calcule el rango crítico a partir de la fórmula mencionada anteriormente.
- Compare con los resultados obtenidos en el paso 1.
Ejemplo:
Una empresa de frutas quería saber la cantidad perfecta de pulpa de fruta para su jugo, por lo que realizó una encuesta y pidió a los consumidores que calificaran su sabor en una escala de 0 a 25. Tenga en cuenta que el sabor no depende de la cantidad de pulpa de fruta, depende de la pulpa artificial.
Los siguientes fueron los resultados inferidos:
| Pulpa (%) | Observaciones | Total | Promedio | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| 5 | 7 | 8 | 15 | 11 | 9 | 10 | 60 | 10.00 |
| 10 | 12 | 17 | 13 | 18 | 19 | 15 | 94 | 15.67 |
| 15 | 14 | 18 | 19 | 17 | dieciséis | 18 | 102 | 17.00 |
| 20 | 19 | 25 | 22 | 23 | 18 | 20 | 127 | 21.17 |
| 383 | 15.96 | |||||||
Paso 1: Cálculo de las diferencias medias absolutas:

Paso 2:
Aquí, C = 4 y NC = 24 – 4 = 20
Sea α = 0.05
De la tabla Q estándar Q u = 3.96
Paso 3: Poner el valor obtenido arriba obtenemos Rango Crítico = 4.124
Paso 4: Compárelo con todos los resultados del Paso 1, obtenemos que todas las diferencias medias absolutas son mayores que el rango crítico. Aparte de ( X 2 , X 3 ). Por lo tanto, vemos una diferencia significativa entre cada par de medias, excepto la concentración del 10 % y la concentración del 15 % en el nivel de significancia del 5 %.
Publicación traducida automáticamente
Artículo escrito por parthbanathia y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA