Dada una array bidimensional A de ceros y unos y un número entero K .
En cada movimiento, puede elegir cualquier fila o columna y alternar cada valor en esa fila o columna. Es decir, cambie todos los 0 por 1 o todos los 1 por 0 . Después de hacer como máximo K movimientos, cada fila de esta array representa un número binario.
La tarea es devolver el valor máximo posible de la suma de estos números.
Ejemplos :
Input : A[][] = { { 0, 0, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 0 } };
K = 2
Output : 36
Input : A[][] = { { 0, 1 },
{ 1, 0 },
{ 1, 1 } };
K = 1
Output : 7
Observe que un 1 en la i -ésima columna de la derecha contribuye con 2i a la puntuación.
También sabiendo el hecho de que ![]() , maximizar el dígito más a la izquierda es más importante que cualquier otro dígito. Por lo tanto, cualquier fila debe alternarse de manera que la columna más a la izquierda sea todo 0 o todo 1 (de modo que después de alternar la columna más a la izquierda [si es necesario], la columna de la izquierda sea todo 1 ).
, maximizar el dígito más a la izquierda es más importante que cualquier otro dígito. Por lo tanto, cualquier fila debe alternarse de manera que la columna más a la izquierda sea todo 0 o todo 1 (de modo que después de alternar la columna más a la izquierda [si es necesario], la columna de la izquierda sea todo 1 ).
Ahora, para las filas con el primer elemento como 0, haga un mapa con el valor de la fila como clave y el índice de esa fila como elemento. Ahora alternamos las filas con el menor valor para que, después de actualizar, contribuya al máximo a nuestra puntuación total.
Ahora, para otras columnas posteriores contamos el total de ceros y unos .
- Si ( ceros > unos y K > 0 ) alternamos la columna y actualizamos nuestra respuesta a ans = ans + zero * pow( 2, column – j – 1) , para todos
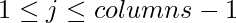 y decrementa K en uno.
y decrementa K en uno. - De lo contrario, actualizamos la respuesta a ans = ans + one * pow (2, columnas – j – 1) , para todos
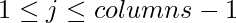 .
.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to find the maximum score after
// flipping a Binary Matrix atmost K times
#include <bits/stdc++.h>
using namespace std;
const int n = 3;
const int m = 4;
// Function to find maximum score of matrix
int maxMatrixScore(int A[n][m], int K)
{
map<int, int> update;
// find value of rows having first
// column value equal to zero
for (int i = 0; i < n; ++i) {
if (A[i][0] == 0) {
int ans = 0;
for (int j = 1; j < m; ++j)
ans = ans + A[i][j] * pow(2, m - j - 1);
update[ans] = i;
}
}
// update those rows which lead to
// maximum score after toggle
map<int, int>::iterator it = update.begin();
while (K > 0 && it != update.end()) {
int idx = it->second;
for (int j = 0; j < m; ++j)
A[idx][j] = (A[idx][j] + 1) % 2;
it++;
K--;
}
// Calculating answer
int ans = 0;
for (int j = 0; j < m; ++j) {
int zero = 0, one = 0;
for (int i = 0; i < n; ++i) {
A[i][j] == 0 ? zero++ : one++;
}
// check if K > 0 we can toggle if necessary.
if (K > 0 && zero > one) {
ans += zero * pow(2, m - j - 1);
K--;
}
else
ans += one * pow(2, m - j - 1);
}
// return max answer possible
return ans;
}
// Driver program
int main()
{
int A[n][m] = { { 0, 0, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 0 } };
int K = 2;
// function call to print required answer
cout << maxMatrixScore(A, K);
return 0;
}
Java
// Java program to find the maximum score after
// flipping a Binary Matrix atmost K times
import java.util.*;
class GFG
{
static int n = 3;
static int m = 4;
// Function to find maximum score of matrix
static int maxMatrixScore(int A[][], int K)
{
HashMap<Integer,Integer> update =
new HashMap<Integer,Integer>();
// find value of rows having first
// column value equal to zero
for (int i = 0; i < n; ++i)
{
if (A[i][0] == 0)
{
int ans = 0;
for (int j = 1; j < m; ++j)
ans = (int) (ans + A[i][j] *
Math.pow(2, m - j - 1));
update.put(ans, i);
}
}
// Update those rows which lead to
// maximum score after toggle
for (Map.Entry<Integer,Integer> it : update.entrySet())
if (K > 0 )
{
int idx = it.getValue();
for (int j = 0; j < m; ++j)
A[idx][j] = (A[idx][j] + 1) % 2;
K--;
}
// Calculating answer
int ans = 0;
for (int j = 0; j < m; ++j)
{
int zero = 0, one = 0;
for (int i = 0; i < n; ++i)
{
if(A[i][j] == 0)
zero++;
else
one++;
}
// Check if K > 0 we can toggle if necessary.
if (K > 0 && zero > one)
{
ans += zero * Math.pow(2, m - j - 1);
K--;
}
else
ans += one * Math.pow(2, m - j - 1);
}
// return max answer possible
return ans;
}
// Driver code
public static void main(String[] args)
{
int A[][] = { { 0, 0, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 0 } };
int K = 2;
// function call to print required answer
System.out.print(maxMatrixScore(A, K));
}
}
// This code is contributed by PrinciRaj1992
Python3
# Python3 program to find the maximum
# score after flipping a Binary Matrix
# atmost K times
n = 3
m = 4
# Function to find maximum score of matrix
def maxMatrixScore(A, K):
update = {}
# Find value of rows having first
# column value equal to zero
for i in range(0, n):
if A[i][0] == 0:
ans = 0
for j in range(1, m):
ans = ans + A[i][j] * 2 ** (m - j - 1)
update[ans] = i
# update those rows which lead to
# maximum score after toggle
for idx in update.values():
for j in range(0, m):
A[idx][j] = (A[idx][j] + 1) % 2
K -= 1
if K <= 0:
break
# Calculating answer
ans = 0
for j in range(0, m):
zero, one = 0, 0
for i in range(0, n):
if A[i][j] == 0: zero += 1
else: one += 1
# check if K > 0 we can
# toggle if necessary.
if K > 0 and zero > one:
ans += zero * 2 ** (m - j - 1)
K -= 1
else:
ans += one * 2 ** (m - j - 1)
# return max answer possible
return ans
# Driver Code
if __name__ == "__main__":
A = [[0, 0, 1, 1],
[1, 0, 1, 0],
[1, 1, 0, 0]]
K = 2
# function call to print required answer
print(maxMatrixScore(A, K))
# This code is contributed by Rituraj Jain
C#
// C# program to find the maximum score after
// flipping a Binary Matrix atmost K times
using System;
using System.Collections.Generic;
class GFG
{
static int n = 3;
static int m = 4;
// Function to find maximum score of matrix
static int maxMatrixScore(int [,]A, int K)
{
Dictionary<int,int> update =
new Dictionary<int,int>();
// find value of rows having first
// column value equal to zero
int ans=0;
for (int i = 0; i < n; ++i)
{
if (A[i, 0] == 0)
{
ans = 0;
for (int j = 1; j < m; ++j)
ans = (int) (ans + A[i, j] *
Math.Pow(2, m - j - 1));
update.Add((int)ans, i);
}
}
// Update those rows which lead to
// maximum score after toggle
foreach(KeyValuePair<int, int> it in update)
if (K > 0 )
{
int idx = it.Value;
for (int j = 0; j < m; ++j)
A[idx, j] = (A[idx, j] + 1) % 2;
K--;
}
// Calculating answer
ans = 0;
for (int j = 0; j < m; ++j)
{
int zero = 0, one = 0;
for (int i = 0; i < n; ++i)
{
if(A[i, j] == 0)
zero++;
else
one++;
}
// Check if K > 0 we can toggle if necessary.
if (K > 0 && zero > one)
{
ans += zero * (int)Math.Pow(2, m - j - 1);
K--;
}
else
ans += one * (int)Math.Pow(2, m - j - 1);
}
// return max answer possible
return ans;
}
// Driver code
public static void Main(String[] args)
{
int [,]A = { { 0, 0, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 0 } };
int K = 2;
// function call to print required answer
Console.Write(maxMatrixScore(A, K));
}
}
// This code is contributed by 29AjayKumar
Javascript
<script>
// Javascript program to find the maximum score after
// flipping a Binary Matrix atmost K times
var n = 3;
var m = 4;
// Function to find maximum score of matrix
function maxMatrixScore(A, K)
{
var update = new Map();
// find value of rows having first
// column value equal to zero
for (var i = 0; i < n; ++i) {
if (A[i][0] == 0) {
var ans = 0;
for (var j = 1; j < m; ++j)
ans = ans + A[i][j] * Math.pow(2, m - j - 1);
update.set(ans, i);
}
}
// update those rows which lead to
// maximum score after toggle
update.forEach((value, key) => {
if(K>0)
{
var idx = value;
for (var j = 0; j < m; ++j)
A[idx][j] = (A[idx][j] + 1) % 2;
K--;
}
});
// Calculating answer
var ans = 0;
for (var j = 0; j < m; ++j) {
var zero = 0, one = 0;
for (var i = 0; i < n; ++i) {
A[i][j] == 0 ? zero++ : one++;
}
// check if K > 0 we can toggle if necessary.
if (K > 0 && zero > one) {
ans += zero * Math.pow(2, m - j - 1);
K--;
}
else
ans += one * Math.pow(2, m - j - 1);
}
// return max answer possible
return ans;
}
// Driver program
var A = [ [ 0, 0, 1, 1 ],
[ 1, 0, 1, 0 ],
[ 1, 1, 0, 0 ] ];
var K = 2;
// function call to print required answer
document.write( maxMatrixScore(A, K));
// This code is contributed by noob2000.
</script>
36
Complejidad de tiempo: O(N*M)
Espacio Auxiliar: O(N)
Publicación traducida automáticamente
Artículo escrito por Sanjit_Prasad y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA