Puntos máximos de intersecciones posibles entre X círculos y Y rectas

Dados dos enteros X e Y , la tarea es encontrar el máximo número de puntos de intersección posibles entre X círculos y Y rectas.

Ejemplo:  

Entrada: X = 4, Y = 4 
Salida: 50 
Explicación: 
4 líneas se intersecan entre sí en 6 puntos y 4 círculos se intersecan entre sí en un máximo de 12 puntos. 
Cada línea corta 4 círculos en 8 puntos. 
Por lo tanto, 4 líneas intersecan cuatro círculos en un máximo de 32 puntos. 
Por lo tanto, número requerido de intersecciones = 6 + 12 + 32 = 50.

Entrada: X = 3, Y = 4 
Salida: 36 
 

Aproximación: 
Se puede observar que existen tres tipos de intersecciones:  

1. El número de formas de elegir un par de puntos de X círculos es 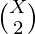 . Cada uno de estos pares se cruzan como máximo en dos puntos.
2. El número de formas de elegir un par de puntos de las líneas Y es  . Cada uno de estos pares se cruzan en un punto como máximo.
3. El número de formas de elegir un círculo y una línea de X círculos y líneas Y es 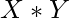 . Cada uno de estos pares se cruzan en dos puntos como máximo. 

Entonces, el número máximo de puntos de intersección se puede calcular como: 
=> 
=> 
 

Por lo tanto, la fórmula para encontrar el número máximo de puntos de intersección de X círculos y Y rectas es: 

A continuación se muestra la implementación del enfoque anterior:  

// C++ program to implement
// the above approach
#include <bits/stdc++.h>
using namespace std;
 
int maxPointOfIntersection(int x, int y)
{
    int k = y * (y - 1) / 2;
    k = k + x * (2 * y + x - 1);
    return k;
}
 
// Driver code
int main()
{
     
    // Number of circles
    int x = 3;
     
    // Number of straight lines
    int y = 4;
 
    // Function Call
    cout << (maxPointOfIntersection(x, y));
}
 
// This code is contributed by Ritik Bansal

// Java program to implement
// the above approach
class GFG{
     
static int maxPointOfIntersection(int x, int y)
{
    int k = y * (y - 1) / 2;
    k = k + x * (2 * y + x - 1);
    return k;
}
 
// Driver code
public static void main(String[] args)
{
     
    // Number of circles
    int x = 3;
     
    // Number of straight lines
    int y = 4;
 
    // Function Call
    System.out.print(maxPointOfIntersection(x, y));
}
}
 
// This code is contributed by Princi Singh

# Python3 program to implement
# the above approach
def maxPointOfIntersection(x, y):
    k = y * ( y - 1 ) // 2
    k = k + x * ( 2 * y + x - 1 )
    return k
 
# Number of circles
x = 3
# Number of straight lines
y = 4
 
# Function Call
print(maxPointOfIntersection(x, y))

// C# program to implement
// the above approach
using System;
 
class GFG{
     
static int maxPointOfIntersection(int x, int y)
{
    int k = y * (y - 1) / 2;
    k = k + x * (2 * y + x - 1);
    return k;
}
 
// Driver code
public static void Main(String[] args)
{
     
    // Number of circles
    int x = 3;
     
    // Number of straight lines
    int y = 4;
 
    // Function Call
    Console.Write(maxPointOfIntersection(x, y));
}
}
 
// This code is contributed by Princi Singh

<script>
 
// Javascript program to implement
// the above approach
function maxPointOfIntersection(x, y)
{
    let k = y * (y - 1) / 2;
    k = k + x * (2 * y + x - 1);
    return k;
}
 
// Driver code
 
// Number of circles
let x = 3;
   
// Number of straight lines
let y = 4;
 
// Function Call
document.write(maxPointOfIntersection(x, y));
 
// This code is contributed by rameshtravel07
 
</script>

36

Tiempo Complejidad: O(1)  
Espacio Auxiliar: O(1)