Rompecabezas: Encuentre todos los valores de N para los cuales se puede dividir un cuadrado en N cuadrados más pequeños y describa un algoritmo para hacer tal disección.
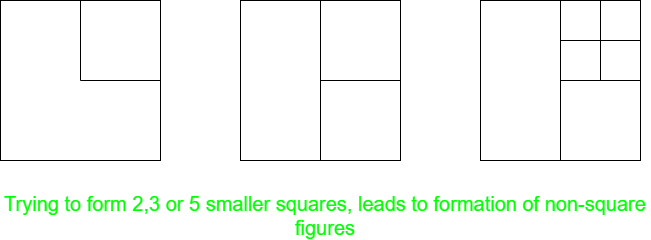
Solución: El punto básico a observar es un cuadrado que tiene 4 ángulos rectos. Entonces, para dividirlo en cuadrados más pequeños, cada uno de sus ángulos rectos debe caer en otro cuadrado, ya que más de un ángulo recto juntos darán como resultado figuras no cuadradas.
Ahora, considere los siguientes casos:
- Cuando N = 2, 3 o 5: No es posible tal división , ya que viola la condición anterior y se obtienen figuras sin forma.
- Cuando N = 4: Este es el caso más fácil. Simplemente divida el cuadrado horizontal y verticalmente, desde el centro . La figura resultante tendrá 4 cuadrados.
- Cuando N es par y mayor que 4: Este caso puede generalizarse considerando N = 2k y formando 2k – 1 , cuadrados iguales a lo largo de los lados adyacentes del cuadrado dado. Sin embargo, la longitud del lado de cada cuadrado más pequeño debe ser igual a 1/k de la longitud del cuadrado dado.
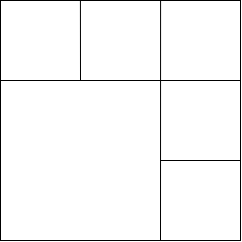
Por ejemplo: Considere el ejemplo cuando N = 6 como se muestra en la figura, aquí hemos formado 5 cuadrados a lo largo de la parte superior y del lado derecho, cada uno de los lados (1/3) del lado del cuadrado original. Además, queda un cuadrado de lado (2/k) , lo que da como resultado un total de 6 cuadrados.
- Caso N es impar y mayor que 5: este caso se basa en la solución para valores pares de N . Si N es impar, podemos descomponerlo como N = 2k + 1 , que además se puede escribir como N = 2(k – 1) + 3 . Ahora, primero podemos formar 2(k – 1) cuadrados utilizando el método anterior y luego dividir uno de los cuadrados obtenidos en cuatro cuadrados más pequeños, lo que aumentará el total de cuadrados en 3.
Por ejemplo: Considere el ejemplo cuando N = 9 como se muestra. Aquí, primero formamos 6 cuadrados y luego dividimos el cuadrado superior izquierdo en 4 cuadrados más pequeños, para obtener un total de 9 cuadrados.
Publicación traducida automáticamente
Artículo escrito por CharchitKapoor y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA