Requisito previo: regresión lineal La regresión lineal es un algoritmo de aprendizaje automático basado en el aprendizaje supervisado. Realiza una tarea de regresión. La regresión modela un valor de predicción objetivo basado en variables independientes. Se utiliza principalmente para averiguar la relación entre las variables y la previsión. Los diferentes modelos de regresión difieren según el tipo de relación entre las variables dependientes e independientes que están considerando y la cantidad de variables independientes que se utilizan. Este artículo demostrará cómo usar las diversas bibliotecas de Python para implementar la regresión lineal en un conjunto de datos determinado. Demostraremos un modelo lineal binario ya que será más fácil de visualizar. En esta demostración, el modelo utilizará Gradient Descent para aprender. Puedes aprender sobre esto aquí.
Paso 1: Importación de todas las bibliotecas requeridas
Python3
import numpy as np import pandas as pd import seaborn as sns import matplotlib.pyplot as plt from sklearn import preprocessing, svm from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression
Paso 2: Lectura del conjunto de datos Puede descargar el conjunto de datos
Python3
df = pd.read_csv('bottle.csv')
df_binary = df[['Salnty', 'T_degC']]
# Taking only the selected two attributes from the dataset
df_binary.columns = ['Sal', 'Temp']
#display the first 5 rows
df_binary.head()
Producción:
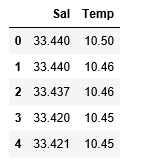
Paso 3: Explorando la dispersión de datos
Python3
#plotting the Scatter plot to check relationship between Sal and Temp sns.lmplot(x ="Sal", y ="Temp", data = df_binary, order = 2, ci = None)
Producción:
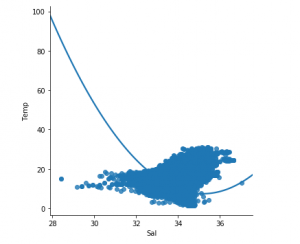
Paso 4: limpieza de datos
Python3
# Eliminating NaN or missing input numbers df_binary.fillna(method ='ffill', inplace = True)
Paso 5: Entrenando nuestro modelo
Python3
X = np.array(df_binary['Sal']).reshape(-1, 1) y = np.array(df_binary['Temp']).reshape(-1, 1) # Separating the data into independent and dependent variables # Converting each dataframe into a numpy array # since each dataframe contains only one column df_binary.dropna(inplace = True) # Dropping any rows with Nan values X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25) # Splitting the data into training and testing data regr = LinearRegression() regr.fit(X_train, y_train) print(regr.score(X_test, y_test))
Producción:
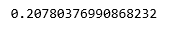
Paso 6: Explorando nuestros resultados
Python3
y_pred = regr.predict(X_test) plt.scatter(X_test, y_test, color ='b') plt.plot(X_test, y_pred, color ='k') plt.show() # Data scatter of predicted values
Producción:
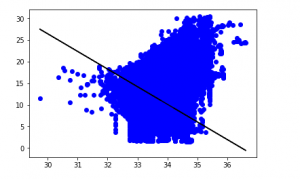
El bajo puntaje de precisión de nuestro modelo sugiere que nuestro modelo regresivo no se ha ajustado muy bien con los datos existentes. Esto sugiere que nuestros datos no son adecuados para la regresión lineal. Pero a veces, un conjunto de datos puede aceptar un regresor lineal si consideramos solo una parte de él. Comprobemos esa posibilidad.
Paso 7: trabajar con un conjunto de datos más pequeño
Python3
df_binary500 = df_binary[:][:500] # Selecting the 1st 500 rows of the data sns.lmplot(x ="Sal", y ="Temp", data = df_binary500, order = 2, ci = None)
Producción:
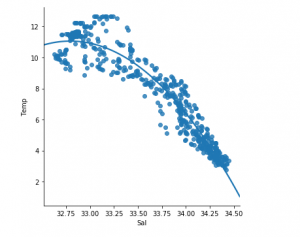
Ya podemos ver que las primeras 500 filas siguen un modelo lineal. Continuando con los mismos pasos que antes.
Python3
df_binary500.fillna(method ='ffill', inplace = True) X = np.array(df_binary500['Sal']).reshape(-1, 1) y = np.array(df_binary500['Temp']).reshape(-1, 1) df_binary500.dropna(inplace = True) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25) regr = LinearRegression() regr.fit(X_train, y_train) print(regr.score(X_test, y_test))
Producción:
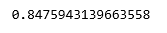
Python3
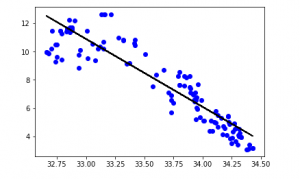
y_pred = regr.predict(X_test) plt.scatter(X_test, y_test, color ='b') plt.plot(X_test, y_pred, color ='k') plt.show()
Producción:
Paso 8: Métricas de evaluación para regresión
Por último, comprobamos el rendimiento del modelo de regresión lineal con la ayuda de métricas de evaluación. Para los algoritmos de regresión, usamos ampliamente las métricas mean_absolute_error y mean_squared_error para verificar el rendimiento del modelo.
Python3
from sklearn.metrics import mean_absolute_error,mean_squared_error
mae = mean_absolute_error(y_true=y_test,y_pred=y_pred)
#squared True returns MSE value, False returns RMSE value.
mse = mean_squared_error(y_true=y_test,y_pred=y_pred) #default=True
rmse = mean_squared_error(y_true=y_test,y_pred=y_pred,squared=False)
print("MAE:",mae)
print("MSE:",mse)
print("RMSE:",rmse)
Producción:
MAE: 0.7927322046360309 MSE: 1.0251137190180517 RMSE: 1.0124789968281078
Publicación traducida automáticamente
Artículo escrito por AlindGupta y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA