¿Qué medida de tendencia central está asociada con las ojivas?

En datos estadísticos, el resumen descriptivo de un conjunto de datos se conoce como tendencia central. Se considera que es un indicador del centro de la distribución de datos. En resumen, representa el valor único de toda la distribución o un conjunto de datos. Describe los datos con precisión. 

Sin embargo, la tendencia central de la distribución de datos no proporciona información sobre datos individuales del conjunto de datos. Hay varias medidas de la tendencia central de los datos. 

Medidas de tendencia central 

Como describimos, la tendencia central de los datos como un indicador de los valores, describiendo el conjunto de datos calculando la posición central de los datos. La tendencia central de los datos se puede medir por las siguientes cantidades: 

• Media: Se considera que la media es la suma de todas las observaciones dividida por el número total de observaciones.
• Mediana: La mediana se define como el valor medio o central en un conjunto ordenado.
• Moda: La moda se define como el valor que ocurre con mayor frecuencia en un conjunto de datos.

Ojiva

La ojiva de una distribución de datos particular se define como el gráfico de distribución de frecuencia de una serie. La ojiva para cualquier distribución acumulativa se puede construir como un gráfico que explica los valores de los datos en el eje del plano horizontal. Incluso puede representar las frecuencias acumuladas o las frecuencias relativas, o incluso las frecuencias porcentuales acumuladas en el eje vertical.

Por ejemplo, la popularidad de una determinada distribución de datos dentro de un cierto rango de frecuencia se puede trazar fácilmente con la curva Ogive, que ayuda a encontrar esos detalles con mucha precisión. Por lo tanto, se utiliza para hacer una precisión precisa sobre la probabilidad de los datos. 

La Ojiva se construye trazando el punto correspondiente a la frecuencia acumulada de cada intervalo de clase. Se representa en forma pictórica. Básicamente proporciona una estimación del número de observaciones que son menos que iguales a un valor específico dado. 

Tipos de ojiva 

Ojiva se define como el total de frecuencias que se muestran en forma de tabla distribuida en intervalos de clase. Hay básicamente dos tipos diferentes de ojiva, es decir, menor que y mayor que. 

menor que la ojiva

En la ojiva menor que se obtiene y representa un gráfico sumando sucesivamente las frecuencias pertenecientes a todas las clases anteriores. También incluye la clase a la que pertenece. Este tipo de ojiva tiene el número de observaciones menor que el límite de la clase superior. Comenzamos la acumulación desde el menor alcance hasta el mayor tamaño. 

mayor que la ojiva

También conocida como ojiva de más que tipo, este tipo de ojiva tiene el número de observaciones mayor o igual que el límite menor de la clase. Este tipo de ojiva es el reverso de menor que la ojiva. Se puede obtener calculando el total acumulativo de frecuencias que comienza en la clase más alta y llega a la más baja.

Construcción de un gráfico de ojiva 

Una forma visual simple de representar y trazar las frecuencias acumuladas que pertenecen a diferentes valores o categorías es parte de la construcción de un gráfico de ojiva. Hay varios pasos involucrados en la construcción de un gráfico de ojiva: 

1. Se calcula una tabla de distribución de frecuencias de una longitud de clase adecuada utilizando las variables continuas.
2. Se calcula la frecuencia para cada intervalo de clase.
3. Se calcula el punto final para cada intervalo de clase. (límite superior o límite inferior).
4. Los números se agregan en la columna de frecuencia para calcular la frecuencia acumulada de la distribución de datos.
5. Almacene los resultados en un formato tabular.

Usos de la curva de ojiva 

Ogive Graph o los gráficos de frecuencia acumulada se utilizan para encontrar la mediana del conjunto de datos dado. Si ambos, menor que y mayor que, la curva de frecuencia acumulada se dibuja en el mismo gráfico, podemos encontrar fácilmente el valor medio. El punto de intersección de ambas curvas, correspondiente al eje x, da el valor de la mediana. Además de encontrar las medianas, las ojivas se utilizan para calcular los percentiles de los valores del conjunto de datos.

Mediana

La mediana de un conjunto de datos o distribución de datos se define como el número central o un valor central en el conjunto. La mediana es la media en orden ascendente de los datos ordenados. La mediana es el promedio calculado en datos ordenados. La mediana da una medida de la tendencia central de los datos en caso de que los datos ya estén disponibles en orden ascendente. Se puede considerar como un indicador del centro de la distribución de datos.

Sin embargo, la mediana de los datos da una pequeña estimación sobre la disposición de los datos, lo que significa que los valores a la izquierda de la mediana son más pequeños y, de manera similar, los valores a la derecha de la media son más grandes que la mediana. La mediana del conjunto de datos puede no ser única. 

Para calcular la mediana de la distribución de datos dada, el conjunto de datos primero se clasifica en orden ascendente manualmente. Los datos ahora están ordenados en los valores que comienzan desde el valor más bajo hasta el más alto. Se puede considerar que una mediana es un número que está separado por la mitad superior de una muestra de datos, de la mitad inferior. La mediana varía para los diferentes tipos de distribución de datos. Para un número impar de observaciones, la mediana de los datos es el valor medio de los datos ordenados. Para un conjunto de datos con un número par de observaciones, la mediana es el promedio de los dos valores centrales. 

Por ejemplo, la mediana de los valores de datos dados, 3, 3, 5, 9, 11 es 5. Dado que hay un número par de observaciones, la mediana es equivalente a la media o promedio de los dos valores centrales, por lo tanto, la mediana de 3, 5, 7, 9 es (5+7)/2 = 6.

Para encontrar la mediana en la ojiva, siga estos pasos:

1. Todos los puntos se trazan y luego se unen correspondientemente con líneas.
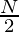2.  Se calcula el valor de  .
3. El valor está marcado en la escala de frecuencia acumulada (eje y).
4. Este valor se une a la línea que se forma trazando los puntos con líneas de puntos.
5. Conecte este punto al punto del eje x usando una línea de puntos recta.
6. El punto de intersección es la mediana.

Ejemplos de preguntas

Pregunta 1. Calcule la mediana de los siguientes datos:

2, 5, 7, 3, 11, 9, 12, 4, 1, 15, 2.

Solución:

Para encontrar la mediana de los datos, tenemos, 

Organizar los datos en orden ascendente

1, 2, 2, 3, 4, 5, 7, 9, 11, 12, 15

Hay un total de 11 números en la distribución de datos. 

La mediana es el sexto ^número . 

Por lo tanto, la mediana es 5.

El valor mediano de este conjunto de números es 24.

Pregunta 2. ¿Cómo se calcula la mediana de dos números? 

Solución:

Como tenemos un número par de observaciones, tenemos,

es decir, mediana = 

Por ejemplo: Para calcular la mediana de los números 12 y 17 es: 

Pregunta 3. ¿Diferenciar entre media y mediana?

Solución: 

Significar	Mediana
La aritmética promedio de un conjunto dado de números	El método de separar la muestra más alta con el valor más bajo de una distribución de probabilidad
Se utiliza para distribuciones normales.	Se utiliza para distribuciones sesgadas.
Hay muchos factores externos que limitan el uso de Mean.	Es mucho más robusto y confiable para medir los datos de datos desiguales.
se calcula sumando todos los valores y dividiendo el total por el número de valores.	se calcula enumerando todos los números disponibles en el conjunto al organizar el orden y luego encontrando el número en el centro de la distribución.
media aritmética.	media posicional.
Es muy sensible a los datos atípicos.	No es muy sensible a los datos atípicos.

Pregunta 4. ¿Ilustrar las 4 medidas de tendencia central? 

Solución: 

Las cuatro medidas de tendencia central son la media, la mediana, la moda y el rango medio. Aquí, el rango medio o extremo medio de un conjunto de valores de datos estadísticos es la media aritmética de los valores máximo y mínimo en un conjunto de datos.

Pregunta 5. ¿Cómo encuentras la tendencia central? 

Solución: 

La tendencia central se puede calcular utilizando la media, la mediana (el valor más medio) o la moda (el valor más frecuente) en el conjunto de datos.