Las ecuaciones cuadráticas son las ecuaciones donde el polinomio tiene el grado dos. Las ecuaciones cuadráticas son las ecuaciones del tipo ax 2 + bx + c = 0 donde x es desconocido y a, b, c son números reales conocidos y a no debe ser cero. Si a=0 entonces la ecuación no permanecerá cuadrática, será entonces lineal ya que a=0 eliminará x 2 término. Como la ecuación cuadrática tiene el mayor grado dos, entonces esta ecuación tiene dos raíces, o podemos decir que encontraremos dos valores de x para una ecuación cuadrática.
¿Cómo encontrar las raíces?
Método 1: Las raíces de las ecuaciones cuadráticas se pueden encontrar mediante la fórmula Shridharacharaya.
x = [-b±√(b 2 – 4ac)]/2a
Ejemplo: La longitud de los lados de un rectángulo está dada por x – 3 y x – 5 y el área del rectángulo es 3 unidad 2 . Encuentra los lados del rectángulo.
Solución:
Área del rectángulo = largo*ancho = (x – 3)(x – 5) = 3
Área = x 2 – 8x + 15 = 3
= x 2 – 8x + 12 = 0
Discriminante = b 2 – 4ac = 64 – (4(1)(12)) = 64 – 48 = 16
x = [-b ± √(b 2 -4ac)]/2a = [-(-8) ± √16]/2 = (8±4)/2
x = 12/2 o 4/2
x = 2 o 6
Cuando x es 2, los lados son x – 3 = 2 – 3 = -1 y x – 5 = 2 – 5 = -3.
Dado que la longitud de los lados no puede ser igual, x = 2 no es una respuesta válida.
Cuando x es 6, los lados son x – 3 = 6 – 3 = 3 y x – 5= 6 – 5 =1.
Por lo tanto, x = 6 es la respuesta válida y los lados son 3 y 1.
Método 2. La otra forma es el método de factorización. Una ecuación cuadrática puede considerarse un factor de dos términos. Como ax 2 + bx + c = 0 se puede escribir como (x – x 1 )(x – x 2 ) = 0 donde x 1 y x 2 son raíces de la ecuación cuadrática.
Pasos:
- Encuentre dos números tales que allí producto = ac y allí suma = b.
- Luego escribe el coeficiente x como la suma de estos dos números y divídelos de manera que obtengas dos términos para x.
- factorizar los dos primeros como grupo y los dos últimos términos como grupo.
- Tome los factores comunes de estos y al igualar las dos expresiones con cero después de tomar los factores comunes y reorganizar la ecuación obtenemos las raíces.
Ejemplo: Sea la ecuación cuadrática x 2 + 3x = 18
x2 + 3x – 18 = 0
Paso:
1. 6 y -3 son los números cuya suma es igual a b y el producto es igual a ac.
2. x2 + (6-3)x – 18 = x2 + 6x -3x – 18 =0
3. x(x + 6) – x(x + 6) = 0
4. tomando (x + 6) como común.
(x + 6)(x – 3) = 0
x = -6 o x = 3
En un método de factorización no es necesario que siempre encuentres fácilmente estos dos números (especialmente en el caso de que las raíces sean imaginarias o irracionales), por lo que es mejor usar la fórmula cuadrática.
Naturaleza de las raíces
La naturaleza de las raíces depende del discriminante de la ecuación cuadrática. El discriminante de una ecuación cuadrática está dado por b 2 – 4ac. Es así porque en la fórmula cuadrática está la raíz cuadrada del discriminante.
Raíz 1: Si b 2 – 4ac > 0 raíces son reales y diferentes. Como el discriminante es >0, su raíz cuadrada no será imaginaria. Tiene dos casos.
- Si b 2 – 4ac es un cuadrado perfecto, entonces las raíces son racionales. Como el discriminante es un cuadrado perfecto, entonces tendremos un número entero como raíz cuadrada del discriminante. Por lo tanto, las raíces son números racionales.
Ejemplo: Sea la ecuación cuadrática x 2 -5x+6=0.
Entonces el discriminante de la ecuación dada es b 2 – 4ac=(-5) 2 – 4*1*6 = 25-24 = 1
Según la fórmula Shridharacharaya
x = [-b±√(b 2 -4ac)]/2a = x = [-(-5) ± √1]/2
x1 = [-(- 5 ) + √1]/2 = 6/2 = 3
x2 = [-(-5) – √1]/2 = 4/2 = 2
Por lo tanto, las raíces son 3,2. Ambos son racionales y diferentes.
- Si b 2 – 4ac no es un cuadrado perfecto, entonces la raíz cuadrada del discriminante es irracional, por lo tanto, las raíces son irracionales y ocurren en pares.
Ejemplo: Sea la ecuación cuadrática x 2 -7x+8 = 0.
Entonces el discriminante de la ecuación dada es
b 2 – 4ac=(-7) 2 – 4*1*8 = 49-32 = 17
Según la fórmula Shridharacharaya
x = [-b±√(b 2 -4ac)]/2a = x = [-(-7) ± √17]/2
x1 = [-(- 7 ) + √17]/2 = [7 + √17]/2
x2 = [-(-7) – √17]/2 = [7 – √17]/2
Por lo tanto, las raíces son [7 + √17]/2,[7 – √17]/2. Ambos son irracionales y en parejas.
Raíz 2: Si b 2 – 4ac = 0 raíces son reales e iguales.
Ejemplo: Sea la ecuación cuadrática 3x 2 -6x+3=0.
Entonces el discriminante de la ecuación dada es
b 2 – 4ac=(-6) 2 – 4*3*3 = 36 – 36 = 0
Según la fórmula Shridharacharaya
x = [-b±√(b 2 -4ac)]/2a = x = [-(-6) ± √0]/[(2)(3)]
x1 = [-(-6) + √0]/2 = 6/6 = 1
x2 = [-(-6) – √0]/2 = 6/6 = 1
Por lo tanto, las raíces son 1,1. Ambos son reales e iguales.
Raíz 3: Si b 2 – 4ac < 0 las raíces son imaginarias, o puedes decir raíces complejas. Es imaginario porque el término debajo de la raíz cuadrada es negativo. Estas raíces complejas siempre aparecerán en pares, es decir, ambas raíces son conjugadas entre sí.
Ejemplo: Sea la ecuación cuadrática x 2 +6x+11=0.
Entonces el discriminante de la ecuación dada es
b 2 – 4ac=(6) 2 – 4*1*11 = 36-44 = -8
Según la fórmula Shridharacharaya
x = [-b±√(b 2 -4ac)]/2a = x = [-(6) ± √(-8)]/2
x1 = [-( 6 ) + √(-8)]/2 = [-6 + √8i]/2 = 2[-3 + √2i]/2 = -3 + √2i
x2 = [-(6) – √(-8)]/2 = [-6 – √8i]/2 = 2[-3 – √2i]/2 = -3 – √2i
Por lo tanto, las raíces son 3,2. Ambos son imaginarios y conjugados entre sí (en pareja).
Gráficas para Raíces
El valor máximo/mínimo de la función cuadrática se encuentra en x = -b/2a
Prueba:
Obtenemos máximos o mínimos cuando d(f(x))/dx = 0.
Al diferenciar la función cuadrática f(x) = ax 2 + bx + c.
Obtenemos,
2ax + b = 0
x = -b/2a
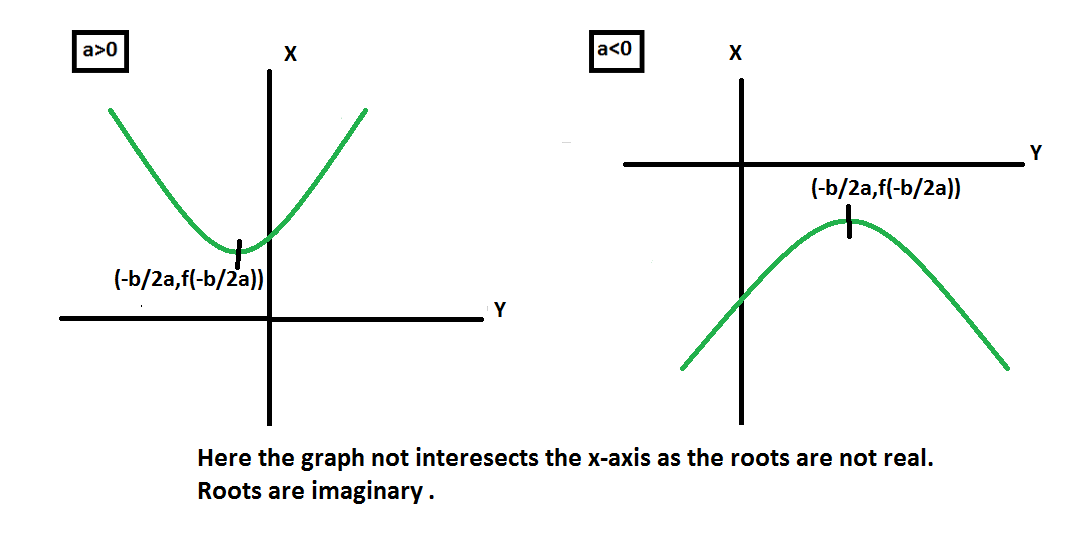
Esta x es máxima(a<0) o mínima(a>0).
1. Cuando b 2 – 4ac > 0

2. Cuando b 2 – 4ac = 0

3. Cuando b 2 – 4ac < 0
Problemas verbales de ecuaciones cuadráticas
Pregunta 1. La altura de un triángulo es menos de 4 cm que la base. El área del triángulo es de 30 cm 2 . Encuentra la altura y la base del triángulo.
Solución:
Sea la base del triangulo x cm entonces la altura es x-4 cm
Área del triángulo = 1/2*altura*base = 1/2*(x)(x – 4)=30
Área = x2 – 4x = 30* 2
= x2 – 4x = 60
= x 2 – 4x – 60 = 0
Discriminante = (-4) 2 – 4(1)(-60) = 16+240 = 256
x = [-b±√(b 2 – 4ac)]/2a = [-(-4)±√256]/2 = (4±16)/2
x = 20/2 o -12/2
x = 10 o -6
Como el lado no puede ser negativo, -6 no es correcto.
Entonces, cuando x es 10, base = 10 cm y altura = x – 4 = 10 – 4 = 6 cm
Por lo tanto, x = 10 es la respuesta válida y la base y la altura del triángulo son 10 y 6 respectivamente.
Pregunta 2. El volumen de una caja es de 600 pulgadas 2 . El largo de la caja es 2 pulgadas menos que el ancho. La altura de la caja es de 5 pulgadas. Encuentre las dimensiones de la caja.
Solución:
Deje que el ancho de la caja sea x pulgadas y luego la longitud = x – 2 pulgadas.
Volumen de la caja =Largo* Ancho *Alto = (x-2)(x)5= 600
x2 – 2x = 120 => x2 – 2x -120 = 0
x2 + 10x – 12x – 120 = 0
x(x+10) – 12(x+10)=0
(x – 12)(x + 10)=0
x = 12 o x = -10
Como el ancho no puede ser negativo, -10 no es correcto.
Cuando x = 12, ancho = 12 pulgadas, largo = x – 2 = 12 – 2 = 10 pulgadas, altura = 5 pulgadas
Pregunta 3. Se lanza una pelota desde lo alto de un edificio. su altura en metros sobre el suelo en función del tiempo está dada por h(t) = -4t 2 + 24t + 3. a) Cuanto tiempo tarda en alcanzar la altura máxima y cual es la altura máxima. b) Encuentre también el tiempo en que la pelota toca el suelo.
Solución:
a) Dado que a<0, entonces el tiempo para alcanzar la altura máxima es = -b/2a. (consulte la parte del gráfico)
t = -24/(2(-4)) = -24/-8
t = 3 seg.
Altura = h(t) = -4(3) 2 +24(3)+3 = 39 metros.
b) Cuando la pelota toca el suelo h(t)=0.
-4t 2 + 24t + 3 = 0
El discriminante de la ecuación dada es
b 2 – 4ac=(24) 2 – 4*(-4)*3 = 576 + 48 = 624
Según la fórmula Shridharacharaya
x = [-b±√(b 2 -4ac)]/2a = x = [-(24) ± √624]/[(2)(-4)]
x 1 = [-24 + √624]/-8= 4 [-6 + √39]/-8 = [-6 + √39]/-2 = [6 – √39]/2 = -0,122499 = – 0,1225 (aprox.)
x 2 = [-24 – √624]/-8= 4 [-6 – √39]/-8 = [-6 – √39]/-2 = [6 + √39]/2 = 6,122499 = 6,1225( aproximadamente)
Como el tiempo no puede ser negativo, [6 – √39]/2 seg no es correcto.
Por lo tanto, la pelota toca el suelo en [6 + √39]/2 = 6.122499 = 6.1225 seg.
Publicación traducida automáticamente
Artículo escrito por gunjeetajain910 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA