Introducción:
El reconocimiento de dígitos escritos a mano utilizando el conjunto de datos MNIST es un proyecto importante realizado con la ayuda de Neural Network. Básicamente detecta las imágenes escaneadas de dígitos escritos a mano.
Hemos llevado esto un paso más allá donde nuestro sistema de reconocimiento de dígitos escritos a mano no solo detecta imágenes escaneadas de dígitos escritos a mano, sino que también permite escribir dígitos en la pantalla con la ayuda de una GUI integrada para el reconocimiento.
Acercarse:
Abordaremos este proyecto utilizando una red neuronal de tres capas.
- La capa de entrada: Distribuye las características de nuestros ejemplos a la siguiente capa para el cálculo de activaciones de la siguiente capa.
- La capa oculta: Están formadas por unidades ocultas llamadas activaciones que proporcionan lazos no lineales para la red. Un número de capas ocultas puede variar según nuestros requisitos.
- La capa de salida: Los Nodes aquí se denominan unidades de salida. Nos proporciona la predicción final de la Red Neuronal sobre la base de la cual se pueden hacer las predicciones finales.
Una red neuronal es un modelo inspirado en el funcionamiento del cerebro. Consiste en múltiples capas que tienen muchas activaciones, esta activación se asemeja a las neuronas de nuestro cerebro. Una red neuronal intenta aprender un conjunto de parámetros en un conjunto de datos que podrían ayudar a reconocer las relaciones subyacentes. Las redes neuronales pueden adaptarse a los cambios de entrada; por lo que la red genera el mejor resultado posible sin necesidad de rediseñar los criterios de salida.
Metodología:
Hemos implementado una Red Neuronal con 1 capa oculta que tiene 100 unidades de activación (excluyendo las unidades de polarización). Los datos se cargan desde un archivo .mat , se extrajeron las características (X) y las etiquetas (y). Luego, las características se dividen por 255 para volver a escalarlas en un rango de [0,1] para evitar el desbordamiento durante el cálculo. Los datos se dividen en 60 000 ejemplos de entrenamiento y 10 000 de prueba. Feedforward se realiza con el conjunto de entrenamiento para calcular la hipótesis y luego se realiza backpropagation para reducir el error entre las capas. El parámetro de regularización lambda se establece en 0,1 para abordar el problema del sobreajuste. Optimizer se ejecuta durante 70 iteraciones para encontrar el modelo que mejor se ajuste.
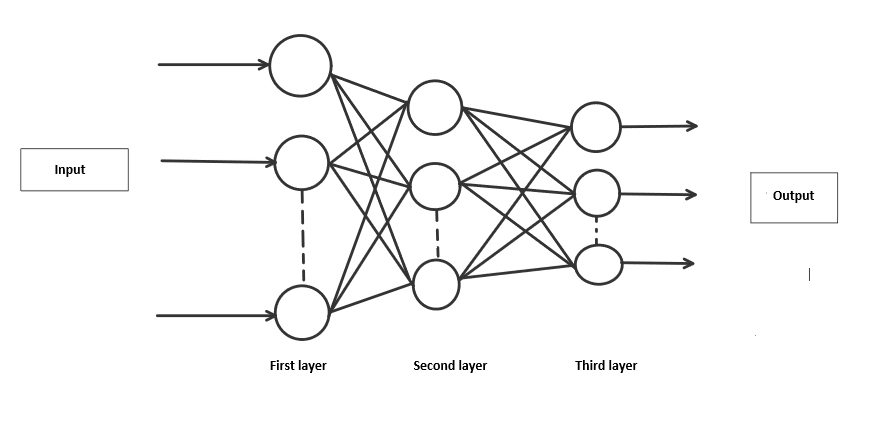
Capas de red neuronal
Nota:
- Guarde todos los archivos .py en el mismo directorio.
- Descargue el conjunto de datos de https://www.kaggle.com/avnishnish/mnist-original/download
Principal.py
Importando todas las bibliotecas requeridas, extraiga los datos del archivo mnist-original.mat . Luego, las características y las etiquetas se separarán de los datos extraídos. Después de eso, los datos se dividirán en ejemplos de entrenamiento (60 000) y de prueba (10 000). Inicialice aleatoriamente Thetas en el rango de [-0.15, +0.15] para romper la simetría y obtener mejores resultados. Además, se llama al optimizador para el entrenamiento de pesos, para minimizar la función de costo para predicciones apropiadas. Hemos utilizado el optimizador » minimizar » de la biblioteca » scipy.optimize » con el método » L-BFGS-B «. Hemos calculado la prueba, la «exactitud y precisión del conjunto de entrenamiento usando la función «predecir».
Python3
from scipy.io import loadmat
import numpy as np
from Model import neural_network
from RandInitialize import initialise
from Prediction import predict
from scipy.optimize import minimize
# Loading mat file
data = loadmat('mnist-original.mat')
# Extracting features from mat file
X = data['data']
X = X.transpose()
# Normalizing the data
X = X / 255
# Extracting labels from mat file
y = data['label']
y = y.flatten()
# Splitting data into training set with 60,000 examples
X_train = X[:60000, :]
y_train = y[:60000]
# Splitting data into testing set with 10,000 examples
X_test = X[60000:, :]
y_test = y[60000:]
m = X.shape[0]
input_layer_size = 784 # Images are of (28 X 28) px so there will be 784 features
hidden_layer_size = 100
num_labels = 10 # There are 10 classes [0, 9]
# Randomly initialising Thetas
initial_Theta1 = initialise(hidden_layer_size, input_layer_size)
initial_Theta2 = initialise(num_labels, hidden_layer_size)
# Unrolling parameters into a single column vector
initial_nn_params = np.concatenate((initial_Theta1.flatten(), initial_Theta2.flatten()))
maxiter = 100
lambda_reg = 0.1 # To avoid overfitting
myargs = (input_layer_size, hidden_layer_size, num_labels, X_train, y_train, lambda_reg)
# Calling minimize function to minimize cost function and to train weights
results = minimize(neural_network, x0=initial_nn_params, args=myargs,
options={'disp': True, 'maxiter': maxiter}, method="L-BFGS-B", jac=True)
nn_params = results["x"] # Trained Theta is extracted
# Weights are split back to Theta1, Theta2
Theta1 = np.reshape(nn_params[:hidden_layer_size * (input_layer_size + 1)], (
hidden_layer_size, input_layer_size + 1)) # shape = (100, 785)
Theta2 = np.reshape(nn_params[hidden_layer_size * (input_layer_size + 1):],
(num_labels, hidden_layer_size + 1)) # shape = (10, 101)
# Checking test set accuracy of our model
pred = predict(Theta1, Theta2, X_test)
print('Test Set Accuracy: {:f}'.format((np.mean(pred == y_test) * 100)))
# Checking train set accuracy of our model
pred = predict(Theta1, Theta2, X_train)
print('Training Set Accuracy: {:f}'.format((np.mean(pred == y_train) * 100)))
# Evaluating precision of our model
true_positive = 0
for i in range(len(pred)):
if pred[i] == y_train[i]:
true_positive += 1
false_positive = len(y_train) - true_positive
print('Precision =', true_positive/(true_positive + false_positive))
# Saving Thetas in .txt file
np.savetxt('Theta1.txt', Theta1, delimiter=' ')
np.savetxt('Theta2.txt', Theta2, delimiter=' ')
RandInicializar.py
Inicializa aleatoriamente theta entre un rango de [-epsilon, +epsilon].
Python3
import numpy as np def initialise(a, b): epsilon = 0.15 c = np.random.rand(a, b + 1) * ( # Randomly initialises values of thetas between [-epsilon, +epsilon] 2 * epsilon) - epsilon return c
Modelo.py
La función realiza feed-forward y backpropagation.
- Propagación directa: los datos de entrada se alimentan en la dirección directa a través de la red. Cada capa oculta acepta los datos de entrada, los procesa según la función de activación y los pasa a la capa sucesiva. Usaremos la función sigmoidea como nuestra «función de activación».
- Propagación hacia atrás: Es la práctica de afinar los pesos de una red neuronal en función de la tasa de error obtenida en la iteración anterior.
También calcula los costos de entropía cruzada para verificar los errores entre la predicción y los valores originales. Al final, se calcula el gradiente para el objetivo de optimización.
Python3
import numpy as np def neural_network(nn_params, input_layer_size, hidden_layer_size, num_labels, X, y, lamb): # Weights are split back to Theta1, Theta2 Theta1 = np.reshape(nn_params[:hidden_layer_size * (input_layer_size + 1)], (hidden_layer_size, input_layer_size + 1)) Theta2 = np.reshape(nn_params[hidden_layer_size * (input_layer_size + 1):], (num_labels, hidden_layer_size + 1)) # Forward propagation m = X.shape[0] one_matrix = np.ones((m, 1)) X = np.append(one_matrix, X, axis=1) # Adding bias unit to first layer a1 = X z2 = np.dot(X, Theta1.transpose()) a2 = 1 / (1 + np.exp(-z2)) # Activation for second layer one_matrix = np.ones((m, 1)) a2 = np.append(one_matrix, a2, axis=1) # Adding bias unit to hidden layer z3 = np.dot(a2, Theta2.transpose()) a3 = 1 / (1 + np.exp(-z3)) # Activation for third layer # Changing the y labels into vectors of boolean values. # For each label between 0 and 9, there will be a vector of length 10 # where the ith element will be 1 if the label equals i y_vect = np.zeros((m, 10)) for i in range(m): y_vect[i, int(y[i])] = 1 # Calculating cost function J = (1 / m) * (np.sum(np.sum(-y_vect * np.log(a3) - (1 - y_vect) * np.log(1 - a3)))) + (lamb / (2 * m)) * ( sum(sum(pow(Theta1[:, 1:], 2))) + sum(sum(pow(Theta2[:, 1:], 2)))) # backprop Delta3 = a3 - y_vect Delta2 = np.dot(Delta3, Theta2) * a2 * (1 - a2) Delta2 = Delta2[:, 1:] # gradient Theta1[:, 0] = 0 Theta1_grad = (1 / m) * np.dot(Delta2.transpose(), a1) + (lamb / m) * Theta1 Theta2[:, 0] = 0 Theta2_grad = (1 / m) * np.dot(Delta3.transpose(), a2) + (lamb / m) * Theta2 grad = np.concatenate((Theta1_grad.flatten(), Theta2_grad.flatten())) return J, grad
Predicción.py
Realiza la propagación hacia adelante para predecir el dígito.
Python3
import numpy as np def predict(Theta1, Theta2, X): m = X.shape[0] one_matrix = np.ones((m, 1)) X = np.append(one_matrix, X, axis=1) # Adding bias unit to first layer z2 = np.dot(X, Theta1.transpose()) a2 = 1 / (1 + np.exp(-z2)) # Activation for second layer one_matrix = np.ones((m, 1)) a2 = np.append(one_matrix, a2, axis=1) # Adding bias unit to hidden layer z3 = np.dot(a2, Theta2.transpose()) a3 = 1 / (1 + np.exp(-z3)) # Activation for third layer p = (np.argmax(a3, axis=1)) # Predicting the class on the basis of max value of hypothesis return p
GUI.py
Lanza una GUI para escribir dígitos. La imagen del dígito se almacena en el mismo directorio después de convertirla a escala de grises y reducir el tamaño a (28 X 28) píxeles.
Python3
from tkinter import *
import numpy as np
from PIL import ImageGrab
from Prediction import predict
window = Tk()
window.title("Handwritten digit recognition")
l1 = Label()
def MyProject():
global l1
widget = cv
# Setting co-ordinates of canvas
x = window.winfo_rootx() + widget.winfo_x()
y = window.winfo_rooty() + widget.winfo_y()
x1 = x + widget.winfo_width()
y1 = y + widget.winfo_height()
# Image is captured from canvas and is resized to (28 X 28) px
img = ImageGrab.grab().crop((x, y, x1, y1)).resize((28, 28))
# Converting rgb to grayscale image
img = img.convert('L')
# Extracting pixel matrix of image and converting it to a vector of (1, 784)
x = np.asarray(img)
vec = np.zeros((1, 784))
k = 0
for i in range(28):
for j in range(28):
vec[0][k] = x[i][j]
k += 1
# Loading Thetas
Theta1 = np.loadtxt('Theta1.txt')
Theta2 = np.loadtxt('Theta2.txt')
# Calling function for prediction
pred = predict(Theta1, Theta2, vec / 255)
# Displaying the result
l1 = Label(window, text="Digit = " + str(pred[0]), font=('Algerian', 20))
l1.place(x=230, y=420)
lastx, lasty = None, None
# Clears the canvas
def clear_widget():
global cv, l1
cv.delete("all")
l1.destroy()
# Activate canvas
def event_activation(event):
global lastx, lasty
cv.bind('<B1-Motion>', draw_lines)
lastx, lasty = event.x, event.y
# To draw on canvas
def draw_lines(event):
global lastx, lasty
x, y = event.x, event.y
cv.create_line((lastx, lasty, x, y), width=30, fill='white', capstyle=ROUND, smooth=TRUE, splinesteps=12)
lastx, lasty = x, y
# Label
L1 = Label(window, text="Handwritten Digit Recoginition", font=('Algerian', 25), fg="blue")
L1.place(x=35, y=10)
# Button to clear canvas
b1 = Button(window, text="1. Clear Canvas", font=('Algerian', 15), bg="orange", fg="black", command=clear_widget)
b1.place(x=120, y=370)
# Button to predict digit drawn on canvas
b2 = Button(window, text="2. Prediction", font=('Algerian', 15), bg="white", fg="red", command=MyProject)
b2.place(x=320, y=370)
# Setting properties of canvas
cv = Canvas(window, width=350, height=290, bg='black')
cv.place(x=120, y=70)
cv.bind('<Button-1>', event_activation)
window.geometry("600x500")
window.mainloop()
Resultado:
Precisión del conjunto de entrenamiento de 99.440000%
Exactitud del conjunto de prueba de 97.320000%
Precisión de 0.9944
Producción:
Este artículo es aportado por:
- Utkarsh Shaw ( https://auth.geeksforgeeks.org/user/utkarshshaw/profile )
- Tania ( https://auth.geeksforgeeks.org/user/taniachanana02/profile )
- Rishab Mamgai ( https://auth.geeksforgeeks.org/user/rishabmamgai/profile )
Publicación traducida automáticamente
Artículo escrito por utkarshshaw y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA