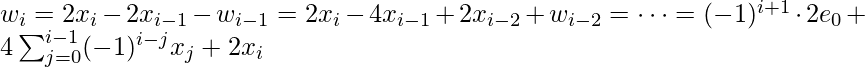Reconstrucción de histograma

En este artículo, discutiremos » Diagrama a histograma» , también conocido como «Búsqueda de intervalo» . Al tratar con datos estadísticos, los diagramas se representan con puntos únicos (o los números correspondientes) como las estrellas, que se supone que es un histograma con un cierto ancho, como se muestra en la figura a continuación.

Analizando el problema :

En el enunciado de este problema, la suposición es que todos los intervalos se mantienen juntos, es decir, no hay espacios ni superposiciones. El borde derecho de un contenedor es idéntico al borde izquierdo del siguiente contenedor. Dados N puntos , por lo tanto, N contenedores , la tarea es encontrar (N + 1) bordes de contenedores. Cada punto dado se encuentra en el centro exacto de su intervalo X. Esto da N ecuaciones para (N + 1) cantidades desconocidas, por lo que el sistema está indeterminado. Hay dos sugerencias:

Los contenedores serán lo más uniformes. Matemáticamente, se minimizará la variación de los anchos de sus bins.
Uno proporciona directamente un valor fijo para un borde de contenedor, solo los demás se derivan de eso.

Cálculos :

Aquí hay algunas suposiciones:

Sean x _i las coordenadas del punto (sus valores y son completamente irrelevantes para nosotros).
w _i los respectivos anchos de bin.
e _i las coordenadas de los bordes del bin.
Suponga que el x _i está ordenado en orden ascendente.

A continuación se muestra la imagen para ilustrar los conceptos anteriores:

Relation between considered quantities

De la representación anterior, dos relaciones simples que se pueden verificar fácilmente son:

$x_{i + 1} - x_i = \frac12(w_{i + 1} + w_i)$

$x_i = \frac12(e_i + e_{i + 1})$

La fórmula anterior simplifica los cálculos especialmente para N pares y es la razón por la que se obtienen resultados diferentes para valores pares e impares de N . Este último es directamente la fórmula de recurrencia que debe completar la array e[] (los puntos en el eje X del histograma).

¿Cómo minimizar la Varianza ?

La idea es similar a todos los problemas de minimización, es decir, verificar la derivada 0 . El problema es reducir su fórmula a una sola variable desconocida con la que luego podemos trabajar para encontrar el valor mínimo.

La varianza viene dada por:

$V=\frac1n\sum_{i=0}^{n-1}(w_i-\bar{w})^2=\frac1n\sum_{i=0}^{n-1}w_i^2-\bar{w}^2$

El valor del valor medio en la fórmula anterior viene dado por:

$\bar{w}=\frac1n\sum_{i=0}^{n-1}w_i=\frac1n(e_n-e_0)$

Derive la ecuación anterior con respecto a una cantidad arbitraria z como:

$\frac{dV}{dz}=\frac2n\sum_{i=0}^{n-1}w_i\frac{dw_i}{dz}-\frac2n\bar{w}\sum_{i=0}^{n-1}\frac{dw_i}{dz}$

Aplicando iterativamente la primera ecuación derivada arriba reemplazando w _i con (z = e ₀ ) . Por ejemplo:

$w_i=2x_i-2x_{i-1}-w_{i-1}=2x_i-4x_{i-1}+2x_{i-2}+w_{i-2}=\dots=(-1)^{i+1}\cdot2e_0+4\sum_{j=0}^{i-1}(-1)^{i-j}x_j+2x_i$

Poniendo todos los valores anteriores obtenidos para encontrar el valor de e ₀ :

Cuando N es impar, entonces

$e_0=\frac1{n^2-1}\sum_{i=0}^{n-1}(-1)^ix_i(2n^2-2in-n-1)$

Cuando N es par, entonces

$e_0=\frac1n\sum_{i=0}^{n-1}(-1)^ix_i(2n-2i-1)$

Alternativamente, usando el valor de z = e _N , da una fórmula más simple como:

Cuando N es impar, entonces

$e_N = \frac1{N^2-1}\sum_{i=0}^{n-1}(-1)^ix_i(2iN + N - 1)$

Cuando N es par, entonces

$e_N = \frac1n\sum_{i = 0}^{N - 1}(-1)^ix_i(2i + 1)$

Enfoque: La idea para resolver el problema dado es iterar dos bucles anidados, uno para encontrar el valor de e ₀ o e _N de acuerdo con la fórmula derivada y otro bucle para encontrar los elementos de la array e[] . Por tanto, la complejidad temporal será O(N) para todas las variantes. Ambos bucles funcionan recursivamente y el segundo bucle encuentra los elementos del arreglo e[] del anterior de acuerdo con la segunda ecuación dada arriba.

Nota:

El efecto de redondeo de las divisiones enteras se usa para manejar los casos de valores pares e impares de N .
Las funciones de C también funcionarán en C++ si se omite el registro de palabras clave en la siguiente implementación.
El programa requerirá un compilador de C del estándar C99 y un compilador de C++ de C++14 respectivamente.

A continuación se muestra la implementación del enfoque anterior:

C

// C program for the above approach
#include <stdio.h>
#include <stdlib.h>
#define N 6
  
// Function to fill the array elements
// e[] from the end
double* pointsToIntervalsN(
    int n, const double* x,
    double* e)
{
    // Check for array overlap
    if (n < 2 || !x || e < x && e + n >= x)
        return NULL;
  
    // If e is a NULL pointer, then
    // allocate the array
    if (e
        || (e
            = (double*)malloc(
                (n + 1) * sizeof(double)))) {
  
        // Find the value of m on the
        // basis of odd or even value of N
        const int m = n & 1 ? n : 2;
        const int j = m * n;
        register double sum = 0.;
  
        // Count i and x downwards
        for (int i = m / 2; i < j; i += m) {
            sum = i * *x++ - sum;
        }
        sum /= j / 2;
  
        // Note: m/2 and j/2 above are
        // integer divisions!
        for (e[n] = sum; n--; e[n] = sum)
            sum = 2 * *--x - sum;
    }
  
    // Including e==NULL for the case
    // of malloc error
    return e;
}
  
// Function to fill the output array
// from the front
double* pointsToIntervals0(const int n,
                           const double* x,
                           double* e)
{
    // Check for overlaps
    if (n < 2 || !x || e >= x && e < x + n)
        return NULL;
  
    if (e
        || (e
            = (double*)malloc(
                (n + 1) * sizeof(double)))) {
  
        const int m = n & 1 ? n : 2;
        const int j = m * n;
        register double sum = 0.;
  
        // Count i down and x
        // from the front
        x += n;
  
        for (int i = m / 2; i < j;
             i += m) {
            sum = i * *--x - sum;
        }
  
        // Update the value of sum
        sum /= j / 2;
  
        *e = sum;
        for (int i = 0; i < n;
             e[++i] = sum)
            sum = 2 * x[i] - sum;
    }
  
    // Return the updated e
    return e;
}
  
// Function to find thefixed single
// e value from which all other e's
// are derived
double* pointsToIntervalsFix(const int n,
                             const double* x,
                             double e_base,
                             double* e)
{
    // Base Case
    if (n < 1 || !x)
        return NULL;
  
    int k = 0;
  
    // Perform Binary Search for e_base
    for (int l = n; l > 1; l /= 2)
        if (e_base > x[k + l / 2])
            k += (l + 1) / 2;
  
    // The e_base is either the left
    // or the right edge of the bin
    // around x[k]
    if (e_base > x[k])
        ++k;
  
    // Now it's the left.
  
    // Assume e is filled the left side
    // first, the right side of e can
    // overlap with x
    if (e + k >= x && e < x + n)
        return NULL;
  
    // If the right side is filled
    // first, so that the left side
    // of e can overlap with x
    if (e || (e = (double*)malloc(
                  (n + 1) * sizeof(double)))) {
        e[k] = e_base;
  
        // Fill in both sides of array
        // e[] starting from k
        for (int i = k; i--; e[i] = e_base)
            e_base = 2 * x[i] - e_base;
  
        for (e_base = e[k]; k < n;
             e[++k] = e_base)
            e_base = 2 * x[k] - e_base;
    }
  
    return e;
}
  
// Driver Code
int main()
{
    double e_orig[N + 1]
        = { 4, 37, 121, 200, 234, 300, 365 };
    double x[N], e_recN[N + 1], e_rec0[N + 1];
    double e_base = 235.4, e_fix[N + 1];
  
    // Make x the mean values of the
    // neighbouring e_orig values:
    for (int i = N; i--;
         x[i] = (e_orig[i + 1] + e_orig[i]) / 2)
        ;
  
    // Function Call
    pointsToIntervalsN(N, x, e_recN);
    pointsToIntervals0(N, x, e_rec0);
    pointsToIntervalsFix(N, x, e_base, e_fix);
  
    printf("Example for n = %d:", N);
    printf("\nx     ");
    for (int i = 0; i < N; ++i)
        printf("% .3f", x[i]);
  
    printf("\ne_orig ");
  
    for (int i = 0; i <= N; ++i)
        printf("% .3f", e_orig[i]);
  
    printf("\ne_recN ");
  
    for (int i = 0; i <= N; ++i)
        printf("% .3f", e_recN[i]);
  
    printf("\ne_rec0 ");
  
    for (int i = 0; i <= N; ++i)
        printf("% .3f", e_rec0[i]);
  
    printf("\ne_fix  ");
  
    for (int i = 0; i <= N; ++i)
        printf("% .3f", e_fix[i]);
  
    return 0;
}

Producción:

Example for n = 6:
x      20.500 79.000 160.500 217.000 267.000 332.500
e_orig  4.000 37.000 121.000 200.000 234.000 300.000 365.000
e_recN  3.583 37.417 120.583 200.417 233.583 300.417 364.583
e_rec0  3.583 37.417 120.583 200.417 233.583 300.417 364.583
e_fix   5.400 35.600 122.400 198.600 235.400 298.600 366.400

Advertencias y perspectivas :

Ambos métodos, es decir, la varianza mínima y el borde fijo, ocasionalmente fallan de tal manera que se obtienen uno o más intervalos de histograma con ancho negativo, es decir, hay algunos e _i > e _{(i + 1}₎ aparentemente no clasificados correctamente. Esto siempre sucede cuando se toma cualquier valor aleatorio de X como entrada.
Intente arreglar el contenedor con el ancho «más negativo» de todos, con la esperanza de que todos los demás también se vean razonables.
Esto nos lleva a las perspectivas porque los dos métodos ilustrados anteriormente no son, con mucho, las únicas posibilidades para formular una condición adicional. En lugar de anchos de contenedores “posiblemente iguales” , suponga una tendencia como un aumento lineal de w _i o un mínimo absoluto de todos los w _i .

Publicación traducida automáticamente

Artículo escrito por wscheinast y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C

Deja una respuesta Cancelar la respuesta