Dada una array 2D, imprima todos los elementos de la array dada en orden diagonal. Por ejemplo, considere la siguiente array de entrada de 5 X 4.
Ejemplo:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
La impresión diagonal de la array anterior es
1 5 2 9 6 3 13 10 7 4 17 14 11 8 18 15 12 19 16 20
Otro ejemplo :
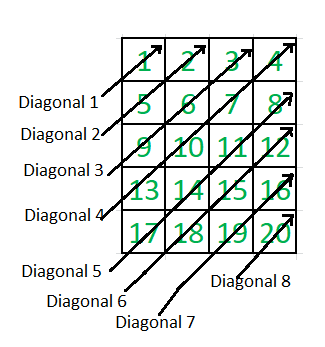
Le recomendamos encarecidamente que haga clic aquí y lo practique antes de pasar a la solución.
A continuación se muestra el código para la impresión en diagonal.
La impresión diagonal de una array dada «array [ROW] [COL]» siempre tiene «ROW + COL – 1» líneas en la salida.
Implementación:
C++
// C++ program to print all elements
// of given matrix in diagonal order
#include <bits/stdc++.h>
using namespace std;
#define ROW 5
#define COL 4
// A utility function to find min
// of two integers
int minu(int a, int b)
{
return (a < b) ? a : b;
}
// A utility function to find min
// of three integers
int min(int a, int b, int c)
{
return minu(minu(a, b), c);
}
// A utility function to find
// max of two integers
int max(int a, int b)
{
return (a > b) ? a : b;
}
// The main function that prints given
// matrix in diagonal order
void diagonalOrder(int matrix[][COL])
{
// There will be ROW+COL-1 lines
// in the output
for(int line = 1;
line <= (ROW + COL - 1);
line++)
{
/* Get column index of the first element
in this line of output.
The index is 0 for first ROW lines and
line - ROW for remaining lines */
int start_col = max(0, line - ROW);
/* Get count of elements in this line. The
count of elements is equal to minimum of
line number, COL-start_col and ROW */
int count = min(line, (COL - start_col), ROW);
/* Print elements of this line */
for(int j = 0; j < count; j++)
cout << setw(5) <<
matrix[minu(ROW, line) - j - 1][start_col + j];
/* Print elements of next
diagonal on next line */
cout << "\n";
}
}
// Utility function to print a matrix
void printMatrix(int matrix[ROW][COL])
{
for(int i = 0; i < ROW; i++)
{
for(int j = 0; j < COL; j++)
cout << setw(5) << matrix[i][j];
cout << "\n";
}
}
// Driver code
int main()
{
int M[ROW][COL] = { { 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 },
{ 13, 14, 15, 16 },
{ 17, 18, 19, 20 },};
cout << "Given matrix is " << endl;
printMatrix(M);
cout << "\nDiagonal printing of matrix is " << endl;
diagonalOrder(M);
return 0;
}
// This code is contributed by shubhamsingh10
C
// C program to print all elements
// of given matrix in diagonal order
#include <stdlib.h>
#define ROW 5
#define COL 4
// A utility function to find min of two integers
int minu(int a, int b)
{ return (a < b)? a: b; }
// A utility function to find min of three integers
int min(int a, int b, int c)
{ return minu(minu(a, b), c);}
// A utility function to find max of two integers
int max(int a, int b)
{ return (a > b)? a: b; }
// The main function that prints given matrix in
// diagonal order
void diagonalOrder(int matrix[][COL])
{
// There will be ROW+COL-1 lines in the output
for (int line=1; line<=(ROW + COL -1); line++)
{
/* Get column index of the first element
in this line of output.
The index is 0 for first ROW lines and
line - ROW for remaining lines */
int start_col = max(0, line-ROW);
/* Get count of elements in this line. The
count of elements is equal to minimum of
line number, COL-start_col and ROW */
int count = min(line, (COL-start_col), ROW);
/* Print elements of this line */
for (int j=0; j<count; j++)
printf("%5d ",
matrix[minu(ROW, line)-j-1][start_col+j]);
/* Print elements of next diagonal on next line */
printf("\n");
}
}
// Utility function to print a matrix
void printMatrix(int matrix[ROW][COL])
{
for (int i=0; i< ROW; i++)
{
for (int j=0; j<COL; j++)
printf("%5d ", matrix[i][j]);
printf("\n");
}
}
// Driver code
int main()
{
int M[ROW][COL] = {{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{13, 14, 15, 16},
{17, 18, 19, 20},
};
printf ("Given matrix is \n");
printMatrix(M);
printf ("\nDiagonal printing of matrix is \n");
diagonalOrder(M);
return 0;
}
Java
// Java program to print all elements
// of given matrix in diagonal order
class GFG {
static final int ROW = 5;
static final int COL = 4;
// A utility function to find min
// of two integers
static int min(int a, int b)
{
return (a < b) ? a : b;
}
// A utility function to find min
// of three integers
static int min(int a, int b, int c)
{
return min(min(a, b), c);
}
// A utility function to find max
// of two integers
static int max(int a, int b)
{
return (a > b) ? a : b;
}
// The main function that prints given
// matrix in diagonal order
static void diagonalOrder(int matrix[][])
{
// There will be ROW+COL-1 lines in the output
for (int line = 1;
line <= (ROW + COL - 1);
line++) {
// Get column index of the first
// element in this line of output.
// The index is 0 for first ROW
// lines and line - ROW for remaining lines
int start_col = max(0, line - ROW);
// Get count of elements in this line.
// The count of elements is equal to
// minimum of line number, COL-start_col and ROW
int count = min(line, (COL - start_col),
ROW);
// Print elements of this line
for (int j = 0; j < count; j++)
System.out.print(matrix[min(ROW, line)
- j- 1][start_col + j]
+ " ");
// Print elements of next diagonal on next line
System.out.println();
}
}
// Utility function to print a matrix
static void printMatrix(int matrix[][])
{
for (int i = 0; i < ROW; i++)
{
for (int j = 0; j < COL; j++)
System.out.print(matrix[i][j] + " ");
System.out.print("\n");
}
}
// Driver code
public static void main(String[] args)
{
int M[][] = {
{ 1, 2, 3, 4 }, { 5, 6, 7, 8 },
{ 9, 10, 11, 12 }, { 13, 14, 15, 16 },
{ 17, 18, 19, 20 },
};
System.out.print("Given matrix is \n");
printMatrix(M);
System.out.print(
"\nDiagonal printing of matrix is \n");
diagonalOrder(M);
}
}
// This code is contributed by Anant Agarwal.
Python3
# Python3 program to print all elements
# of given matrix in diagonal order
ROW = 5
COL = 4
# Main function that prints given
# matrix in diagonal order
def diagonalOrder(matrix):
# There will be ROW+COL-1 lines in the output
for line in range(1, (ROW + COL)):
# Get column index of the first element
# in this line of output. The index is 0
# for first ROW lines and line - ROW for
# remaining lines
start_col = max(0, line - ROW)
# Get count of elements in this line.
# The count of elements is equal to
# minimum of line number, COL-start_col and ROW
count = min(line, (COL - start_col), ROW)
# Print elements of this line
for j in range(0, count):
print(matrix[min(ROW, line) - j - 1]
[start_col + j], end="\t")
print()
# Utility function to print a matrix
def printMatrix(matrix):
for i in range(0, ROW):
for j in range(0, COL):
print(matrix[i][j], end="\t")
print()
# Driver Code
M = [[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16],
[17, 18, 19, 20]]
print("Given matrix is ")
printMatrix(M)
print("\nDiagonal printing of matrix is ")
diagonalOrder(M)
# This code is contributed by Nikita Tiwari.
C#
// C# program to print all elements
// of given matrix in diagonal order
using System;
using static System.Math;
class GFG {
static int ROW = 5;
static int COL = 4;
// The main function that prints given
// matrix in diagonal order
static void diagonalOrder(int[, ] matrix)
{
// There will be ROW+COL-1 lines in the output
for (int line = 1;
line <= (ROW + COL - 1);
line++) {
// Get column index of the first element
// in this line of output.The index is 0
// for first ROW lines and line - ROW for
// remaining lines
int start_col = Max(0, line - ROW);
// Get count of elements in this line. The
// count of elements is equal to minimum of
// line number, COL-start_col and ROW
int count = Min(line, Math.Min((COL - start_col), ROW));
// Print elements of this line
for (int j = 0; j < count; j++)
Console.Write(matrix[Min(ROW, line) - j - 1, start_col + j] + " ");
// Print elements of next diagonal
// on next line
Console.WriteLine();
}
}
// Utility function to print a matrix
static void printMatrix(int[, ] matrix)
{
for (int i = 0; i < ROW; i++)
{
for (int j = 0; j < COL; j++)
Console.Write(matrix[i, j] + " ");
Console.WriteLine("\n");
}
}
// Driver code
public static void Main()
{
int[, ] M = { { 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 },
{ 13, 14, 15, 16 },
{ 17, 18, 19, 20 } };
Console.Write("Given matrix is \n");
printMatrix(M);
Console.Write("\nDiagonal printing" + " of matrix is \n");
diagonalOrder(M);
}
}
// This code is contributed by Sam007.
PHP
<?php
// PHP Code for Zigzag (or diagonal)
// traversal of Matrix
$ROW = 5;
$COL = 4;
// The main function that prints
// given matrix in diagonal order
function diagonalOrder(&$matrix)
{
global $ROW, $COL;
// There will be ROW+COL-1
// lines in the output
for ($line = 1;
$line <= ($ROW + $COL - 1); $line++)
{
/* Get column index of the first
element in this line of output.
The index is 0 for first ROW lines
and line - ROW for remaining lines */
$start_col = max(0, $line - $ROW);
/* Get count of elements in this line.
The count of elements is equal to
minimum of line number, COL-start_col
and ROW */
$count = min($line, ($COL -
$start_col), $ROW);
/* Print elements of this line */
for ($j = 0; $j < $count; $j++)
{
echo $matrix[min($ROW, $line) -
$j - 1][$start_col + $j];
echo "\t";
}
/* Print elements of next
diagonal on next line */
print("\n");
}
}
// Utility function
// to print a matrix
function printMatrix(&$matrix)
{
global $ROW, $COL;
for ($i = 0; $i < $ROW; $i++)
{
for ($j = 0; $j < $COL; $j++)
{
echo $matrix[$i][$j] ;
echo "\t";
}
print("\n");
}
}
// Driver Code
$M = array(array(1, 2, 3, 4),
array(5, 6, 7, 8),
array(9, 10, 11, 12),
array(13, 14, 15, 16),
array(17, 18, 19, 20));
echo "Given matrix is \n";
printMatrix($M);
printf ("\nDiagonal printing " .
"of matrix is \n");
diagonalOrder($M);
// This code is contributed
// by ChitraNayal
?>
Javascript
<script>
// Javascript program to print all elements
// of given matrix in diagonal order
let ROW = 5;
let COL = 4;
// A utility function to find min
// of two integers
function min(a, b)
{
return (a < b) ? a : b;
}
// A utility function to find min
// of three integer
function _min(a, b, c)
{
return min(min(a, b), c);
}
// A utility function to find max
// of two integers
function max(a,b)
{
return (a > b) ? a : b;
}
// The main function that prints given
// matrix in diagonal order
function diagonalOrder(matrix)
{
// There will be ROW+COL-1 lines in the output
for (let line = 1;
line <= (ROW + COL - 1);
line++) {
// Get column index of the first
// element in this line of output.
// The index is 0 for first ROW
// lines and line - ROW for remaining lines
let start_col = max(0, line - ROW);
// Get count of elements in this line.
// The count of elements is equal to
// minimum of line number, COL-start_col and ROW
let count = min(line, (COL - start_col),
ROW);
// Print elements of this line
for (let j = 0; j < count; j++)
document.write(matrix[min(ROW, line)
- j- 1][start_col + j]
+ " ");
// Print elements of next diagonal on next line
document.write("<br>");
}
}
// Utility function to print a matrix
function printMatrix(matrix)
{
for (let i = 0; i < ROW; i++)
{
for (let j = 0; j < COL; j++)
document.write(matrix[i][j] + " ");
document.write("<br>");
}
}
// Driver code
let M = [[ 1, 2, 3, 4 ], [ 5, 6, 7, 8 ],
[ 9, 10, 11, 12 ], [ 13, 14, 15, 16 ],
[ 17, 18, 19, 20 ]];
document.write("Given matrix is <br>");
printMatrix(M);
document.write(
"<br>Diagonal printing of matrix is <br>");
diagonalOrder(M);
// This code is contributed by ab2127
</script>
Given matrix is
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
17 18 19 20
Diagonal printing of matrix is
1
5 2
9 6 3
13 10 7 4
17 14 11 8
18 15 12
19 16
20
Complejidad temporal: O(fila x columna)
Espacio auxiliar: O(1)
A continuación se muestra un método alternativo para resolver el problema anterior.
Matrix => 1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
17 18 19 20
Observe the sequence
1 / 2 / 3 / 4
/ 5 / 6 / 7 / 8
/ 9 / 10 / 11 / 12
/ 13 / 14 / 15 / 16
/ 17 / 18 / 19 / 20
Implementación:
C++
#include <bits/stdc++.h>
#define R 5
#define C 4
using namespace std;
bool isValid(int i, int j)
{
if (i < 0 || i >= R
|| j >= C || j < 0)
return false;
return true;
}
void diagonalOrder(int arr[][C])
{
/* through this for loop we choose
each element of first column as
starting point and print diagonal
starting at it.
arr[0][0], arr[1][0]....arr[R-1][0]
are all starting points */
for (int k = 0; k < R; k++)
{
cout << arr[k][0] << " ";
// set row index for next point in
// diagonal
int i = k - 1;
// set column index for next point in
// diagonal
int j = 1;
/* Print Diagonally upward */
while (isValid(i, j)) {
cout << arr[i][j] << " ";
i--;
// move in upright direction
j++;
}
cout << endl;
}
/* through this for loop we choose
each element of last row as starting
point (except the [0][c-1] it has
already been processed in previous
for loop) and print diagonal starting
at it. arr[R-1][0], arr[R-1][1]....arr[R-1][c-1]
are all starting points
*/
// Note : we start from k = 1 to C-1;
for (int k = 1; k < C; k++)
{
cout << arr[R - 1][k] << " ";
// set row index for next point in
// diagonal
int i = R - 2;
// set column index for next point in
// diagonal
int j = k + 1;
/* Print Diagonally upward */
while (isValid(i, j))
{
cout << arr[i][j] << " ";
i--;
// move in upright direction
j++;
}
cout << endl;
}
}
// Driver Code
int main()
{
int arr[][C] = {
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 },
{ 13, 14, 15, 16 },
{ 17, 18, 19, 20 },
};
diagonalOrder(arr);
return 0;
}
Java
// JAVA Code for Zigzag (or diagonal)
// traversal of Matrix
class GFG {
public static int R, C;
private static void diagonalOrder(int[][] arr)
{
/* through this for loop we choose each
element of first column as starting point
and print diagonal starting at it. arr[0][0],
arr[1][0]....arr[R-1][0] are all starting points */
for (int k = 0; k < R; k++) {
System.out.print(arr[k][0] + " ");
// set row index for next
// point in diagonal
int i = k - 1;
// set column index for
// next point in diagonal
int j = 1;
/* Print Diagonally upward */
while (isValid(i, j))
{
System.out.print(arr[i][j] + " ");
i--;
// move in upright direction
j++;
}
System.out.println("");
}
/* through this for loop we choose each element
of last row as starting point (except the
[0][c-1] it has already been processed in
previous for loop) and print diagonal
starting at it. arr[R-1][0], arr[R-1][1]....
arr[R-1][c-1] are all starting points */
// Note : we start from k = 1 to C-1;
for (int k = 1; k < C; k++) {
System.out.print(arr[R - 1][k] + " ");
// set row index for next
// point in diagonal
int i = R - 2;
// set column index for
// next point in diagonal
int j = k + 1;
/* Print Diagonally upward */
while (isValid(i, j))
{
System.out.print(arr[i][j] + " ");
// move in upright direction
i--;
j++;
}
System.out.println("");
}
}
public static boolean isValid(int i, int j)
{
if (i < 0 || i >= R
|| j >= C || j < 0)
return false;
return true;
}
// Driver code
public static void main(String[] args)
{
int arr[][] = {
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 },
{ 13, 14, 15, 16 },
{ 17, 18, 19, 20 },
};
R = arr.length;
C = arr[0].length;
// Function call
diagonalOrder(arr);
}
}
// This code is contributed by Arnav Kr. Mandal.
Python3
# Python3 program to print all elements # of given matrix in diagonal order R = 5 C = 4 def isValid(i, j): if (i < 0 or i >= R or j >= C or j < 0): return False return True def diagonalOrder(arr): # through this for loop we choose each element # of first column as starting point and print # diagonal starting at it. # arr[0][0], arr[1][0]....arr[R-1][0] # are all starting points for k in range(0, R): print(arr[k][0], end=" ") # set row index for next point in diagonal i = k - 1 # set column index for next point in diagonal j = 1 # Print Diagonally upward while (isValid(i, j)): print(arr[i][j], end=" ") i -= 1 j += 1 # move in upright direction print() # Through this for loop we choose each # element of last row as starting point # (except the [0][c-1] it has already been # processed in previous for loop) and print # diagonal starting at it. # arr[R-1][0], arr[R-1][1]....arr[R-1][c-1] # are all starting points # Note : we start from k = 1 to C-1; for k in range(1, C): print(arr[R-1][k], end=" ") # set row index for next point in diagonal i = R - 2 # set column index for next point in diagonal j = k + 1 # Print Diagonally upward while (isValid(i, j)): print(arr[i][j], end=" ") i -= 1 j += 1 # move in upright direction print() # Driver Code arr = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16], [17, 18, 19, 20]] # Function call diagonalOrder(arr) # This code is contributed by Nikita Tiwari.
C#
// C# Code for Zigzag (or diagonal)
// traversal of Matrix
using System;
class GFG {
public static int R, C;
private static void diagonalOrder(int[, ] arr)
{
/* through this for loop we
choose each element of first
column as starting point and
print diagonal starting at it.
arr[0,0], arr[1,0]....arr[R-1,0]
are all starting points */
for (int k = 0; k < R; k++)
{
Console.Write(arr[k, 0] + " ");
// set row index for next
// point in diagonal
int i = k - 1;
// set column index for
// next point in diagonal
int j = 1;
/* Print Diagonally upward */
while (isValid(i, j))
{
Console.Write(arr[i, j] + " ");
i--;
// move in upright direction
j++;
}
Console.Write("\n");
}
/* through this for loop we
choose each element of last
row as starting point (except
the [0][c-1] it has already
been processed in previous for
loop) and print diagonal starting
at it. arr[R-1,0], arr[R-1,1]....
arr[R-1,c-1] are all starting points */
// Note : we start from k = 1 to C-1;
for (int k = 1; k < C; k++)
{
Console.Write(arr[R - 1, k] + " ");
// set row index for next
// point in diagonal
int i = R - 2;
// set column index for
// next point in diagonal
int j = k + 1;
/* Print Diagonally upward */
while (isValid(i, j))
{
Console.Write(arr[i, j] + " ");
i--;
j++; // move in upright direction
}
Console.Write("\n");
}
}
public static bool isValid(int i, int j)
{
if (i < 0 || i >= R || j >= C || j < 0)
return false;
return true;
}
// Driver code
public static void Main()
{
int[, ] arr = { { 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 },
{ 13, 14, 15, 16 },
{ 17, 18, 19, 20 } };
R = arr.GetLength(0);
C = arr.GetLength(1);
// Function call
diagonalOrder(arr);
}
}
// This code is contributed
// by ChitraNayal
PHP
<?php
// PHP code for Zigzag (or diagonal)
// traversal of Matrix
define("R", 5);
define("C", 4);
function isValid($i, $j)
{
if ($i < 0 || $i >= R ||
$j >= C || $j < 0) return false;
return true;
}
function diagonalOrder(&$arr)
{
/* through this for loop we choose
each element of first column as
starting point and print diagonal
starting at it.
arr[0][0], arr[1][0]....arr[R-1][0]
are all starting points */
for ($k = 0; $k < R; $k++)
{
echo $arr[$k][0] . " ";
$i = $k - 1; // set row index for next
// point in diagonal
$j = 1; // set column index for next
// point in diagonal
/* Print Diagonally upward */
while (isValid($i,$j))
{
echo $arr[$i][$j] . " ";
$i--;
$j++; // move in upright direction
}
echo "\n";
}
/* through this for loop we choose each
element of last row as starting point
(except the [0][c-1] it has already been
processed in previous for loop) and print
diagonal starting at it. arr[R-1][0],
arr[R-1][1]....arr[R-1][c-1] are all
starting points */
//Note : we start from k = 1 to C-1;
for ($k = 1; $k < C; $k++)
{
echo $arr[R - 1][$k] . " ";
$i = R - 2; // set row index for next
// point in diagonal
$j = $k + 1; // set column index for next
// point in diagonal
/* Print Diagonally upward */
while (isValid($i, $j))
{
echo $arr[$i][$j] . " ";
$i--;
$j++; // move in upright direction
}
echo "\n";
}
}
// Driver Code
$arr = array(array(1, 2, 3, 4),
array(5, 6, 7, 8),
array(9, 10, 11, 12),
array(13, 14, 15, 16),
array(17, 18, 19, 20));
// Function call
diagonalOrder($arr);
// This code is contributed
// by rathbhupendra
?>
Javascript
<script>
// JAVA Code for Zigzag (or diagonal)
// traversal of Matrix
var R, C;
function diagonalOrder( arr)
{
/* through this for loop we choose each
element of first column as starting point
and print diagonal starting at it. arr[0][0],
arr[1][0]....arr[R-1][0] are all starting points */
for (var k = 0; k < R; k++) {
document.write(arr[k][0] + " ");
// set row index for next
// point in diagonal
var i = k - 1;
// set column index for
// next point in diagonal
var j = 1;
/* Print Diagonally upward */
while (isValid(i, j))
{
document.write(arr[i][j] + " ");
i--;
// move in upright direction
j++;
}
document.writeln("<br>");
}
/* through this for loop we choose each element
of last row as starting point (except the
[0][c-1] it has already been processed in
previous for loop) and print diagonal
starting at it. arr[R-1][0], arr[R-1][1]....
arr[R-1][c-1] are all starting points */
// Note : we start from k = 1 to C-1;
for (var k = 1; k < C; k++) {
document.write(arr[R - 1][k] + " ");
// set row index for next
// point in diagonal
var i = R - 2;
// set column index for
// next point in diagonal
var j = k + 1;
/* Print Diagonally upward */
while (isValid(i, j))
{
document.write(arr[i][j] + " ");
// move in upright direction
i--;
j++;
}
document.writeln("<br>");
}
}
function isValid( i, j)
{
if (i < 0 || i >= R
|| j >= C || j < 0)
return false;
return true;
}
// Driver code
var arr = [
[ 1, 2, 3, 4 ],
[ 5, 6, 7, 8 ],
[ 9, 10, 11, 12 ],
[ 13, 14, 15, 16 ],
[ 17, 18, 19, 20 ],
];
R = arr.length;
C = arr[0].length;
// Function call
diagonalOrder(arr);
// This code is contributed by shivanisinghss2110
</script>
1 5 2 9 6 3 13 10 7 4 17 14 11 8 18 15 12 19 16 20
Complejidad temporal: O(fila x columna)
Espacio auxiliar: O(1)
Gracias a Gaurav Ahirwar por sugerir este método.
- Imprimir array en forma antiespiral
- Array de impresión en forma de espiral
- Imprimir una array dada en forma de zigzag
Este artículo fue compilado por Ashish Anand y revisado por el equipo de GeeksforGeeks. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Otro enfoque:
Es una observación aguda que la suma de [i+j], que son los índices de la array, permanece igual en toda la diagonal. Así que explotaremos esta propiedad de la array para que nuestro código sea corto y simple.

A continuación se muestra la implementación de la idea anterior:
C++
#include <bits/stdc++.h>
#define R 5
#define C 4
using namespace std;
void diagonalOrder(int arr[][C],
int n, int m)
{
// we will use a 2D vector to
// store the diagonals of our array
// the 2D vector will have (n+m-1)
// rows that is equal to the number of
// diagonals
vector<vector<int> > ans(n + m - 1);
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
ans[i + j].push_back(arr[j][i]);
}
}
for (int i = 0; i < ans.size(); i++)
{
for (int j = 0; j < ans[i].size(); j++)
cout << ans[i][j] << " ";
cout << endl;
}
}
// Driver Code
int main()
{
// we have a matrix of n rows
// and m columns
int n = 5, m = 4;
int arr[][C] = {
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 },
{ 13, 14, 15, 16 },
{ 17, 18, 19, 20 },
};
// Function call
diagonalOrder(arr, n, m);
return 0;
}
Java
import java.util.*;
import java.io.*;
class GFG
{
public static int R = 5, C = 4;
public static void diagonalOrder(int[][] arr, int n, int m)
{
// we will use a 2D vector to
// store the diagonals of our array
// the 2D vector will have (n+m-1)
// rows that is equal to the number of
// diagonals
ArrayList<ArrayList<Integer>> ans = new ArrayList<ArrayList<Integer>>(n+m-1);
for(int i = 0; i < n + m - 1; i++)
{
ans.add(new ArrayList<Integer>());
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
(ans.get(i+j)).add(arr[i][j]);
}
}
for (int i = 0; i < ans.size(); i++)
{
for (int j = ans.get(i).size() - 1; j >= 0; j--)
{ System.out.print(ans.get(i).get(j)+ " ");
}
System.out.println();
}
}
// Driver code
public static void main (String[] args) {
int n = 5, m = 4;
int[][] arr={
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 },
{ 13, 14, 15, 16 },
{ 17, 18, 19, 20 },
};
// Function call
diagonalOrder(arr, n, m);
}
}
// This code is contributed by Manu Pathria
Python3
R = 5 C = 5 def diagonalOrder(arr, n, m): # we will use a 2D vector to # store the diagonals of our array # the 2D vector will have (n+m-1) # rows that is equal to the number of # diagonals ans = [[] for i in range(n + m - 1)] for i in range(m): for j in range(n): ans[i + j].append(arr[j][i]) for i in range(len(ans)): for j in range(len(ans[i])): print(ans[i][j], end = " ") print() # Driver Code # we have a matrix of n rows # and m columns n = 5 m = 4 # Function call arr = [[1, 2, 3, 4],[ 5, 6, 7, 8],[9, 10, 11, 12 ],[13, 14, 15, 16 ],[ 17, 18, 19, 20]] diagonalOrder(arr, n, m) # This code is contributed by rag2127
C#
using System;
using System.Collections.Generic;
public class GFG
{
public static int R = 5, C = 4;
public static void diagonalOrder(int[,] arr, int n, int m)
{
// we will use a 2D vector to
// store the diagonals of our array
// the 2D vector will have (n+m-1)
// rows that is equal to the number of
// diagonals
List<List<int>> ans = new List<List<int>>(n+m-1);
for(int i = 0; i < n + m - 1; i++)
{
ans.Add(new List<int>());
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
(ans[i + j]).Add(arr[i, j]);
}
}
for (int i = 0; i < ans.Count; i++)
{
for (int j = ans[i].Count - 1; j >= 0; j--)
{
Console.Write(ans[i][j] + " ");
}
Console.WriteLine();
}
}
// Driver code
static public void Main ()
{
int n = 5, m = 4;
int[,] arr={
{ 1, 2, 3, 4 },
{ 5, 6, 7, 8 },
{ 9, 10, 11, 12 },
{ 13, 14, 15, 16 },
{ 17, 18, 19, 20 },
};
// Function call
diagonalOrder(arr, n, m);
}
}
// This code is contributed by avanitrachhadiya2155
Javascript
<script>
var R = 5;
var C = 4;
function diagonalOrder(arr, n, m)
{
// we will use a 2D vector to
// store the diagonals of our array
// the 2D vector will have (n+m-1)
// rows that is equal to the number of
// diagonals
var ans = Array.from(Array(n+m-1), ()=>Array());
for (var i = 0; i < n; i++)
{
for (var j = 0; j < m; j++)
{
ans[i + j].push(arr[i][j]);
}
}
for (var i = 0; i < ans.length; i++)
{
for (var j = ans[i].length - 1; j >= 0; j--)
{
document.write(ans[i][j] + " ");
}
document.write("<br>");
}
}
// Driver Code
// we have a matrix of n rows
// and m columns
var n = 5, m = 4;
var arr = [
[ 1, 2, 3, 4 ],
[ 5, 6, 7, 8 ],
[ 9, 10, 11, 12 ],
[ 13, 14, 15, 16 ],
[ 17, 18, 19, 20 ],
];
// Function call
diagonalOrder(arr, n, m);
// This code is contributed by rrrtnx.
</script>
1 5 2 9 6 3 13 10 7 4 17 14 11 8 18 15 12 19 16 20
Complejidad de Tiempo: O(fila x columna)
Espacio Auxiliar: O(fila + columna)
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA