Recorte de línea | Conjunto 2 (algoritmo de Cyrus Beck)

Antecedentes :
Cyrus Beck es un algoritmo de recorte de línea creado para polígonos convexos. Permite el recorte de línea para ventanas no rectangulares, a diferencia de Cohen Sutherland o Nicholl Le Nicholl . También elimina el recorte repetido necesario en Cohen Sutherland .

Input: 
 1. Convex area of interest 
    which is defined by a set of coordinates
    given in a clockwise fashion.
 2. vertices which are an array of coordinates: 
    consisting of pairs (x, y)
 3. n which is the number of vertices
 4. A line to be clipped 
    given by a set of coordinates.
 5. line which is an array of coordinates: 
    consisting of two pairs, (x0, y0) and (x1, y1)
Output:
 1. Coordinates of line clipping which is the Accepted clipping
 2. Coordinates (-1, -1) which is the Rejected clipping

Algoritmo:

Se calculan las normales de cada arista.
Se calcula el vector para la línea de recorte.
Se calcula el producto punto entre la diferencia de un vértice por arista y un punto final seleccionado de la línea de recorte y la normal de la arista (para todas las aristas).
Se calcula el producto punto entre el vector de la línea de recorte y la normal del borde (para todos los bordes).
El primer producto escalar se divide por el segundo producto escalar y se multiplica por -1. Esto es T’.
Los valores de ‘t’ se clasifican como entrantes o salientes (desde todos los bordes) observando sus denominadores (último producto escalar).
Se elige un valor de ‘t’ de cada grupo y se pone en la forma paramétrica de una línea para calcular las coordenadas.
Si el valor ‘t’ entrante es mayor que el valor ‘t’ saliente, se rechaza la línea de recorte.

Casos :

Caso 1: La línea está parcialmente dentro de la ventana de recorte:

0 < t_E < t_L < 1

where t_E is 't' value for entering intersection point
      t_L is 't' value for exiting intersection point

Caso 2: La línea tiene un punto dentro o ambos lados dentro de la ventana o los puntos de intersección están en los puntos finales de la línea :
```
0 ≤ t_E ≤ t_L ≤ 1
```
Caso 3: La línea está completamente fuera de la ventana:
```
t_L < t_E
```

Pseudocódigo:

Primero, calcule la forma paramétrica de la línea a recortar y luego siga el algoritmo.

Elija un punto llamado P ₁ de los dos puntos de la recta (P ₀ P ₁ ).

Ahora, para cada borde del polígono, calcule el punto normal que se aleja del centro del polígono, a saber, N ₁ , N ₂ , etc.

Ahora, para cada arista, elija P _Ei (i -> i ^-ésima arista) (elija cualquiera de los vértices de la arista correspondiente, por ejemplo: para el polígono ABCD, para el lado AB, P _Ei puede ser el punto A o el punto B) y calcule

P₀ - P_Ei

Luego calcula

P₁ - P₀

Luego calcule los siguientes productos escalares para cada borde:

N_i . (P₀ - P_Ei)
N_i . (P₁ - P₀) 

where i -> i^th edge of the convex polygon

Luego calcule los valores ‘t’ correspondientes para cada borde por:

    N_i . (P₀ - P_Ei)
t = ------------------
    -(N_i . (P₁ - P₀))

Luego agrupe los valores de ‘t’ para los cuales el N _i . (P ₁ – P ₀ ) resultó ser negativo y tome el mínimo de todos ellos y 1.

Del mismo modo club todos los valores ‘t’ para los que el N _i . (P ₁ – P ₀ ) resultó ser positivo y tomó el máximo de todos los valores ‘t’ aporreados y 0.

Ahora, los dos valores ‘t’ obtenidos de este algoritmo se insertan en la forma paramétrica de la línea ‘a recortar’ y los dos puntos resultantes obtenidos son los puntos recortados.

Implementación : aquí hay una implementación de los pasos anteriores en la biblioteca de gráficos SFML C++. También puede presionar cualquier tecla para quitar la línea y presionar cualquier tecla para cortar la línea.

// C++ Program to implement Cyrus Beck
  
#include <SFML/Graphics.hpp>
#include <iostream>
#include <utility>
#include <vector>
  
using namespace std;
using namespace sf;
  
// Function to draw a line in SFML
void drawline(RenderWindow* window, pair<int, int> p0, pair<int, int> p1)
{
    Vertex line[] = {
        Vertex(Vector2f(p0.first, p0.second)),
        Vertex(Vector2f(p1.first, p1.second))
    };
    window->draw(line, 2, Lines);
}
  
// Function to draw a polygon, given vertices
void drawPolygon(RenderWindow* window, pair<int, int> vertices[], int n)
{
    for (int i = 0; i < n - 1; i++)
        drawline(window, vertices[i], vertices[i + 1]);
    drawline(window, vertices[0], vertices[n - 1]);
}
  
// Function to take dot product
int dot(pair<int, int> p0, pair<int, int> p1)
{
    return p0.first * p1.first + p0.second * p1.second;
}
  
// Function to calculate the max from a vector of floats
float max(vector<float> t)
{
    float maximum = INT_MIN;
    for (int i = 0; i < t.size(); i++)
        if (t[i] > maximum)
            maximum = t[i];
    return maximum;
}
  
// Function to calculate the min from a vector of floats
float min(vector<float> t)
{
    float minimum = INT_MAX;
    for (int i = 0; i < t.size(); i++)
        if (t[i] < minimum)
            minimum = t[i];
    return minimum;
}
  
// Cyrus Beck function, returns a pair of values
// that are then displayed as a line
pair<int, int>* CyrusBeck(pair<int, int> vertices[],
                          pair<int, int> line[], int n)
{
  
    // Temporary holder value that will be returned
    pair<int, int>* newPair = new pair<int, int>[2];
  
    // Normals initialized dynamically(can do it statically also, doesn't matter)
    pair<int, int>* normal = new pair<int, int>[n];
  
    // Calculating the normals
    for (int i = 0; i < n; i++) {
        normal[i].second = vertices[(i + 1) % n].first - vertices[i].first;
        normal[i].first = vertices[i].second - vertices[(i + 1) % n].second;
    }
  
    // Calculating P1 - P0
    pair<int, int> P1_P0
        = make_pair(line[1].first - line[0].first,
                    line[1].second - line[0].second);
  
    // Initializing all values of P0 - PEi
    pair<int, int>* P0_PEi = new pair<int, int>[n];
  
    // Calculating the values of P0 - PEi for all edges
    for (int i = 0; i < n; i++) {
  
        // Calculating PEi - P0, so that the
        // denominator won't have to multiply by -1
        P0_PEi[i].first
            = vertices[i].first - line[0].first;
  
        // while calculating 't'
        P0_PEi[i].second = vertices[i].second - line[0].second;
    }
  
    int *numerator = new int[n], *denominator = new int[n];
  
    // Calculating the numerator and denominators
    // using the dot function
    for (int i = 0; i < n; i++) {
        numerator[i] = dot(normal[i], P0_PEi[i]);
        denominator[i] = dot(normal[i], P1_P0);
    }
  
    // Initializing the 't' values dynamically
    float* t = new float[n];
  
    // Making two vectors called 't entering'
    // and 't leaving' to group the 't's
    // according to their denominators
    vector<float> tE, tL;
  
    // Calculating 't' and grouping them accordingly
    for (int i = 0; i < n; i++) {
  
        t[i] = (float)(numerator[i]) / (float)(denominator[i]);
  
        if (denominator[i] > 0)
            tE.push_back(t[i]);
        else
            tL.push_back(t[i]);
    }
  
    // Initializing the final two values of 't'
    float temp[2];
  
    // Taking the max of all 'tE' and 0, so pushing 0
    tE.push_back(0.f);
    temp[0] = max(tE);
  
    // Taking the min of all 'tL' and 1, so pushing 1
    tL.push_back(1.f);
    temp[1] = min(tL);
  
    // Entering 't' value cannot be
    // greater than exiting 't' value,
    // hence, this is the case when the line
    // is completely outside
    if (temp[0] > temp[1]) {
        newPair[0] = make_pair(-1, -1);
        newPair[1] = make_pair(-1, -1);
        return newPair;
    }
  
    // Calculating the coordinates in terms of x and y
    newPair[0].firs
        t
        = (float)line[0].first
          + (float)P1_P0.first * (float)temp[0];
    newPair[0].second
        = (float)line[0].second
          + (float)P1_P0.second * (float)temp[0];
    newPair[1].first
        = (float)line[0].first
          + (float)P1_P0.first * (float)temp[1];
    newPair[1].second
        = (float)line[0].second
          + (float)P1_P0.second * (float)temp[1];
    cout << '(' << newPair[0].first << ", "
         << newPair[0].second << ") ("
         << newPair[1].first << ", "
         << newPair[1].second << ")";
  
    return newPair;
}
  
// Driver code
int main()
{
  
    // Setting up a window and loop
    // and the vertices of the polygon and line
    RenderWindow window(VideoMode(500, 500), "Cyrus Beck");
    pair<int, int> vertices[]
        = { make_pair(200, 50),
            make_pair(250, 100),
            make_pair(200, 150),
            make_pair(100, 150),
            make_pair(50, 100),
            make_pair(100, 50) };
  
    // Make sure that the vertices
    // are put in a clockwise order
    int n = sizeof(vertices) / sizeof(vertices[0]);
    pair<int, int> line[] = { make_pair(10, 10), make_pair(450, 200) };
    pair<int, int>* temp1 = CyrusBeck(vertices, line, n);
    pair<int, int> temp2[2];
    temp2[0] = line[0];
    temp2[1] = line[1];
  
    // To allow clipping and unclipping
    // of the line by just pressing a key
    bool trigger = false;
    while (window.isOpen()) {
        window.clear();
        Event event;
        if (window.pollEvent(event)) {
            if (event.type == Event::Closed)
                window.close();
            if (event.type == Event::KeyPressed)
                trigger = !trigger;
        }
        drawPolygon(&window, vertices, n);
  
        // Using the trigger value to clip
        // and unclip a line
        if (trigger) {
            line[0] = temp1[0];
            line[1] = temp1[1];
        }
        else {
            line[0] = temp2[0];
            line[1] = temp2[1];
        }
        drawline(&window, line[0], line[1]);
        window.display();
    }
    return 0;
}

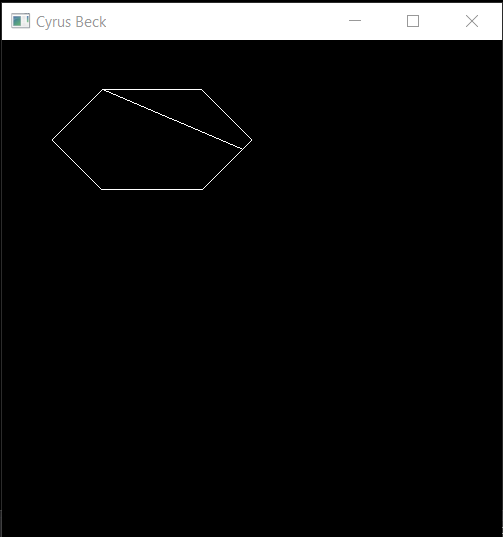
Producción:

(102, 50) (240, 109)

Antes de recortar:
Después del recorte:

Publicación traducida automáticamente

Artículo escrito por xlms2065 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta