Recuento de formas de elegir N personas con al menos X hombres y Y mujeres de P Hombres y Q mujeres

Dados los números enteros N, P, Q, X e Y, la tarea es encontrar el número de formas de formar un grupo de N personas que tenga al menos X hombres e Y mujeres de P hombres y Q mujeres, donde (X + Y ≤ N, X ≤ P e Y ≤ Q).

Ejemplos:

Entrada: P = 4, Q = 2, N = 5, X = 3, Y = 1
Salida: 6
Explicación: Suponga que el grupo dado es {m1, m2, m3, m4} y {w1, w2}. Entonces las combinaciones posibles son:
m1 m2 m3 m4 w1
m1 m2 m3 m4 w2
m1 m2 m3 w1 w2
m1 m2 m4 w1 w2
m1 m3 m4 w1 w2
m2 m3 m4 w1 w2
Por lo tanto, la cuenta es 6.

Entrada: P = 5, Q = 2, N = 6, X = 4, Y = 1
Salida: 7

Enfoque ingenuo: este problema se basa en la combinatoria , y los detalles del enfoque ingenuo ya se analizan en el Conjunto 1 de este problema.

Para algún valor general de P, Q, N, X e Y podemos calcular el total de formas posibles utilizando la siguiente fórmula:

$_{X}^{P}\textrm{C} \ast _{N-X}^{Q}\textrm{C} + _{X+1}^{P}\textrm{C} \ast _{N-X-1}^{Q}\textrm{C} + . . . + _{N-Y+1}^{P}\textrm{C} \ast _{Y-1}^{Q}\textrm{C} + _{N-Y}^{P}\textrm{C} \ast _{Y}^{Q}\textrm{C}$

dónde

$_{r}^{n}\textrm{C} = \frac{n!}{r!*(n-r)!}$

En este enfoque, en cada paso estábamos calculando el valor de cada forma posible.

Complejidad de Tiempo: O(N ² )
Espacio Auxiliar: O(1)

Enfoque eficiente: para resolver este problema de manera eficiente, podemos usar la propiedad del Triángulo de Pascal para calcular el $_{r}^{n}\textrm{C}$ , es decir

1
1 1
1 2 1
1 3 3 1
.
.
.

que no es más que

$_{0}^{0}\textrm{C}$
$_{0}^{1}\textrm{C}$    $_{1}^{1}\textrm{C}$
$_{0}^{2}\textrm{C}$    $_{1}^{2}\textrm{C}$    $_{2}^{2}\textrm{C}$
$_{0}^{3}\textrm{C}$    $_{1}^{3}\textrm{C}$    $_{2}^{3}\textrm{C}$    $_{3}^{3}\textrm{C}$
.
.
.

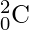
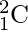
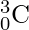
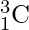
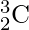
Siga los pasos que se mencionan a continuación:

Utilice el triángulo pascal para precalcular los valores de la combinación.
Comience iterando un ciclo desde i = X hasta i = P y haga lo siguiente para cada iteración.
Comprobar si (Ni) ≥ Y y (Ni) ≤ Q .
Si se cumple la condición, cuente las formas posibles para i hombres y (Ni) mujeres , de lo contrario, omita el paso.
Suma el conteo con el número total de formas.
Devuelva el recuento total como su respuesta.

A continuación se muestra la implementación del enfoque:

C++

#include <bits/stdc++.h>
using namespace std;
 
long long int pascal[31][31];
 
// Function to calculate the pascal triangle
void pascalTriangle()
{
    pascal[0][0] = 1;
    pascal[1][0] = 1;
    pascal[1][1] = 1;
 
    // Loop to calculate values of
    // pascal triangle
    for (int i = 2; i < 31; i++) {
        pascal[i][0] = 1;
        for (int j = 1; j < i; j++)
            pascal[i][j]
                = pascal[i - 1][j]
                  + pascal[i - 1][j - 1];
        pascal[i][i] = 1;
    }
}
 
// Function to calculate the number of ways
long long int countWays(int n, int p,
                        int q, int x,
                        int y)
{
 
    // Variable to store the answer
    long long int sum = 0;
 
    // Loop to calculate the number of ways
    for (long long int i = x; i <= p; i++) {
        if (n - i >= y && n - i <= q)
            sum += pascal[p][i]
                   * pascal[q][n - i];
    }
    return sum;
}
 
// Driver code
int main()
{
    pascalTriangle();
 
    int P = 4, Q = 2, N = 5, X = 3, Y = 1;
 
    // Calculate possible ways for given
    // N, P, Q, X and Y
    cout << countWays(N, P, Q, X, Y)
         << endl;
    return 0;
}

Java

// Java code for the above approach
import java.io.*;
class GFG {
 
    static long pascal[][] = new long[31][31];
 
    // Function to calculate the pascal triangle
    static void pascalTriangle()
    {
        pascal[0][0] = 1;
        pascal[1][0] = 1;
        pascal[1][1] = 1;
 
        // Loop to calculate values of
        // pascal triangle
        for (int i = 2; i < 31; i++) {
            pascal[i][0] = 1;
            for (int j = 1; j < i; j++)
                pascal[i][j] = pascal[i - 1][j]
                               + pascal[i - 1][j - 1];
            pascal[i][i] = 1;
        }
    }
 
    // Function to calculate the number of ways
    static long countWays(int n, int p, int q, int x, int y)
    {
 
        // Variable to store the answer
        long sum = 0;
 
        // Loop to calculate the number of ways
        for (int i = x; i <= p; i++) {
            if (n - i >= y && n - i <= q)
                sum += pascal[p][i] * pascal[q][n - i];
        }
        return sum;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        pascalTriangle();
        int P = 4, Q = 2, N = 5, X = 3, Y = 1;
 
        // Calculate possible ways for given
        // N, P, Q, X and Y
        System.out.println(countWays(N, P, Q, X, Y));
    }
}
 
// This code is contributed by Potta Lokesh

Python3

pascal = [[0 for i in range(31)] for j in range(31)]
 
# Function to calculate the pascal triangle
def pascalTriangle():
  pascal[0][0] = 1;
  pascal[1][0] = 1;
  pascal[1][1] = 1;
 
  # Loop to calculate values of
  # pascal triangle
  for i in range(2, 31):
    pascal[i][0] = 1;
    for j in range(i):
      pascal[i][j] = pascal[i - 1][j] + pascal[i - 1][j - 1];
    pascal[i][i] = 1;
 
# Function to calculate the number of ways
def countWays(n, p, q, x, y):
 
  # Variable to store the answer
  sum = 0;
 
  # Loop to calculate the number of ways
  for i in range(x, p + 1):
    if (n - i >= y and n - i <= q):
      sum += pascal[p][i] * pascal[q][n - i];
  return sum;
 
# Driver code
pascalTriangle();
 
P = 4
Q = 2
N = 5
X = 3
Y = 1;
 
# Calculate possible ways for given
# N, P, Q, X and Y
print(countWays(N, P, Q, X, Y))
 
# This code is contributed by Saurabh Jaiswal

C#

// C# code for the above approach
using System;
 
class GFG{
 
static long [,]pascal = new long[31, 31];
 
// Function to calculate the pascal triangle
static void pascalTriangle()
{
    pascal[0, 0] = 1;
    pascal[1, 0] = 1;
    pascal[1, 1] = 1;
 
    // Loop to calculate values of
    // pascal triangle
    for(int i = 2; i < 31; i++)
    {
        pascal[i, 0] = 1;
        for(int j = 1; j < i; j++)
            pascal[i, j] = pascal[i - 1, j] +
                           pascal[i - 1, j - 1];
        pascal[i, i] = 1;
    }
}
 
// Function to calculate the number of ways
static long countWays(int n, int p, int q, int x, int y)
{
     
    // Variable to store the answer
    long sum = 0;
 
    // Loop to calculate the number of ways
    for(int i = x; i <= p; i++)
    {
        if (n - i >= y && n - i <= q)
            sum += pascal[p, i] * pascal[q, n - i];
    }
    return sum;
}
 
// Driver code
public static void Main(String[] args)
{
    pascalTriangle();
     
    int P = 4, Q = 2, N = 5, X = 3, Y = 1;
 
    // Calculate possible ways for given
    // N, P, Q, X and Y
    Console.WriteLine(countWays(N, P, Q, X, Y));
}
}
 
// This code is contributed by shikhasingrajput

Javascript

<script>
let pascal = new Array(31).fill(0).map(() => new Array(31).fill(0));
 
// Function to calculate the pascal triangle
function pascalTriangle() {
  pascal[0][0] = 1;
  pascal[1][0] = 1;
  pascal[1][1] = 1;
 
  // Loop to calculate values of
  // pascal triangle
  for (let i = 2; i < 31; i++) {
    pascal[i][0] = 1;
    for (let j = 1; j < i; j++)
      pascal[i][j]
        = pascal[i - 1][j]
        + pascal[i - 1][j - 1];
    pascal[i][i] = 1;
  }
}
 
// Function to calculate the number of ways
function countWays(n, p, q, x, y) {
 
  // Variable to store the answer
  let sum = 0;
 
  // Loop to calculate the number of ways
  for (let i = x; i <= p; i++) {
    if (n - i >= y && n - i <= q)
      sum += pascal[p][i]
        * pascal[q][n - i];
  }
  return sum;
}
 
// Driver code
pascalTriangle();
 
let P = 4, Q = 2, N = 5, X = 3, Y = 1;
 
// Calculate possible ways for given
// N, P, Q, X and Y
document.write(countWays(N, P, Q, X, Y))
 
// This code is contributed by gfgking.
</script>

Producción

Tiempo Complejidad: O(N)
Espacio Auxiliar: O(N ² )

Publicación traducida automáticamente

Artículo escrito por Code_r y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Recuento de formas de elegir N personas con al menos X hombres y Y mujeres de P Hombres y Q mujeres | conjunto 2

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta