Recuento de formas de elegir N personas que contengan al menos 4 niños y 1 niña de P niños y Q niñas

Dados los números enteros N , P y Q , la tarea es encontrar el número de formas de formar un grupo de N personas que tenga al menos 4 niños y 1 niña de P niños y Q niñas .

Ejemplos:

Entrada: P = 5, Q = 2, N = 5
Salida: 10
Explicación: Suponga que el grupo dado es {m1, m2, m3, m4, m5} y {w1, w2}. Entonces las posibles combinaciones son:

m1 m2 m3 m4 w1
m2 m3 m4 m5 w1
m1 m3 m4 m5 w1
m1 m2 m4 m5 w1
m1 m2 m3 m5 w1
m1 m2 m3 m4 w2
m2 m3 m4 m5 w2
m1 m3 m4 m5 w2
m1 m2 m4 m5 w2
m1 m2 m3 m5 w2

Por lo tanto, la cuenta es 10.

Entrada: P = 5, Q = 2, N = 6
Salida: 7

Enfoque: este problema se basa en la combinatoria donde necesitamos seleccionar al menos 4 niños de 1 niño disponible, y al menos Y niñas de Q niñas disponibles, de modo que el total de personas seleccionadas sea N.
Considere el ejemplo:

P = 5, Q = 2, N = 6
En este, las selecciones posibles son:
(4 niños de 5) * (2 niñas de 2) + (5 niños de 5) * (1 niña de 2)
= 5C4 * 2C2 + 5C5 * 2C1

Entonces, para algunos valores generales de P , Q y N , el enfoque se puede visualizar como:

$_{4}^{P}\textrm{C} \ast _{N-4}^{Q}\textrm{C} + _{5}^{P}\textrm{C} \ast _{N-5}^{Q}\textrm{C} + . . . + _{N-2}^{P}\textrm{C} \ast _{2}^{Q}\textrm{C} + _{N-1}^{P}\textrm{C} \ast _{1}^{Q}\textrm{C}$
where
$_{r}^{n}\textrm{C} = \frac{n!}{r!*(n-r)!}$

Siga los pasos mencionados a continuación para implementarlo:

Comience a iterar un ciclo desde i = 4 hasta i = P .
En cada iteración, calcule el número de formas posibles si elegimos i niños y (Ni) niñas, usando la combinación
$_{i}^{P}\textrm{C} \ast _{N-i}^{Q}\textrm{C}$
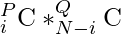
Agregue el valor posible para cada iteración como el número total de formas.
Devuelve el total de formas calculadas al final.

A continuación se muestra la implementación del enfoque:

C++

#include <bits/stdc++.h>
using namespace std;
 
// Function to calculate factorial
long long int fact(int f)
{
    f++;
    long long int ans = 1;
 
    // Loop to calculate factorial of f
    while (--f > 0)
        ans = ans * f;
    return ans;
}
 
// Function to calculate combination nCr
long long int ncr(int n, int r)
{
    return (fact(n) / (fact(r) * fact(n - r)));
}
 
// Function to calculate the number of ways
long long int countWays(int n, int p, int q)
{
    long long int sum = 0;
 
    // Loop to calculate the number of ways
    for (long long int i = 4; i <= p; i++) {
        if (n - i >= 1 && n - i <= q)
            sum += (ncr(p, i) * ncr(q, n - i));
    }
    return sum;
}
 
// Driver code
int main()
{
    int P = 5, Q = 2, N = 5;
    cout << countWays(N, P, Q) << endl;
    return 0;
}

Java

import java.util.*;
 
class GFG{
 
// Function to calculate factorial
static int fact(int f)
{
    f++;
    int ans = 1;
 
    // Loop to calculate factorial of f
    while (--f > 0)
        ans = ans * f;
    return ans;
}
 
// Function to calculate combination nCr
static int ncr(int n, int r)
{
    return (fact(n) / (fact(r) * fact(n - r)));
}
 
// Function to calculate the number of ways
static int countWays(int n, int p, int q)
{
    int sum = 0;
 
    // Loop to calculate the number of ways
    for (int i = 4; i <= p; i++) {
        if (n - i >= 1 && n - i <= q)
            sum += (ncr(p, i) * ncr(q, n - i));
    }
    return sum;
}
 
// Driver code
public static void main(String[] args)
{
    int P = 5, Q = 2, N = 5;
    System.out.print(countWays(N, P, Q) +"\n");
}
}
 
// This code is contributed by 29AjayKumar

Python3

# Function to calculate factorial
def fact(f):
    ans = 1
 
    # Loop to calculate factorial of f
    while (f):
        ans = ans * f
        f -= 1
    return ans
 
# Function to calculate combination nCr
def ncr(n, r):
    return (fact(n) / (fact(r) * fact(n - r)))
 
# Function to calculate the number of ways
def countWays(n, p, q):
    sum = 0
 
    # Loop to calculate the number of ways
    for i in range(4, p + 1):
        if (n - i >= 1 and n - i <= q):
            sum += (ncr(p, i) * ncr(q, n - i))
 
    return (int)(sum)
 
# Driver code
P = 5
Q = 2
N = 5
print(countWays(N, P, Q))
 
 # This code is contributed by gfgking.

C#

// C# program for the above approach
using System;
using System.Collections.Generic;
 
class GFG {
 
// Function to calculate factorial
static int fact(int f)
{
    f++;
    int ans = 1;
 
    // Loop to calculate factorial of f
    while (--f > 0)
        ans = ans * f;
    return ans;
}
 
// Function to calculate combination nCr
static int ncr(int n, int r)
{
    return (fact(n) / (fact(r) * fact(n - r)));
}
 
// Function to calculate the number of ways
static int countWays(int n, int p, int q)
{
    int sum = 0;
 
    // Loop to calculate the number of ways
    for (int i = 4; i <= p; i++) {
        if (n - i >= 1 && n - i <= q)
            sum += (ncr(p, i) * ncr(q, n - i));
    }
    return sum;
}
 
    // Driver Code
    public static void Main()
    {
        int P = 5, Q = 2, N = 5;
        Console.Write(countWays(N, P, Q));
    }
}
 
// This code is contributed by sanjoy_62.

Javascript

<script>
 
    // Function to calculate factorial
    const fact = (f) => {
        f++;
        let ans = 1;
 
        // Loop to calculate factorial of f
        while (--f > 0)
            ans = ans * f;
        return ans;
    }
 
    // Function to calculate combination nCr
    const ncr = (n, r) => {
        return (fact(n) / (fact(r) * fact(n - r)));
    }
 
    // Function to calculate the number of ways
    const countWays = (n, p, q) => {
        let sum = 0;
 
        // Loop to calculate the number of ways
        for (let i = 4; i <= p; i++) {
            if (n - i >= 1 && n - i <= q)
                sum += (ncr(p, i) * ncr(q, n - i));
        }
        return sum;
    }
 
    // Driver code
 
    let P = 5, Q = 2, N = 5;
    document.write(countWays(N, P, Q));
 
    // This code is contributed by rakeshsahni
 
</script>

Producción

Complejidad de Tiempo: O(N ² )
Espacio Auxiliar: O(1)

Publicación traducida automáticamente

Artículo escrito por Code_r y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta