Recuento de inversiones mediante estructura de datos basada en políticas

Requisito previo: estructura de datos basada en políticas

Dada una array arr[] , la tarea es encontrar el número de inversiones para cada elemento de la array.

Recuento de inversión: para una array indica qué tan lejos (o cerca) está la array de ser ordenada. Si la array ya está ordenada, el conteo de inversión es 0. Si la array está ordenada en orden inverso, entonces el conteo de inversión es el máximo.

Formalmente, Número de índices y tal que y .

Ejemplos:

Entrada: {5, 2, 3, 2, 3, 8, 1}
Salida: {0, 1, 1, 2, 1, 0, 6}
Explicación:
Cuenta de inversión para cada elemento –
Elemento en el índice 0: No hay elementos con índice menor que 0, que es mayor que arr[0].
Elemento en el índice 1: Hay un elemento con un índice menor que 1, que es mayor que 2. Eso es 5.
Elemento en el índice 2: Hay un elemento con un índice menor que 2, que es mayor que 3. Eso es 5.
Elemento en el índice 3: Hay dos elementos con un índice menor que 3, que es mayor que 2. Eso es 5, 3.
Elemento en el índice 4: Hay un elemento con un índice menor que 4, que es mayor que 3. Eso es 5.
Elemento en índice 5: No hay elementos con índice menor a 5, que es mayor a 8.
Elemento en el índice 6: Hay seis elementos con un índice menor que 6, que es mayor que 1. Eso es 5, 2, 3, 2, 3

Entrada: arr[] = {3, 2, 1}
Salida: {0, 1, 2}

Acercarse:

• Cree una estructura de datos basada en políticas de tipo par.
• Itere la array dada y realice los siguientes pasos:
  • Aplicar order_of_key({X, N+1}) para cada elemento X donde N es el tamaño de la array.
    Nota: order_of_key no es más que lower_bound. Además, usamos N+1 porque es mayor que todos los índices de la array.
  • Deje que order_of_key resulte ser l, entonces el conteo de inversión para el elemento actual será igual a 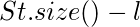lo que en última instancia es el conteo de elementos más pequeños que X y llegaron antes de X en la array.
  • Inserte el elemento actual X junto con su índice en la estructura de datos basada en políticas St. El índice se inserta junto con cada elemento para su identificación única en el conjunto y para tratar con duplicados.

A continuación se muestra la implementación del enfoque anterior:

// C++ implementation to find the
// Inversion Count using Policy
// Based Data Structure
  
#include <bits/stdc++.h>
  
// Header files for policy based
// data structure which are
// to be included
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
  
using namespace __gnu_pbds;
using namespace std;
  
typedef tree<pair<int, int>, null_type,
             less<pair<int, int> >, rb_tree_tag,
             tree_order_statistics_node_update>
    new_data_set;
  
// Function to find the inversion count
// of the elements of the array
void inversionCount(int arr[], int n)
{
    int ans[n];
  
    // Making a new policy based data
    // structure which will
    // store pair<int, int>
    new_data_set St;
  
    // Loop to iterate over the elements
    // of the array
    for (int i = 0; i < n; i++) {
  
        // Now to find lower_bound of
        // the element X, we will use pair
        // as {x, n+1} to cover all the
        // elements and even the duplicates
        int cur = St.order_of_key({ arr[i],
                                    n + 1 });
  
        ans[i] = St.size() - cur;
  
        // Store element along with index
        St.insert({ arr[i], i });
    }
  
    for (int i = 0; i < n; i++) {
        cout << ans[i] << " ";
    }
    cout << "\n";
}
  
// Driver Code
int main()
{
    int arr[] = { 5, 2, 3, 2, 3, 8, 1 };
    int n = sizeof(arr) / sizeof(int);
  
    // Function Call
    inversionCount(arr, n);
  
    return 0;
}

0 1 1 2 1 0 6

Complejidad del tiempo: