Recuento de Nodes que tienen divisores impares en el subárbol dado para consultas Q

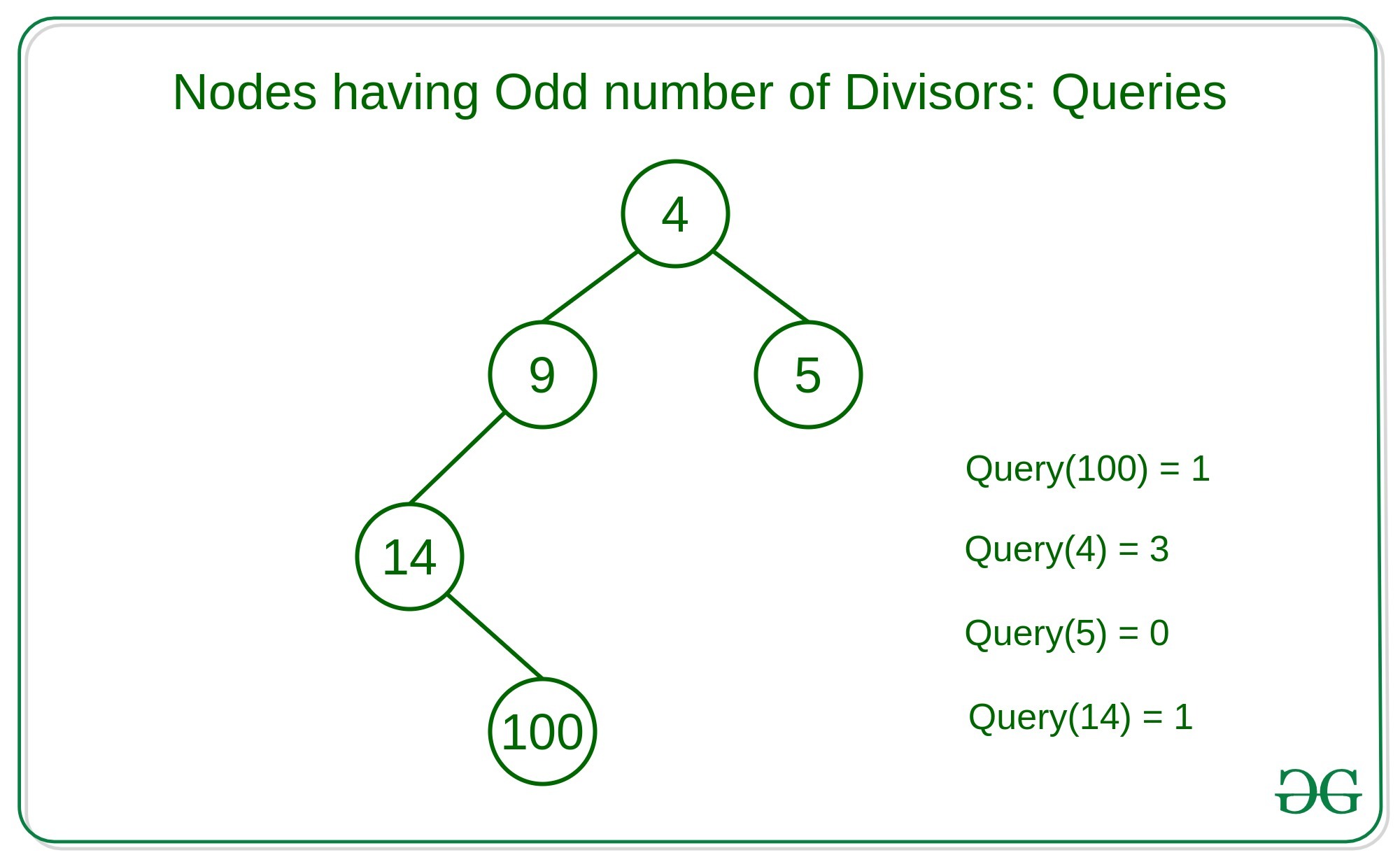
Dado un árbol N-ario y consultas Q donde cada consulta contiene un Node del árbol N-ario, la tarea es contar el número de Nodes que tienen un número impar de divisores en el subárbol para consultas Q. 

Ejemplos: 

Aporte: 
 

Salida: 1 3 0 1 

Explicación:  
Consulta 1: En el subárbol con raíz en el Node 100, solo hay un Node que es 100 que tiene 9 divisores {1, 2, 4, 5, 10, 20, 25, 50, 100}. Por lo tanto, solo hay un Node que tiene el número impar de divisores. 
Consulta 2: en el subárbol con raíz en el Node 4, hay 5 Nodes de los cuales 3 Nodes tienen un número impar de divisores. Eso es {4, 9, 100} 
Consulta 3: En el subárbol con raíz en el Node 5, solo hay un Node que es 5 que tiene dos divisores. Por lo tanto, hay cero Nodes que tienen un número impar de divisores. 

Enfoque ingenuo: una solución simple es recorrer el subárbol para cada consulta y encontrar el recuento de Nodes que tienen un número impar de divisores.

Enfoque eficiente: la idea es calcular previamente el recuento de un número impar de divisores para cada subárbol y almacenar el recuento en hash-map . Para precalcular el conteo de Nodes que tienen un número impar de divisores, podemos usar el recorrido de búsqueda primero en profundidad . Finalmente, para verificar si el Node actual tiene un número impar de divisores o no, podemos usar el hecho de que todo número cuadrado perfecto tiene un número impar de divisores.

A continuación se muestra la implementación del enfoque anterior:

// C++ implementation to count the
// number of nodes having odd
// number of divisors for each query
 
#include <bits/stdc++.h>
using namespace std;
 
#define N 100001
 
// Adjacency list
// for tree.
vector<int> adj[N];
 
// Array for values and
// answer at ith node.
int a[N], ans[N];
 
// Function to check whether N
// has odd divisors or not
bool hasOddNumberOfDivisors(int n)
{
    if ((double)sqrt(n) == (int)sqrt(n))
        return true;
    return false;
}
 
// DFS function to pre-compute
// the answers
int dfs(int node, int parent)
{
    // Initialize the count
    int count = 0;
    for (auto i = adj[node].begin(); i != adj[node].end();
         ++i) {
        if (*i != parent) {
 
            // Repeat for every child
            count += dfs(*i, node);
        }
    }
 
    // Increase the count if current node
    // has odd number of divisors
    if (hasOddNumberOfDivisors(a[node]))
        ++count;
 
    ans[node] = count;
    return count;
}
 
// Driver Code
int main()
{
 
    int n = 5, i;
    vector<int> q = { 4, 1, 5, 3 };
 
    // Adjacency List
    adj[1].push_back(2);
    adj[2].push_back(1);
    adj[2].push_back(3);
    adj[3].push_back(2);
    adj[3].push_back(4);
    adj[4].push_back(3);
    adj[1].push_back(5);
    adj[5].push_back(1);
 
    a[1] = 4;
    a[2] = 9;
    a[3] = 14;
    a[4] = 100;
    a[5] = 5;
 
    // Function call
    dfs(1, -1);
 
    for (int i = 0; i < q.size(); i++) {
        cout << ans[q[i]] << " ";
    }
    return 0;
}

// Java implementation to
// count the number of nodes
// having odd number of
// divisors for each query
import java.util.*;
class GFG{
 
static final int N = 100001;
 
// Adjacency list
// for tree.
static Vector<Integer> []adj =
              new Vector[N];
 
// Array for values and
// answer at ith node.
static int []a = new int[N];
static int []ans = new int[N];
 
// Function to check whether N
// has odd divisors or not
static boolean hasOddNumberOfDivisors(int n)
{
  if ((double)Math.sqrt(n) ==
      (int)Math.sqrt(n))
    return true;
  return false;
}
 
// DFS function to
// pre-compute the answers
static int dfs(int node,
               int parent)
{
  // Initialize the count
  int count = 0;
  for (int i : adj[node])
  {
    if (i != parent)
    {
      // Repeat for every child
      count += dfs(i, node);
    }
  }
 
  // Increase the count if
  // current node has odd
  // number of divisors
  if (hasOddNumberOfDivisors(a[node]))
    ++count;
 
  ans[node] = count;
  return count;
}
 
// Driver Code
public static void main(String[] args)
{
  int n = 5;
  int[] q = {4, 1, 5, 3};
   
  for (int i = 0; i < adj.length; i++)
    adj[i] = new Vector<Integer>();
   
  // Adjacency List
  adj[1].add(2);
  adj[2].add(1);
  adj[2].add(3);
  adj[3].add(2);
  adj[3].add(4);
  adj[4].add(3);
  adj[1].add(5);
  adj[5].add(1);
 
  a[1] = 4;
  a[2] = 9;
  a[3] = 14;
  a[4] = 100;
  a[5] = 5;
 
  // Function call
  dfs(1, -1);
 
  for (int i = 0; i < q.length; i++)
  {
    System.out.print(ans[q[i]] + " ");
  }
}
}
 
// This code is contributed by Rajput-Ji

# Python3 implementation to count the
# number of nodes having odd
# number of divisors for each query
import math
 
N = 100001
  
# Adjacency list
# for tree.
adj = [[] for i in range(N)]
  
# Array for values and
# answer at ith node.
a = [0 for i in range(N)]
 
ans = [0 for i in range(N)]
  
# Function to check whether N
# has odd divisors or not
def hasOddNumberOfDivisors(n):
 
    if (math.sqrt(n) == int(math.sqrt(n))):
        return True
         
    return False
  
# DFS function to pre-compute
# the answers
def dfs(node, parent):
 
    # Initialize the count
    count = 0
     
    for i in adj[node]:
        if (i != parent):
  
            # Repeat for every child
            count += dfs(i, node)
             
    # Increase the count if current node
    # has odd number of divisors
    if (hasOddNumberOfDivisors(a[node])):
        count += 1
  
    ans[node] = count
     
    return count
 
# Driver Code
if __name__=="__main__":
  
    n = 5
    i = 0
     
    q = [ 4, 1, 5, 3 ]
  
    # Adjacency List
    adj[1].append(2)
    adj[2].append(1)
    adj[2].append(3)
    adj[3].append(2)
    adj[3].append(4)
    adj[4].append(3)
    adj[1].append(5)
    adj[5].append(1)
  
    a[1] = 4
    a[2] = 9
    a[3] = 14
    a[4] = 100
    a[5] = 5
     
    # Function call
    dfs(1, -1)
     
    for i in range(len(q)):
        print(ans[q[i]], end = ' ')
  
# This code is contributed by rutvik_56

// C# implementation to
// count the number of nodes
// having odd number of
// divisors for each query
using System;
using System.Collections.Generic;
class GFG{
 
static readonly int N = 100001;
 
// Adjacency list
// for tree.
static List<int> []adj =
            new List<int>[N];
 
// Array for values and
// answer at ith node.
static int []a = new int[N];
static int []ans = new int[N];
 
// Function to check whether N
// has odd divisors or not
static bool hasOddNumberOfDivisors(int n)
{
  if ((double)Math.Sqrt(n) ==
      (int)Math.Sqrt(n))
    return true;
  return false;
}
 
// DFS function to
// pre-compute the answers
static int dfs(int node,
               int parent)
{
  // Initialize the count
  int count = 0;
  foreach (int i in adj[node])
  {
    if (i != parent)
    {
      // Repeat for every child
      count += dfs(i, node);
    }
  }
 
  // Increase the count if
  // current node has odd
  // number of divisors
  if (hasOddNumberOfDivisors(a[node]))
    ++count;
 
  ans[node] = count;
  return count;
}
 
// Driver Code
public static void Main(String[] args)
{
  int n = 5;
  int[] q = {4, 1, 5, 3};
   
  for (int i = 0;
           i < adj.Length; i++)
    adj[i] = new List<int>();
   
  // Adjacency List
  adj[1].Add(2);
  adj[2].Add(1);
  adj[2].Add(3);
  adj[3].Add(2);
  adj[3].Add(4);
  adj[4].Add(3);
  adj[1].Add(5);
  adj[5].Add(1);
 
  a[1] = 4;
  a[2] = 9;
  a[3] = 14;
  a[4] = 100;
  a[5] = 5;
 
  // Function call
  dfs(1, -1);
 
  for (int i = 0;
           i < q.Length; i++)
  {
    Console.Write(ans[q[i]] + " ");
  }
}
}
 
// This code is contributed by Rajput-Ji

<script>
    // Javascript implementation to
    // count the number of nodes
    // having odd number of
    // divisors for each query
     
    let N = 100001;
  
    // Adjacency list
    // for tree.
    let adj = new Array(N);
 
    // Array for values and
    // answer at ith node.
    let a = new Array(N);
    let ans = new Array(N);
 
    // Function to check whether N
    // has odd divisors or not
    function hasOddNumberOfDivisors(n)
    {
      if (Math.sqrt(n) == parseInt(Math.sqrt(n), 10))
        return true;
      return false;
    }
 
    // DFS function to
    // pre-compute the answers
    function dfs(node, parent)
    {
      // Initialize the count
      let count = 0;
      for (let i = 0; i < adj[node].length; i++)
      {
        if (adj[node][i] != parent)
        {
          // Repeat for every child
          count += dfs(adj[node][i], node);
        }
      }
 
      // Increase the count if
      // current node has odd
      // number of divisors
      if (hasOddNumberOfDivisors(a[node]))
        ++count;
 
      ans[node] = count;
      return count;
    }
     
    let n = 5;
    let q = [4, 1, 5, 3];
 
    for (let i = 0; i < adj.length; i++)
      adj[i] = [];
 
    // Adjacency List
    adj[1].push(2);
    adj[2].push(1);
    adj[2].push(3);
    adj[3].push(2);
    adj[3].push(4);
    adj[4].push(3);
    adj[1].push(5);
    adj[5].push(1);
 
    a[1] = 4;
    a[2] = 9;
    a[3] = 14;
    a[4] = 100;
    a[5] = 5;
 
    // Function call
    dfs(1, -1);
 
    for (let i = 0; i < q.length; i++)
    {
      document.write(ans[q[i]] + " ");
    }
 
// This code is contributed by decode2207.
</script>

1 3 0 1