Recuento de pares en Array con diferencia igual a la diferencia con dígitos invertidos

Dado un arreglo arr[] de N enteros, la tarea es encontrar el número de pares de elementos del arreglo (arr[i], arr[j]) tales que la diferencia entre los pares sea igual a la diferencia cuando los dígitos de ambos los números están invertidos. 

Ejemplos:

Entrada: arr[] = {42, 11, 1, 97}
Salida: 2
Explicación:
Los pares válidos de elementos de array son (42, 97), (11, 1) como:
1. 42 – 97 = 24 – 79 = (-55)
2. 11 – 1 = 11 – 1 = (10)

Entrada: arr[] = {1, 2, 3, 4}
Salida: 6

Enfoque: el problema dado se puede resolver utilizando Hashing , que se basa en las siguientes observaciones:

Un par válido (i, j) seguirá la ecuación como

=> arr[i] – arr[j] = rev(arr[i]) – rev(arr[j]) =
> arr[i] – rev(arr[i]) = arr[j] – rev(arr [j])

Siga los pasos a continuación para resolver el problema:

• Ahora, cree una función reverseDigits , que tomará un número entero como argumento e invertirá los dígitos de ese número entero.
• Almacene la frecuencia de los valores arr[i] – rev(arr[i]) en un mapa desordenado , digamos mp .
• Para cada clave (= diferencia) de frecuencia X, el número de pares que se pueden formar viene dado por  .
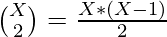• El recuento total de pares viene dado por la suma del valor de la expresión anterior para cada frecuencia almacenada en el mapa mp .

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to reverse the digits
// of an integer
int reverseDigits(int n)
{
    // Convert the given number
    // to a string
    string s = to_string(n);
 
    // Reverse the string
    reverse(s.begin(), s.end());
 
    // Return the value of the string
    return stoi(s);
}
int countValidPairs(vector<int> arr)
{
    // Stores resultant count of pairs
    long long res = 0;
 
    // Stores the frequencies of
    // differences
    unordered_map<int, int> mp;
    for (int i = 0; i < arr.size(); i++) {
        mp[arr[i] - reverseDigits(arr[i])]++;
    }
 
    // Traverse the map and count pairs
    // formed for all frequency values
    for (auto i : mp) {
        long long int t = i.second;
        res += t * (t - 1) / 2;
    }
 
    // Return the resultant count
    return res;
}
 
// Driver Code
int main()
{
    vector<int> arr = { 1, 2, 3, 4 };
    cout << countValidPairs(arr);
 
    return 0;
}

// Java program for the above approach
import java.util.HashMap;
 
class GFG {
 
    // Function to reverse the digits
    // of an integer
    public static int reverseDigits(int n)
    {
       
        // Convert the given number
        // to a string
        String s = String.valueOf(n);
 
        // Reverse the string
        s = new StringBuffer(s).reverse().toString();
 
        // Return the value of the string
        return Integer.parseInt(s);
    }
 
    public static int countValidPairs(int[] arr)
    {
       
        // Stores resultant count of pairs
        int res = 0;
 
        // Stores the frequencies of
        // differences
        HashMap<Integer, Integer> mp = new HashMap<Integer, Integer>();
        for (int i = 0; i < arr.length; i++) {
            if (mp.containsKey(arr[i] - reverseDigits(arr[i]))) {
                mp.put(arr[i] - reverseDigits(arr[i]), mp.get(arr[i] - reverseDigits(arr[i])) + 1);
            } else {
                mp.put(arr[i] - reverseDigits(arr[i]), 1);
            }
        }
 
        // Traverse the map and count pairs
        // formed for all frequency values
        for (int i : mp.keySet()) {
            int t = mp.get(i);
            res += t * (t - 1) / 2;
        }
 
        // Return the resultant count
        return res;
    }
 
    // Driver Code
    public static void main(String args[])
    {
        int[] arr = { 1, 2, 3, 4 };
        System.out.println(countValidPairs(arr));
    }
 
}
 
// This code is contributed by saurabh_jaiswal.

# python program for the above approach
 
# Function to reverse the digits
# of an integer
def reverseDigits(n):
 
    # Convert the given number
    # to a string
    s = str(n)
 
    # Reverse the string
    s = "".join(reversed(s))
 
    # Return the value of the string
    return int(s)
 
def countValidPairs(arr):
 
    # Stores resultant count of pairs
    res = 0
 
    # Stores the frequencies of
    # differences
    mp = {}
 
    for i in range(0, len(arr)):
        if not arr[i] - reverseDigits(arr[i]) in mp:
            mp[arr[i] - reverseDigits(arr[i])] = 1
        else:
            mp[arr[i] - reverseDigits(arr[i])] += 1
 
        # Traverse the map and count pairs
        # formed for all frequency values
    for i in mp:
        t = mp[i]
        res += (t * (t - 1)) // 2
 
        # Return the resultant count
    return res
 
# Driver Code
if __name__ == "__main__":
 
    arr = [1, 2, 3, 4]
    print(countValidPairs(arr))
 
    # This code is contributed by rakeshsahni

// C# program for the above approach
using System;
using System.Collections.Generic;
 
class GFG {
 
    // Function to reverse the digits
    // of an integer
    public static int reverseDigits(int n)
    {
 
        // Convert the given number
        // to a string
        string s = n.ToString();
 
        // Reverse the string
        char[] arr = s.ToCharArray();
        Array.Reverse(arr);
        string st = new string(arr);
 
        // Return the value of the string
        return Int32.Parse(st);
    }
 
    public static int countValidPairs(int[] arr)
    {
 
        // Stores resultant count of pairs
        int res = 0;
 
        // Stores the frequencies of
        // differences
        Dictionary<int, int> mp
            = new Dictionary<int, int>();
        for (int i = 0; i < arr.Length; i++) {
            if (mp.ContainsKey(arr[i]
                               - reverseDigits(arr[i]))) {
                mp[arr[i] - reverseDigits(arr[i])]
                    = mp[arr[i] - reverseDigits(arr[i])]
                      + 1;
            }
            else {
                mp[arr[i] - reverseDigits(arr[i])] = 1;
            }
        }
 
        // Traverse the map and count pairs
        // formed for all frequency values
        foreach(int i in mp.Keys)
        {
            int t = mp[i];
            res += t * (t - 1) / 2;
        }
 
        // Return the resultant count
        return res;
    }
 
    // Driver Code
    public static void Main()
    {
        int[] arr = { 1, 2, 3, 4 };
        Console.WriteLine(countValidPairs(arr));
    }
}
 
// This code is contributed by ukasp.

<script>
// Javascript program for the above approach
 
// Function to reverse the digits
// of an integer
function reverseDigits(n)
{
 
  // Convert the given number
  // to a string
  let s = new String(n);
 
  // Reverse the string
  s = s.split("").reverse().join("");
 
  // Return the value of the string
  return parseInt(s);
}
function countValidPairs(arr)
{
 
  // Stores resultant count of pairs
  let res = 0;
 
  // Stores the frequencies of
  // differences
  let mp = new Map();
  for (let i = 0; i < arr.length; i++) {
    let temp = arr[i] - reverseDigits(arr[i]);
    if (mp.has(temp)) {
      mp.set(temp, mp.get(temp) + 1);
    } else {
      mp.set(temp, 1);
    }
  }
 
  // Traverse the map and count pairs
  // formed for all frequency values
  for (i of mp) {
    let t = i[1];
    res += (t * (t - 1)) / 2;
  }
 
  // Return the resultant count
  return res;
}
 
// Driver Code
let arr = [1, 2, 3, 4];
document.write(countValidPairs(arr));
 
// This code is contributed by gfgking.
</script>

6

Complejidad temporal: O(N)
Espacio auxiliar: O(N)