Dada una array arr de tamaño N , la tarea es encontrar el número de sus permutaciones tal que la suma de MEX de sus arrays de prefijos sea máxima.
Nota: MEX de un conjunto de enteros se define como el menor entero no negativo que no pertenece a este conjunto.
Ejemplo:
Entrada: arr[] = {1, 0, 1}
Salida: 2
Explicación:
Todas las permutaciones y sus MEX son las siguientes:
[0, 1, 2] => array: {1, 0, 1}, MEX({1 }) + MEX({1, 0}) + MEX({1, 0, 1}) = 0 + 2 + 2 = 4
[0, 2, 1] => array: {1, 1, 0}, MEX ({1}) + MEX({1, 1}) + MEX({1, 1, 0}) = 0 + 0 + 2 = 2
[1, 0, 2] => array: {0, 1, 1 }, MEX({0}) + MEX({0, 1}) + MEX({0, 1, 1}) = 1 + 2 + 2 = 5
[1, 2, 0] => array: {0, 1, 1}, MEX({0}) + MEX({0, 1}) + MEX({0, 1, 1}) = 1 + 2 + 2 = 5
[2, 0, 1] => array: {1, 1, 0}, MÉXICO({1}) + MÉXICO({1, 1}) + MÉXICO({1, 1, 0}) = 0 + 0 + 2 = 2
[2, 1, 0] = > array: {1, 0, 1}, MEX({1}) + MEX({1, 0}) + MEX({1, 0, 1}) = 0 + 2 + 2 = 4
Por lo tanto, la suma máxima es 5 y el número de permutaciones con esta suma es 2.Entrada: arr[] = {0, 1, 2, 2, 5, 6}
Salida: 12
Acercarse:
La idea óptima se basa en la observación de que la suma de MEX de las arrays de prefijos será máxima cuando todos los elementos distintos estén dispuestos en orden creciente y los duplicados estén presentes al final de la array (como 0, 1, 2, 3, …). Una vez que se rompe esta continuidad, el MEX del resto, después de ese punto, sigue siendo el mismo. Por ejemplo, en {0, 1, 2, 2, 5, 6}, los MEX de las arrays de prefijos son {1, 2, 3, 3, 3, 3} en los que la continuidad se rompe en el índice 3.
Ahora, para encontrar el recuento de todas las permutaciones con la suma máxima de MEX, almacene la frecuencia de los elementos en un mapa. En una array de prefijos MEX máximos, la primera posición siempre se llena con 0, luego la segunda con 1, la tercera con 2 y así sucesivamente. Así que trate de completarlos con el número de opciones disponibles y una vez que se alcance el punto donde se rompe la continuidad, el MEX de todas las permutaciones después de ese punto es el mismo y los elementos después de este se pueden organizar en cualquier permutación posible. Ahora, para entenderlo mejor, digamos que hay números de 0 a Y presentes en la array, luego se rompe la continuidad y después de eso, hay K elementos más presentes. Entonces el conteo de permutaciones con suma máxima de MEX es:
ans = frecuencia[0] * frecuencia[1] * frecuencia[2] * … * frecuencia[Y] * factorial[K]
Ahora, en el caso de {0, 1, 2, 2, 5, 6}, la array que tiene la suma máxima de MEX de sus arrays de prefijos puede:
- Solo contiene 0 en el índice 0, por lo que el número de opciones para el primer índice es 1.
- Solo contiene 1 en el índice 1, por lo que el número de opciones aquí es 1.
- Contenga cualquiera de los dos 2 presentes, por lo que el número de opciones aquí es 2.
- Ahora, después de esto, la continuidad se rompe y los elementos posteriores se pueden organizar en cualquier orden:
- Entonces, el número total de opciones después de este punto es
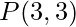 , es decir
, es decir 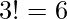 .
.
- Entonces, el número total de opciones después de este punto es
- Ahora, el número final de todas las permutaciones es
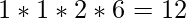 .
.
Siga los pasos a continuación para resolver el problema:
- Declare un mapa mp para almacenar la frecuencia de los elementos.
- Ahora cree una variable cnt para realizar un seguimiento de los elementos presentes a la derecha de un elemento e inicialícelo con N, es decir, el número total de elementos presentes.
- También declare una variable ans para almacenar la respuesta e inicialícela con 1.
- Ahora comience a iterar desde 0 hasta el tamaño de la array dada, es decir, desde i = 0 hasta i < n:
- Si mp[i] != 0, esto significa que la continuidad prevalece hasta este punto y se deben considerar todas las opciones posibles (es decir, mp[i]). Entonces, ans se convertirá en ans=ans*mp[i] y reducirá cnt en 1 para obtener los elementos presentes a la derecha del siguiente elemento.
- Si mp[i] == 0, esto significa que aquí se rompe la continuidad y los elementos posteriores se pueden organizar en cualquier permutación posible. Entonces, rompe el bucle aquí y considera todas las permutaciones posibles para los elementos presentes a la derecha de este punto, es decir, factorial de cnt.
- Escriba la respuesta de acuerdo con la observación anterior.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// To calculate the factorial
int factorial(int n)
{
int res = 1, i;
for (i = 2; i <= n; i++) {
res *= i;
}
return res;
}
// To return the number of permutations of
// an array with maximum MEXs sum of prefix array
int countPermutations(int ar[], int n)
{
// Map to store the frequency of each element
unordered_map<int, int> mp;
int ans = 1, cnt = n;
for (int i = 0; i < n; i++) {
mp[ar[i]]++;
}
// Running a loop from i=0 to i<n
for (int i = 0; i < n; i++) {
// If continuity breaks,
// then break the loop
if (mp[i] == 0) {
break;
}
// Considering choices available to be
// filled at this position, i.e. mp[i]
ans = (ans * mp[i]);
// Decrement the count of remaining
// right elements
cnt--;
}
// Adding all permutations of the
// elements present to the right of
// the point where continuity breaks.
ans = ans * factorial(cnt);
return ans;
}
// Driver Code
int main()
{
int arr[] = { 1, 0, 1 };
int N = sizeof(arr) / sizeof(arr[0]);
cout << countPermutations(arr, N);
}
Java
// java program for the above approach
import java.util.*;
class GFG
{
// To calculate the factorial
static int factorial(int n)
{
int res = 1, i;
for (i = 2; i <= n; i++) {
res *= i;
}
return res;
}
// To return the number of permutations of
// an array with maximum MEXs sum of prefix array
static int countPermutations(int[] ar, int n)
{
// Map to store the frequency of each element
Map<Integer, Integer> mp= new HashMap<Integer, Integer>();
int ans = 1, cnt = n, i;
for (i = 0; i < n; i++) {
if (mp.containsKey(ar[i]))
{
mp.put(ar[i],mp.get(ar[i])+1);
}
else
{
mp.put(ar[i], 1);
}
}
// Running a loop from i=0 to i<n
for (i = 0; i < n; i++) {
// If continuity breaks,
// then break the loop
if (! mp.containsKey(i)) {
break;
}
// Considering choices available to be
// filled at this position, i.e. mp[i]
ans = (ans * mp.get(i));
// Decrement the count of remaining
// right elements
cnt--;
}
// Adding all permutations of the
// elements present to the right of
// the point where continuity breaks.
ans = ans * factorial(cnt);
return ans;
}
// Driver Code
public static void main(String[] args)
{
int[] arr = { 1, 0, 1 };
int N = arr.length;
System.out.print(countPermutations(arr, N));
}
}
// This code is contributed by amreshkumar3.
Python3
# Python Program to implement # the above approach # To calculate the factorial def factorial(n): res = 1 for i in range(2, n + 1): res *= i return res # To return the number of permutations of # an array with maximum MEXs sum of prefix array def countPermutations(ar, n): # Map to store the frequency of each element mp = dict() ans = 1 cnt = n for i in range(n): if (ar[i] in mp): mp[ar[i]] += 1 else: mp[ar[i]] = 1 # Running a loop from i=0 to i<n for i in range(n): # If continuity breaks, # then break the loop if (i not in mp): break # Considering choices available to be # filled at this position, i.e. mp[i] ans = (ans * mp[i]) # Decrement the count of remaining # right elements cnt -= 1 # Adding all permutations of the # elements present to the right of # the point where continuity breaks. ans = ans * factorial(cnt) return ans # Driver Code arr = [1, 0, 1] N = len(arr) print(countPermutations(arr, N)) # This code is contributed by gfgking
C#
// C# program for the above approach
using System;
using System.Collections.Generic;
public class GFG
{
// To calculate the factorial
static int factorial(int n)
{
int res = 1, i;
for (i = 2; i <= n; i++) {
res *= i;
}
return res;
}
// To return the number of permutations of
// an array with maximum MEXs sum of prefix array
static int countPermutations(int[] ar, int n)
{
// Map to store the frequency of each element
Dictionary<int, int> mp = new Dictionary<int, int>();
int ans = 1, cnt = n, i;
for (i = 0; i < n; i++) {
if (mp.ContainsKey(ar[i]))
{
mp[ar[i]] = mp[ar[i]] + 1;
}
else
{
mp.Add(ar[i], 1);
}
}
// Running a loop from i=0 to i<n
for (i = 0; i < n; i++) {
// If continuity breaks,
// then break the loop
if (! mp.ContainsKey(i)) {
break;
}
// Considering choices available to be
// filled at this position, i.e. mp[i]
ans = (ans * mp[i]);
// Decrement the count of remaining
// right elements
cnt--;
}
// Adding all permutations of the
// elements present to the right of
// the point where continuity breaks.
ans = ans * factorial(cnt);
return ans;
}
// Driver Code
public static void Main(String[] args)
{
int[] arr = { 1, 0, 1 };
int N = arr.Length;
Console.Write(countPermutations(arr, N));
}
}
// This code is contributed by code_hunt.
Javascript
<script>
// JavaScript Program to implement
// the above approach
// To calculate the factorial
function factorial(n) {
let res = 1, i;
for (i = 2; i <= n; i++) {
res *= i;
}
return res;
}
// To return the number of permutations of
// an array with maximum MEXs sum of prefix array
function countPermutations(ar, n) {
// Map to store the frequency of each element
let mp = new Map();
let ans = 1, cnt = n;
for (let i = 0; i < n; i++) {
if (mp.has(ar[i])) {
mp.set(ar[i], mp.get(ar[i]) + 1)
}
else {
mp.set(ar[i], 1)
}
}
// Running a loop from i=0 to i<n
for (let i = 0; i < n; i++) {
// If continuity breaks,
// then break the loop
if (!mp.has(i)) {
break;
}
// Considering choices available to be
// filled at this position, i.e. mp[i]
ans = (ans * mp.get(i));
// Decrement the count of remaining
// right elements
cnt--;
}
// Adding all permutations of the
// elements present to the right of
// the point where continuity breaks.
ans = ans * factorial(cnt);
return ans;
}
// Driver Code
let arr = [1, 0, 1];
let N = arr.length
document.write(countPermutations(arr, N));
// This code is contributed by Potta Lokesh
</script>
2
Complejidad temporal: O(N)
Espacio auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por ramandeep8421 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA