Recuento de polígonos anidados que se pueden dibujar uniendo vértices internamente

Dado un polígono regular de N lados. La tarea es encontrar la cantidad de polígonos que se pueden extraer del polígono dado uniendo internamente los vértices del polígono dado.

Ejemplos:

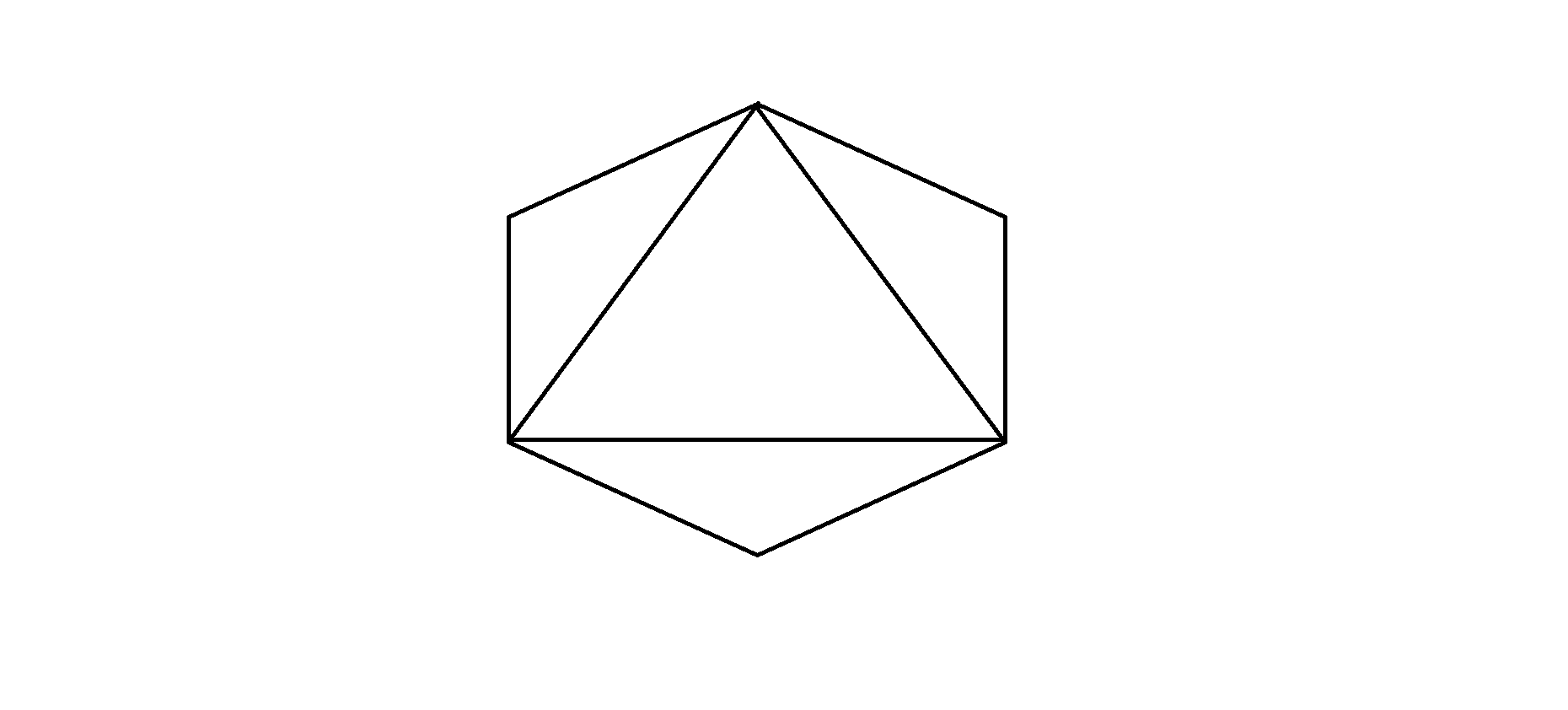
Entrada: N = 6
Salida: 1
Explicación:

Solo hay un polígono anidado, es decir, Triángulo cuyos lados son las cuerdas del polígono padre inmediato, es decir, Hexágono.

Entrada: N = 12
Salida: 2
Explicación: 

Hay dos polígonos anidados. El primero es un hexágono y el segundo es un triángulo. Los lados de ambos polígonos anidados son en realidad cuerdas de su polígono padre inmediato.

Planteamiento: Para resolver este problema observe lo siguiente:

1. Los polígonos con un número de lados menor o igual a 5 no pueden producir polígonos anidados, es decir, los polígonos de lados ≤5 siempre tendrán al menos un lado superpuesto con su polígono anidado.
2. Cada lado de un polígono anidado toma dos lados consecutivos del polígono padre inmediato.

Con las observaciones anteriores, es fácil concluir que el número de lados de cada polígono anidado es la mitad del número de lados de su polígono padre inmediato. Entonces, seguimos dividiendo N por 2 e incrementamos el contador para polígonos anidados, hasta que N sea menor o igual a 5.

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
 
#include <iostream>
using namespace std;
 
// Function that counts the nested
// polygons inside another polygons
int countNestedPolygons(int sides)
{
    // Stores the count
    int count = 0;
 
    // Child polygons can only existss
    // if parent polygon has sides > 5
    while (sides > 5) {
 
        // Get next nested polygon
        sides /= 2;
        count += 1;
    }
 
    // Return the count
    return count;
}
 
// Driver Code
int main()
{
    // Given side of polygon
    int N = 12;
 
    // Function Call
    cout << countNestedPolygons(N);
 
    return 0;
}

// Java program for the above approach
class GFG{
 
// Function that counts the nested
// polygons inside another polygons
static int countNestedPolygons(int sides)
{
    // Stores the count
    int count = 0;
 
    // Child polygons can only existss
    // if parent polygon has sides > 5
    while (sides > 5)
    {
 
        // Get next nested polygon
        sides /= 2;
        count += 1;
    }
 
    // Return the count
    return count;
}
 
// Driver Code
public static void main(String[] args)
{
    // Given side of polygon
    int N = 12;
 
    // Function Call
    System.out.print(countNestedPolygons(N));
}
}
 
// This code is contributed by Rajput-Ji

# Python3 program for the above approach
 
# Function that counts the nested
# polygons inside another polygons
def countNestedPolygons(sides):
 
    # Stores the count
    count = 0
 
    # Child polygons can only exists
    # if parent polygon has sides > 5
    while (sides > 5):
 
        # Get next nested polygon
        sides //= 2
        count += 1
 
    # Return the count
    return count
 
# Driver Code
 
# Given side of polygon
N = 12
 
# Function call
print(countNestedPolygons(N))
 
# This code is contributed by vishu2908

// C# program for the above approach
using System;
 
class GFG{
 
// Function that counts the nested
// polygons inside another polygons
static int countNestedPolygons(int sides)
{
     
    // Stores the count
    int count = 0;
 
    // Child polygons can only existss
    // if parent polygon has sides > 5
    while (sides > 5)
    {
 
        // Get next nested polygon
        sides /= 2;
        count += 1;
    }
 
    // Return the count
    return count;
}
 
// Driver Code
public static void Main(String[] args)
{
     
    // Given side of polygon
    int N = 12;
 
    // Function call
    Console.Write(countNestedPolygons(N));
}
}
 
// This code is contributed by Rajput-Ji

<script>
 
// JavaScript program for the above approach
// Function that counts the nested
// polygons inside another polygons
function countNestedPolygons(sides)
{
    // Stores the count
    var count = 0;
 
    // Child polygons can only existss
    // if parent polygon has sides > 5
    while (sides > 5)
    {
 
        // Get next nested polygon
        sides /= 2;
        count += 1;
    }
 
    // Return the count
    return count;
}
 
// Driver Code
// Given side of polygon
var N = 12;
 
// Function Call
document.write(countNestedPolygons(N));
 
// This code contributed by shikhasingrajput
 
</script>

2

Complejidad de tiempo: O (log N), donde N es el número de vértices en el polígono dado.
Espacio Auxiliar: O(1)