Recuento de strings binarias de longitud N que tienen como máximo M 1 o 0 consecutivos, alternativamente, exactamente K veces

Posted on by Rudeus Greyrat

Dados tres números enteros, N, K y M. La tarea es encontrar el número de strings binarias de longitud N que siempre comienza con 1 , en las que puede haber como máximo M 1 o 0 consecutivos y se alternan exactamente K veces.
Ejemplos: 
 

Entrada: N = 5, K = 3, M = 2 
Salida: 3 
Las 3 configuraciones son: 
11001 
10011 
11011 
Explicación: 
Observe que los grupos de 1 y 0 se alternan exactamente K veces
Entrada: N = 7, K = 4, M = 3 
Salida: 16 
 

Enfoque: dado que este problema involucra tanto subproblemas superpuestos como subestructuras óptimas . Entonces, este problema se puede resolver usando programación dinámica .
 

  • Subproblema : DP[i][j] representa el número de strings binarias hasta la longitud i que tienen j grupos alternos hasta ahora. Entonces, para calcular dp[N][K] si conocemos el valor de dp[nj][k-1], podemos obtener fácilmente el resultado sumando el valor del subproblema sobre j = 1 a m (DP [N][K] representa la respuesta final).
    Como se muestra a continuación en el diagrama de árbol de recurrencia, se observan muchas superposiciones de subproblemas. Por lo tanto, el resultado debe almacenarse en caché para evitar cálculos redundantes. 
     

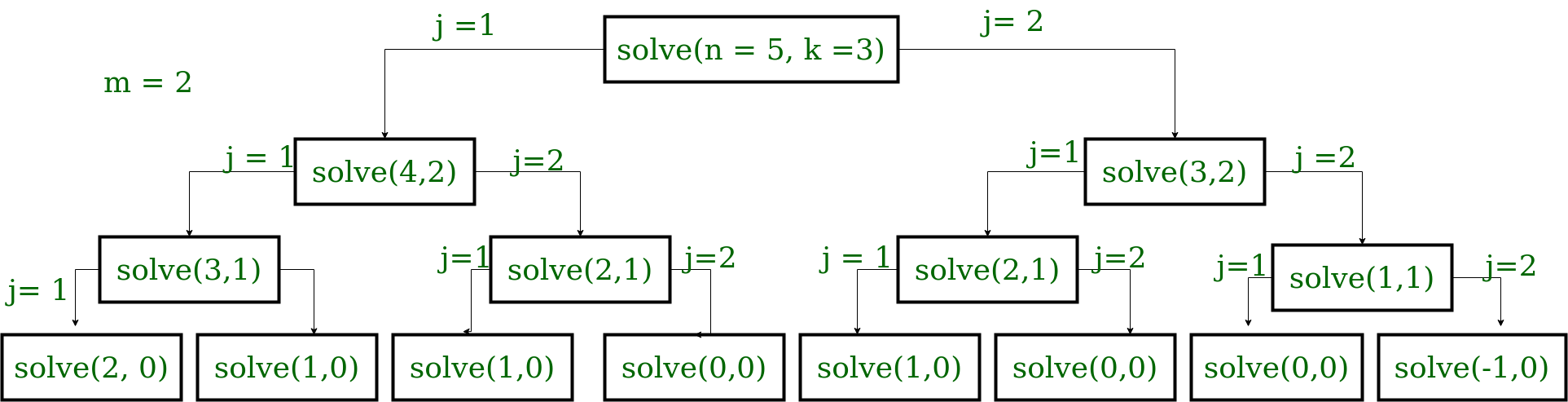
  • Subestructura óptima: 
    $dp[i][j]=$$\sum_{j=1}^{M} f(Nj, K-1)
     
  • Siguiendo el enfoque de DP de arriba hacia abajo: 
    como podemos tener un grupo que puede tener como máximo la longitud M , iteramos en cada longitud posible y recurrimos con una nueva N y disminuyendo K en 1, a medida que se forma un nuevo grupo. La solución al subproblema se almacena en caché y se resume para dar el resultado final dp[N][K]. 
     
  • Caso base: 
    1. Cuando N es 0 y K es 0, devuelve 1
    2. Cuando N es 0 pero K no es 0, devuelve 0
    3. Cuando N no es 0 pero K es 0, devuelve 0
    4. Cuando ambos son negativos, devuelve 0

A continuación se muestra la implementación del enfoque anterior: 
 

C++

// C++ program to find the count
// of Binary strings of length N
// having atmost M consecutive 1s or 0s
// alternatively exactly K times
 
#include <bits/stdc++.h>
using namespace std;
 
// Array to contain the final result
int dp[1000][1000];
 
// Function to get the number
// of desirable binary strings
int solve(int n, int k, int m)
{
 
    // if we reach end of string
    // and groups are exhausted,
    // return 1
    if (n == 0 && k == 0)
        return 1;
 
    // if length is exhausted but
    // groups are still to be made,
    // return 0
    if (n == 0 && k != 0)
        return 0;
 
    // if length is not exhausted
    // but groups are exhausted,
    // return 0
    if (n != 0 && k == 0)
        return 0;
 
    // if both are negative
    // just return 0
    if (n < 0 || k < 0)
        return 0;
 
    // if already calculated,
    // return it
    if (dp[n][k])
        return dp[n][k];
 
    // initialise answer
    // for each state
    int ans = 0;
 
    // loop through every
    // possible m
    for (int j = 1; j <= m; j++) {
        ans += solve(n - j, k - 1, m);
    }
    return dp[n][k] = ans;
}
 
// Driver code
int main()
{
 
    int N = 7, K = 4, M = 3;
    cout << solve(N, K, M);
}

Java

// Java program to find the count of
// Binary Strings of length N having
// atmost M consecutive 1s or 0s
// alternatively exactly K times
import java.util.*;
 
class GFG{
 
// Array to contain the final result
static int [][]dp = new int[1000][1000];
 
// Function to get the number
// of desirable binary strings
static int solve(int n, int k, int m)
{
 
    // If we reach end of string
    // and groups are exhausted,
    // return 1
    if (n == 0 && k == 0)
        return 1;
 
    // If length is exhausted but
    // groups are still to be made,
    // return 0
    if (n == 0 && k != 0)
        return 0;
 
    // If length is not exhausted
    // but groups are exhausted,
    // return 0
    if (n != 0 && k == 0)
        return 0;
 
    // If both are negative
    // just return 0
    if (n < 0 || k < 0)
        return 0;
 
    // If already calculated,
    // return it
    if (dp[n][k] > 0)
        return dp[n][k];
 
    // Initialise answer
    // for each state
    int ans = 0;
 
    // Loop through every
    // possible m
    for(int j = 1; j <= m; j++)
    {
       ans += solve(n - j, k - 1, m);
    }
    return dp[n][k] = ans;
}
 
// Driver code
public static void main(String[] args)
{
    int N = 7, K = 4, M = 3;
    System.out.print(solve(N, K, M));
}
}
 
// This code is contributed by Rajput-Ji

Python 3

# Python3 program to find the count
# of Binary strings of length N
# having atmost M consecutive 1s or
# 0s alternatively exactly K times
 
# List to contain the final result
rows, cols = (1000, 1000)
dp = [[0 for i in range(cols)]
         for j in range(rows)]
 
# Function to get the number
# of desirable binary strings
def solve(n, k, m):
     
    # If we reach end of string
    # and groups are exhausted,
    # return 1
    if n == 0 and k == 0:
        return 1
 
    # If length is exhausted but
    # groups are still to be made,
    # return 0
    if n == 0 and k != 0:
        return 0
 
    # If length is not exhausted
    # but groups are exhausted,
    # return 0
    if n != 0 and k == 0:
        return 0
 
    # If both are negative
    # just return 0
    if n < 0 or k < 0:
        return 0
 
    # If already calculated,
    # return it
    if dp[n][k]:
        return dp[n][k]
 
    # Initialise answer
    # for each state
    ans = 0
 
    # Loop through every
    # possible m
    for j in range(1, m + 1):
        ans = ans + solve(n - j,
                          k - 1, m)
    dp[n][k] = ans
     
    return dp[n][k]
 
# Driver code
N = 7
K = 4
M = 3
 
print(solve(N, K, M))
 
# This code is contributed by ishayadav181

C#

// C# program to find the count of
// binary strings of length N having
// atmost M consecutive 1s or 0s
// alternatively exactly K times
using System;
 
class GFG{
 
// Array to contain the readonly result
static int [,]dp = new int[1000, 1000];
 
// Function to get the number
// of desirable binary strings
static int solve(int n, int k, int m)
{
 
    // If we reach end of string
    // and groups are exhausted,
    // return 1
    if (n == 0 && k == 0)
        return 1;
 
    // If length is exhausted but
    // groups are still to be made,
    // return 0
    if (n == 0 && k != 0)
        return 0;
 
    // If length is not exhausted
    // but groups are exhausted,
    // return 0
    if (n != 0 && k == 0)
        return 0;
 
    // If both are negative
    // just return 0
    if (n < 0 || k < 0)
        return 0;
 
    // If already calculated,
    // return it
    if (dp[n, k] > 0)
        return dp[n, k];
 
    // Initialise answer
    // for each state
    int ans = 0;
 
    // Loop through every
    // possible m
    for(int j = 1; j <= m; j++)
    {
       ans += solve(n - j, k - 1, m);
    }
    return dp[n, k] = ans;
}
 
// Driver code
public static void Main(String[] args)
{
    int N = 7, K = 4, M = 3;
     
    Console.Write(solve(N, K, M));
}
}
 
// This code is contributed by gauravrajput1

Javascript

<script>
 
// Javascript program to find the count of
// Binary Strings of length N having
// atmost M consecutive 1s or 0s
// alternatively exactly K times
 
    // Array to contain the final result
     dp = Array(1000);
     for(i =0;i<1000;i++)
         dp[i] = Array(1000).fill(0);
 
    // Function to get the number
    // of desirable binary strings
    function solve(n , k , m)
    {
 
        // If we reach end of string
        // and groups are exhausted,
        // return 1
        if (n == 0 && k == 0)
            return 1;
 
        // If length is exhausted but
        // groups are still to be made,
        // return 0
        if (n == 0 && k != 0)
            return 0;
 
        // If length is not exhausted
        // but groups are exhausted,
        // return 0
        if (n != 0 && k == 0){
            return 0;
            }
 
        // If both are negative
        // just return 0
        if (n < 0 || k < 0)
            return 0;
 
        // If already calculated,
        // return it
        if (dp[n][k] > 0)
            return dp[n][k];
 
        // Initialise answer
        // for each state
        var ans = 0;
 
        // Loop through every
        // possible m
        for (var j = 1; j <= m; j++) {
            ans += solve(n - j, k - 1, m);
           // document.write(ans);
        }
        return dp[n][k] = ans;
    }
 
    // Driver code
     
        var N = 7, K = 4, M = 3;
        document.write(solve(N, K, M));
 
// This code contributed by umadevi9616
 
</script>
Producción: 

16

 

Complejidad de tiempo: O(N*K*M)
 Espacio auxiliar: O(1000*1000)

Publicación traducida automáticamente

Artículo escrito por VikasVishwakarma1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *