Dado un arreglo arr[] con elementos positivos y negativos, la tarea es contar todos los subarreglos cuya suma sea un cuadrado perfecto.
Ejemplos:
Entrada: arr[] = {2, 3, -5, 6, -7, 4};
Salida: 5
Explicación:
Subarreglos {2, 3, -5}, {-5, 6}, {3, -5, 6}, {3, -5, 6, -7, 4} y {4} con suma es 0, 1, 4, 1 y 4 respectivamente tienen suma cuadrada perfecta.Entrada: arr[] = {3, -6, 4, -2, 7};
Salida: 3
Explicación: {3, -6, 4}, {4}, {4, -2, 7} son los subarreglos con suma cuadrada perfecta.
Enfoque ingenuo:
una solución simple sería generar todos los subarreglos posibles. Mientras se desplaza, realice un seguimiento de la suma del subarreglo. Lleve un recuento de todos los subarreglos cuya suma sea un cuadrado perfecto.
Solución eficiente: la idea es usar una array de suma de prefijos para resolver el problema dado.
- Cree una array prefixSum y almacene su suma de prefijos.
- Atraviese la array prefixSum e identifique su valor mínimo, es decir ( prefixMin ).
- Ahora, cree un mapa desordenado que se pueda usar para almacenar la frecuencia de prefixSum actual, mientras recorre la array prefixSum .
- Inicialice el índice clave 0 del mapa con el valor 1, ya que 0 es un cuadrado perfecto.
- Atraviese la array prefixSum con un bucle anidado.
- Para cada elemento prefixSum, el bucle anidado encontrará mapKey = (prefixSum[i] – j*j) , si está disponible en el índice del mapa.
- Si (prefixSum[i] – j*j) ya está disponible en el mapa, actualizamos nuestro contador con el valor de índice de (prefixSum[i] – j*j) .
- La idea es verificar el valor actual de prefixSum con todos los cuadrados (j*j) hasta que la diferencia llegue a prefixMin .
- Ahora, incremente el mapa con el índice del prefixSum actual en 1 con cada iteración del ciclo externo.
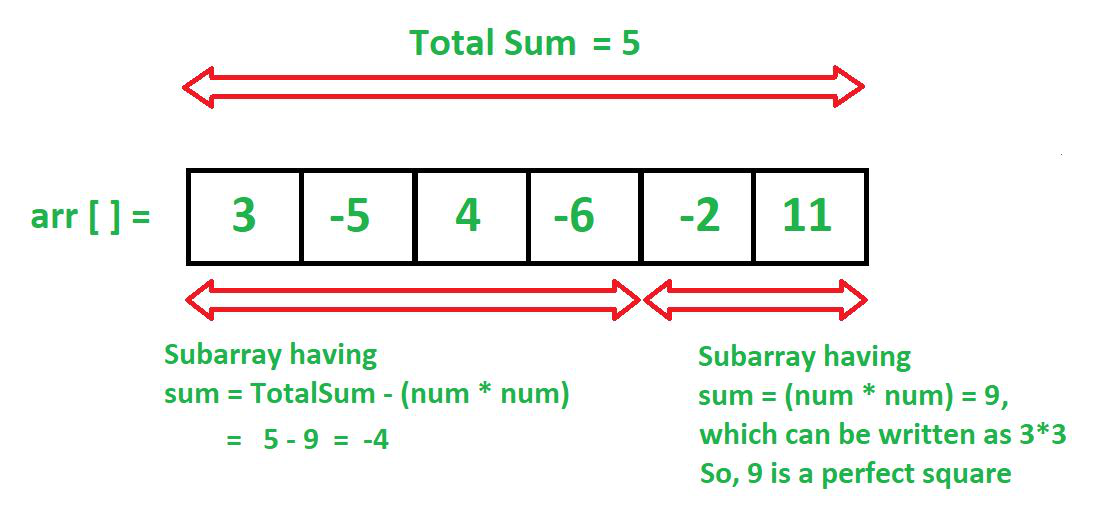
- El concepto subyacente es que seguimos buscando desde (prefixSum[i] – j*j ) porque, si una parte es la array es (prefixSum[i] – j*j ) , entonces la otra parte de la array sería (j *j) es decir, una suma de cuadrados perfectos.
- Puede ver en el diagrama anterior que totalSum es en realidad el prefixSum, que se usa para ese propósito.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ code for the above approach.
#include <bits/stdc++.h>
using namespace std;
#define lli long long int
// Function to find count of subarrays
// whose sum is a perfect square.
lli countSubarrays(int arr[],
int n)
{
// to search for index with
// (current prefix sum - j*j)
unordered_map<int, int> mp;
// storing the prefix sum
int prefixSum[n];
// used to track the minimum
// value in prefixSum
int prefixMin = 0;
prefixSum[0] = arr[0];
prefixMin = min(prefixMin,
prefixSum[0]);
// Calculating the prefixSum
// and tracking the prefixMin
for (int i = 1; i < n; i++) {
prefixSum[i] = prefixSum[i - 1]
+ arr[i];
// below statement is used if
// array contains
// negative numbers
prefixMin = min(prefixMin,
prefixSum[i]);
}
// counts the no of subarrays
// with perfect square sum
lli countSubs = 0;
// as 0 is a perfect square,
// so we initialize 0th
// index-key with value 1
mp[0] = 1;
// Here we count the perfect
// square subarray sum by
// searching if there is a
// prefix with
// sum = (current prefixSum - (sq*sq))
for (int i = 0; i < n; i++) {
for (int j = 0;
prefixSum[i] - j * j >= prefixMin;
j++) {
if (mp.find(prefixSum[i] - j * j)
!= mp.end())
// increasing our subarray count
countSubs += mp[prefixSum[i]
- j * j];
}
// increasing the current prefixSum
// index value in map by 1 to count
// the other perfect squares while
// traversing further
mp[prefixSum[i]]++;
}
return countSubs;
}
// Driver code
int main()
{
int arr[] = { 2, 3, -5,
6, -7, 4 };
int n = sizeof(arr) / sizeof(arr[0]);
lli ans = countSubarrays(arr, n);
// printing the result
cout << ans;
return 0;
}
Java
// Java code for
// the above approach.
import java.util.*;
class GFG{
// Function to find count of
// subarrays whose sum is
// a perfect square.
static long countSubarrays(int arr[],
int n)
{
// To search for index with
// (current prefix sum - j*j)
HashMap<Integer,
Integer> mp = new HashMap<Integer,
Integer>();
// Storing the prefix sum
int []prefixSum = new int[n];
// Used to track the minimum
// value in prefixSum
int prefixMin = 0;
prefixSum[0] = arr[0];
prefixMin = Math.min(prefixMin,
prefixSum[0]);
// Calculating the prefixSum
// and tracking the prefixMin
for (int i = 1; i < n; i++)
{
prefixSum[i] = prefixSum[i - 1] + arr[i];
// Below statement is used if
// array contains
// negative numbers
prefixMin = Math.min(prefixMin,
prefixSum[i]);
}
// Counts the no of subarrays
// with perfect square sum
long countSubs = 0;
// As 0 is a perfect square,
// so we initialize 0th
// index-key with value 1
mp.put(0, 1);
// Here we count the perfect
// square subarray sum by
// searching if there is a
// prefix with
// sum = (current prefixSum - (sq*sq))
for (int i = 0; i < n; i++)
{
for (int j = 0;
prefixSum[i] - j *
j >= prefixMin; j++)
{
if (mp.containsKey(prefixSum[i] - j * j))
// Increasing our subarray count
countSubs += mp.get(prefixSum[i] -
j * j);
}
// Increasing the current prefixSum
// index value in map by 1 to count
// the other perfect squares while
// traversing further
if(mp.containsKey(prefixSum[i]))
{
mp.put(prefixSum[i],
mp.get(prefixSum[i]) + 1);
}
else
{
mp.put(prefixSum[i], 1);
}
}
return countSubs;
}
// Driver code
public static void main(String[] args)
{
int arr[] = {2, 3, -5,
6, -7, 4};
int n = arr.length;
long ans = countSubarrays(arr, n);
// Printing the result
System.out.print(ans);
}
}
// This code is contributed by Princi Singh
Python3
# Python3 code for the above approach. from collections import defaultdict # Function to find count of subarrays # whose sum is a perfect square. def countSubarrays(arr, n): # To search for index with # (current prefix sum - j*j) mp = defaultdict(lambda:0) # Storing the prefix sum prefixSum = [0] * n # Used to track the minimum # value in prefixSum prefixMin = 0 prefixSum[0] = arr[0] prefixMin = min(prefixMin, prefixSum[0]) # Calculating the prefixSum # and tracking the prefixMin for i in range(1, n): prefixSum[i] = prefixSum[i - 1] + arr[i] # Below statement is used if # array contains negative numbers prefixMin = min(prefixMin, prefixSum[i]) # Counts the no of subarrays # with perfect square sum countSubs = 0 # As 0 is a perfect square, # so we initialize 0th # index-key with value 1 mp[0] = 1 # Here we count the perfect # square subarray sum by # searching if there is a # prefix with # sum = (current prefixSum - (sq*sq)) for i in range(n): j = 0 while prefixSum[i] - j * j >= prefixMin: if prefixSum[i] - j * j in mp: # Increasing our subarray count countSubs += mp[prefixSum[i] - j * j] j += 1 # Increasing the current prefixSum # index value in map by 1 to count # the other perfect squares while # traversing further mp[prefixSum[i]] += 1 return countSubs # Driver code arr = [ 2, 3, -5, 6, -7, 4 ] n = len(arr) ans = countSubarrays(arr, n) # Printing the result print(ans) # This code is contributed by Shivam Singh
C#
// C# code for
// the above approach.
using System;
using System.Collections.Generic;
class GFG{
// Function to find count of
// subarrays whose sum is
// a perfect square.
static long countSubarrays(int []arr,
int n)
{
// To search for index with
// (current prefix sum - j*j)
Dictionary<int,
int> mp =
new Dictionary<int,
int>();
// Storing the prefix sum
int []prefixSum = new int[n];
// Used to track the minimum
// value in prefixSum
int prefixMin = 0;
prefixSum[0] = arr[0];
prefixMin = Math.Min(prefixMin,
prefixSum[0]);
// Calculating the prefixSum
// and tracking the prefixMin
for (int i = 1; i < n; i++)
{
prefixSum[i] = prefixSum[i - 1] +
arr[i];
// Below statement is used if
// array contains
// negative numbers
prefixMin = Math.Min(prefixMin,
prefixSum[i]);
}
// Counts the no of subarrays
// with perfect square sum
long countSubs = 0;
// As 0 is a perfect square,
// so we initialize 0th
// index-key with value 1
mp.Add(0, 1);
// Here we count the perfect
// square subarray sum by
// searching if there is a
// prefix with
// sum = (current prefixSum -
// (sq*sq))
for (int i = 0; i < n; i++)
{
for (int j = 0; prefixSum[i] - j *
j >= prefixMin; j++)
{
if (mp.ContainsKey(prefixSum[i] -
j * j))
// Increasing our subarray count
countSubs += mp[prefixSum[i] -
j * j];
}
// Increasing the current prefixSum
// index value in map by 1 to count
// the other perfect squares while
// traversing further
if(mp.ContainsKey(prefixSum[i]))
{
mp[prefixSum[i]]++;
}
else
{
mp.Add(prefixSum[i], 1);
}
}
return countSubs;
}
// Driver code
public static void Main(String[] args)
{
int []arr = {2, 3, -5,
6, -7, 4};
int n = arr.Length;
long ans = countSubarrays(arr, n);
// Printing the result
Console.Write(ans);
}
}
// This code is contributed by gauravrajput1
Javascript
<script>
// Javascript code for
// the above approach.
// Function to find count of
// subarrays whose sum is
// a perfect square.
function countSubarrays(arr, n)
{
// To search for index with
// (current prefix sum - j*j)
let mp = new Map();
// Storing the prefix sum
let prefixSum = Array.from({length: n}, (_, i) => 0);
// Used to track the minimum
// value in prefixSum
let prefixMin = 0;
prefixSum[0] = arr[0];
prefixMin = Math.min(prefixMin,
prefixSum[0]);
// Calculating the prefixSum
// and tracking the prefixMin
for (let i = 1; i < n; i++)
{
prefixSum[i] = prefixSum[i - 1] + arr[i];
// Below statement is used if
// array contains
// negative numbers
prefixMin = Math.min(prefixMin,
prefixSum[i]);
}
// Counts the no of subarrays
// with perfect square sum
let countSubs = 0;
// As 0 is a perfect square,
// so we initialize 0th
// index-key with value 1
mp.set(0, 1);
// Here we count the perfect
// square subarray sum by
// searching if there is a
// prefix with
// sum = (current prefixSum - (sq*sq))
for (let i = 0; i < n; i++)
{
for (let j = 0;
prefixSum[i] - j *
j >= prefixMin; j++)
{
if (mp.has(prefixSum[i] - j * j))
// Increasing our subarray count
countSubs += mp.get(prefixSum[i] -
j * j);
}
// Increasing the current prefixSum
// index value in map by 1 to count
// the other perfect squares while
// traversing further
if(mp.has(prefixSum[i]))
{
mp.set(prefixSum[i],
mp.get(prefixSum[i]) + 1);
}
else
{
mp.set(prefixSum[i], 1);
}
}
return countSubs;
}
// Driver code
let arr = [2, 3, -5,
6, -7, 4];
let n = arr.length;
let ans = countSubarrays(arr, n);
// Printing the result
document.write(ans);
// This code is contributed by souravghosh0416.
</script>
5
Complejidad de tiempo: O(N * sqrt(K))
Espacio auxiliar: O(N)
Publicación traducida automáticamente
Artículo escrito por Ankit Banerjee y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA