Recuento de rutas de raíz a hoja que consisten en como máximo M Nodes consecutivos que tienen valor K

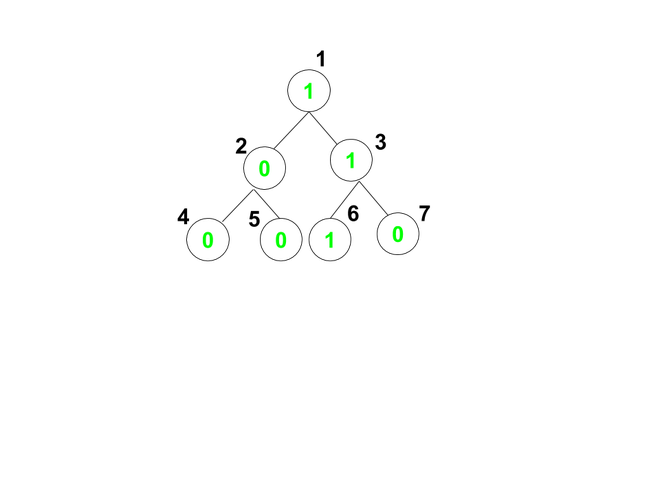
Dado un gráfico no dirigido acíclico en forma de árbol binario con la raíz en el vértice 1 y los valores en cada vértice [1, N] indicados por la array arr[] , la tarea es encontrar el número de rutas de la raíz a la hoja que contienen como máximo m Nodes consecutivos con valor K .

Ejemplo:

Entrada: arr[] = {1, 0, 1, 0, 0, 1, 0}, K = 1, M = 2 
 

Salida: 3 
Explicación: 
Ruta 1: 1 -> 2 -> 4 contiene un máximo de 1 K consecutivo 
Ruta 2: 1 -> 2 -> 5 contiene un máximo de 1 K consecutivo 
Ruta 3: 1 -> 3 -> 6 contiene un máximo de 3 K consecutivos 
Camino 4: 1 -> 3 -> 7 contiene un máximo de 2 K consecutivos 
Dado que el valor dado de M es 2, por lo tanto, hay 3 caminos que contienen como máximo 2 K consecutivos.

Entrada: arr[] = {2, 1, 3, 2, 1, 2, 1, 4, 3, 5, 2}, K = 2, M = 2 
 

            2
         /     \
        1       3
      /   \    /  \
     2     1  2    1
   /  \   / \
  4    3 5   2

Salida: 3  

Enfoque: 
el problema se puede resolver utilizando el enfoque de búsqueda primero en profundidad : 

• La primera búsqueda en profundidad se puede utilizar para recorrer todas las rutas desde el vértice raíz.
• Cada vez, si el valor en el Node actual es K , incremente el conteo .
• De lo contrario, establezca el recuento en 0 .
• Si el conteo excede M , entonces regrese.
• De lo contrario, atraviesa sus Nodes vecinos y repite los pasos anteriores.
• Finalmente, imprime el valor del conteo obtenido.

A continuación se muestra la implementación del enfoque anterior:

// C++ Program to implement
// the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Initialize the adjacency
// list and visited array
vector<int> adj[100005];
int visited[100005] = { 0 };
int ans = 0;
 
// Function to find the number of root to
// leaf paths that contain atmost m
// consecutive nodes with value k
void dfs(int node, int count, int m,
         int arr[], int k)
{
    // Mark the current node
    // as visited
    visited[node] = 1;
 
    // If value at current node is k
    if (arr[node - 1] == k) {
 
        // Increment counter
        count++;
    }
    else {
        count = 0;
    }
 
    // If count is greater than m
    // return from that path
    if (count > m) {
        return;
    }
 
    // Path is allowed if size of present node
    // becomes 0 i.e it has no child root and
    // no more than m consecutive 1's
    if (adj[node].size() == 1 && node != 1) {
        ans++;
    }
 
    for (auto x : adj[node]) {
        if (!visited[x]) {
            dfs(x, count, m, arr, k);
        }
    }
}
 
// Driver Code
int main()
{
    int arr[] = { 2, 1, 3, 2, 1, 2, 1 };
    int N = 7, K = 2, M = 2;
 
    // Designing the tree
    adj[1].push_back(2);
    adj[2].push_back(1);
 
    adj[1].push_back(3);
    adj[3].push_back(1);
 
    adj[2].push_back(4);
    adj[4].push_back(2);
 
    adj[2].push_back(5);
    adj[5].push_back(2);
 
    adj[3].push_back(6);
    adj[6].push_back(3);
 
    adj[3].push_back(7);
    adj[7].push_back(3);
 
    // Counter counts no.
    // of consecutive nodes
    int counter = 0;
 
    dfs(1, counter, M, arr, K);
 
    cout << ans << "\n";
    return 0;
}

// Java program to implement
// the above approach
import java.util.*;
 
class GFG{
 
// Initialize the adjacency
// list and visited array
@SuppressWarnings("unchecked")
static Vector<Integer> []adj = new Vector[100005];
static int []visited = new int[100005];
static int ans = 0;
 
// Function to find the number of root to
// leaf paths that contain atmost m
// consecutive nodes with value k
static void dfs(int node, int count, int m,
                int arr[], int k)
{
     
    // Mark the current node
    // as visited
    visited[node] = 1;
 
    // If value at current node is k
    if (arr[node - 1] == k)
    {
         
        // Increment counter
        count++;
    }
    else
    {
        count = 0;
    }
 
    // If count is greater than m
    // return from that path
    if (count > m)
    {
        return;
    }
 
    // Path is allowed if size of present node
    // becomes 0 i.e it has no child root and
    // no more than m consecutive 1's
    if (adj[node].size() == 1 && node != 1)
    {
        ans++;
    }
 
    for(int x : adj[node])
    {
        if (visited[x] == 0)
        {
            dfs(x, count, m, arr, k);
        }
    }
}
 
// Driver Code
public static void main(String[] args)
{
    int arr[] = { 2, 1, 3, 2, 1, 2, 1 };
    int N = 7, K = 2, M = 2;
     
    for(int i = 0; i < adj.length; i++)
        adj[i] = new Vector<Integer>();
         
    // Designing the tree
    adj[1].add(2);
    adj[2].add(1);
 
    adj[1].add(3);
    adj[3].add(1);
 
    adj[2].add(4);
    adj[4].add(2);
 
    adj[2].add(5);
    adj[5].add(2);
 
    adj[3].add(6);
    adj[6].add(3);
 
    adj[3].add(7);
    adj[7].add(3);
 
    // Counter counts no.
    // of consecutive nodes
    int counter = 0;
 
    dfs(1, counter, M, arr, K);
 
    System.out.print(ans + "\n");
}
}
 
// This code is contributed by 29AjayKumar

# Python3 Program to implement
# the above approach
 
# Initialize the adjacency
# list and visited array
adj = [[] for i in range(100005)]
visited = [ 0 for i in range(100005)]
ans = 0;
  
# Function to find the number of root to
# leaf paths that contain atmost m
# consecutive nodes with value k
def dfs(node, count, m, arr, k):
     
    global ans
     
    # Mark the current node
    # as visited
    visited[node] = 1;
  
    # If value at current
    # node is k
    if (arr[node - 1] == k):
  
        # Increment counter
        count += 1;
     
    else:
        count = 0;   
  
    # If count is greater than m
    # return from that path
    if (count > m):
        return;   
  
    # Path is allowed if size
    # of present node becomes 0
    # i.e it has no child root and
    # no more than m consecutive 1's
    if (len(adj[node]) == 1 and node != 1):
        ans += 1
     
    for x in adj[node]:       
        if (not visited[x]):
            dfs(x, count, m, arr, k);
 
# Driver code
if __name__ == "__main__":
         
    arr = [2, 1, 3, 2, 1, 2, 1]
    N = 7
    K = 2
    M = 2
  
    # Designing the tree
    adj[1].append(2);
    adj[2].append(1);
  
    adj[1].append(3);
    adj[3].append(1);
  
    adj[2].append(4);
    adj[4].append(2);
  
    adj[2].append(5);
    adj[5].append(2);
  
    adj[3].append(6);
    adj[6].append(3);
  
    adj[3].append(7);
    adj[7].append(3);
  
    # Counter counts no.
    # of consecutive nodes
    counter = 0;
  
    dfs(1, counter, M, arr, K);   
    print(ans)       
 
# This code is contributed by rutvik_56

// C# program to implement
// the above approach
using System;
using System.Collections.Generic;
 
class GFG{
 
// Initialize the adjacency
// list and visited array
static List<int> []adj = new List<int>[100005];
static int []visited = new int[100005];
static int ans = 0;
 
// Function to find the number of root to
// leaf paths that contain atmost m
// consecutive nodes with value k
static void dfs(int node, int count, int m,
                int []arr, int k)
{
     
    // Mark the current node
    // as visited
    visited[node] = 1;
 
    // If value at current node is k
    if (arr[node - 1] == k)
    {
         
        // Increment counter
        count++;
    }
    else
    {
        count = 0;
    }
 
    // If count is greater than m
    // return from that path
    if (count > m)
    {
        return;
    }
 
    // Path is allowed if size of present node
    // becomes 0 i.e it has no child root and
    // no more than m consecutive 1's
    if (adj[node].Count == 1 && node != 1)
    {
        ans++;
    }
 
    foreach(int x in adj[node])
    {
        if (visited[x] == 0)
        {
            dfs(x, count, m, arr, k);
        }
    }
}
 
// Driver Code
public static void Main(String[] args)
{
    int []arr = { 2, 1, 3, 2, 1, 2, 1 };
    int K = 2, M = 2;
     
    for(int i = 0; i < adj.Length; i++)
        adj[i] = new List<int>();
         
    // Designing the tree
    adj[1].Add(2);
    adj[2].Add(1);
 
    adj[1].Add(3);
    adj[3].Add(1);
 
    adj[2].Add(4);
    adj[4].Add(2);
 
    adj[2].Add(5);
    adj[5].Add(2);
 
    adj[3].Add(6);
    adj[6].Add(3);
 
    adj[3].Add(7);
    adj[7].Add(3);
 
    // Counter counts no.
    // of consecutive nodes
    int counter = 0;
 
    dfs(1, counter, M, arr, K);
 
    Console.Write(ans + "\n");
}
}
 
// This code is contributed by Amit Katiyar

<script>
    // Javascript Program to implement the above approach
     
    // Initialize the adjacency
    // list and visited array
    let adj = new Array(100005);
    let visited = new Array(100005);
    visited.fill(0);
    let ans = 0;
 
    // Function to find the number of root to
    // leaf paths that contain atmost m
    // consecutive nodes with value k
    function dfs(node, count, m, arr, k)
    {
 
        // Mark the current node
        // as visited
        visited[node] = 1;
 
        // If value at current node is k
        if (arr[node - 1] == k)
        {
 
            // Increment counter
            count++;
        }
        else
        {
            count = 0;
        }
 
        // If count is greater than m
        // return from that path
        if (count > m)
        {
            return;
        }
 
        // Path is allowed if size of present node
        // becomes 0 i.e it has no child root and
        // no more than m consecutive 1's
        if (adj[node].length == 1 && node != 1)
        {
            ans++;
        }
 
        for(let x = 0; x < adj[node].length; x++)
        {
            if (visited[adj[node][x]] == 0)
            {
                dfs(adj[node][x], count, m, arr, k);
            }
        }
    }
     
    let arr = [ 2, 1, 3, 2, 1, 2, 1 ];
    let K = 2, M = 2;
      
    for(let i = 0; i < adj.length; i++)
        adj[i] = [];
          
    // Designing the tree
    adj[1].push(2);
    adj[2].push(1);
  
    adj[1].push(3);
    adj[3].push(1);
  
    adj[2].push(4);
    adj[4].push(2);
  
    adj[2].push(5);
    adj[5].push(2);
  
    adj[3].push(6);
    adj[6].push(3);
  
    adj[3].push(7);
    adj[7].push(3);
  
    // Counter counts no.
    // of consecutive nodes
    let counter = 0;
  
    dfs(1, counter, M, arr, K);
  
    document.write(ans + "</br>");
 
</script>

4

Complejidad Temporal: O(V + E) 
Espacio Auxiliar: O(V)