Recuento de caminos palindrómicos positivos en una array dada

Dada una array N x M de enteros, la tarea es contar el número de ventajas palindrómicas en la array. 
 

Palindrómico plus se forma cuando una subfila palindrómica y una subcolumna palindrómica se cruzan en el elemento medio. 
 

Ejemplos: 
 

Entrada: array = [[1, 2, 1], [2, 3, 2], [3, 2, 1]] 
Salida: 1 
Explicación: 
Fila palindrómica de (1, 0) – > (1, 2) y Columna palindrómica (0, 1) -> (2, 1) forman un plus palindrómico.
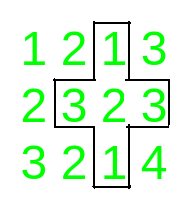
Entrada: array = [[1, 2, 1, 3], [2, 3, 2, 3], [3, 2, 1, 4] 
Salida: 2 
Explicación: 
Las ventajas palindrómicas en la array dada son: 
 

 

Enfoque: 
Para resolver el problema, siga los pasos a continuación: 
 

• Recorre todas las celdas que pueden ser el centro de un plus palindrómico, es decir, todas las celdas menos las que pertenecen a la primera y última fila y columnas.
• Para todas estas celdas (i, j) , verifique si a[i][j – 1] es igual a a[i][j + 1] y a[i – 1][j] es igual a a[i + 1][j] . Si se cumplen ambas condiciones, aumente el recuento de ventajas palindrómicas.
• Imprime el conteo final de pluses palindrómicos.

A continuación se muestra la implementación del enfoque anterior: 
 

// C++ Program to count the number
// of palindromic pluses in
// a given matrix
#include <bits/stdc++.h>
using namespace std;
 
// Function to count and return
// the number of palindromic pluses
int countPalindromicPlus(
    int n, int m,
    vector<vector<int> >& a)
{
    int i, j, k;
    int count = 0;
 
    // Traverse all the centers
    for (i = 1; i < n - 1; i++) {
        for (j = 1; j < m - 1; j++) {
 
            // Check for palindromic plus
            // Check whether row and
            // column are palindrome or not
            if (a[i + 1][j] == a[i - 1][j]
                && a[i][j - 1] == a[i][j + 1])
                ++count;
        }
    }
    // Return the answer
    return count;
}
 
// Driver code
int main()
{
    int n = 4, m = 4;
 
    vector<vector<int> > a
        = { { 1, 2, 1, 3 },
            { 2, 3, 2, 3 },
            { 3, 2, 1, 2 },
            { 2, 3, 2, 3 } };
    cout << countPalindromicPlus(
                n, m, a)
         << endl;
 
    return 0;
}

// Java program to count the number
// of palindromic pluses in
// a given matrix
class GFG{
 
// Function to count and return
// the number of palindromic pluses
static int countPalindromicPlus(int n, int m,
                                int [][]a)
{
    int i, j;
    int count = 0;
 
    // Traverse all the centers
    for(i = 1; i < n - 1; i++)
    {
       for(j = 1; j < m - 1; j++)
       {
           
          // Check for palindromic plus
          // Check whether row and
          // column are palindrome or not
          if (a[i + 1][j] == a[i - 1][j] &&
              a[i][j - 1] == a[i][j + 1])
              ++count;
       }
    }
     
    // Return the answer
    return count;
}
 
// Driver code
public static void main(String[] args)
{
    int n = 4, m = 4;
    int [][]a = { { 1, 2, 1, 3 },
                  { 2, 3, 2, 3 },
                  { 3, 2, 1, 2 },
                  { 2, 3, 2, 3 } };
                   
    System.out.print(
           countPalindromicPlus(n, m, a) + "\n");
}
}
 
// This code is contributed by amal kumar choubey

# Python3 Program to count the number
# of palindromic pluses in
# a given matrix
 
# Function to count and return
# the number of palindromic pluses
def countPalindromicPlus(n, m, a):
    i, j, k = 0, 0, 0
    count = 0
 
    # Traverse all the centers
    for i in range(1, n - 1):
        for j in range(1, m - 1):
 
            # Check for palindromic plus
            # Check whether row and
            # column are palindrome or not
            if (a[i + 1][j] == a[i - 1][j]
                and a[i][j - 1] == a[i][j + 1]):
                count += 1
                 
    # Return the answer
    return count
 
# Driver code
if __name__ == '__main__':
    n = 4
    m = 4
 
    a = [[1, 2, 1, 3 ],
         [2, 3, 2, 3 ],
         [3, 2, 1, 2 ],
         [2, 3, 2, 3 ]]
    print(countPalindromicPlus(n, m, a))
 
# This code is contributed by Mohit Kumar

// C# program to count the number
// of palindromic pluses in
// a given matrix
using System;
class GFG{
 
// Function to count and return
// the number of palindromic pluses
static int countPalindromicPlus(int n, int m,
                                int [,]a)
{
    int i, j;
    int count = 0;
 
    // Traverse all the centers
    for(i = 1; i < n - 1; i++)
    {
        for(j = 1; j < m - 1; j++)
        {
             
            // Check for palindromic plus
            // Check whether row and
            // column are palindrome or not
            if (a[i + 1, j] == a[i - 1, j] &&
                a[i, j - 1] == a[i, j + 1])
                ++count;
        }
    }
     
    // Return the answer
    return count;
}
 
// Driver code
public static void Main()
{
    int n = 4, m = 4;
    int [,]a = {{ 1, 2, 1, 3 },
                { 2, 3, 2, 3 },
                { 3, 2, 1, 2 },
                { 2, 3, 2, 3 }};
                 
    Console.Write(
            countPalindromicPlus(n, m, a) + "\n");
}
}
 
// This code is contributed by Code_Mech

<script>
 
    // JavaScript program to count the number
    // of palindromic pluses in a given matrix
     
    // Function to count and return
    // the number of palindromic pluses
    function countPalindromicPlus(n, m, a)
    {
        let i, j;
        let count = 0;
 
        // Traverse all the centers
        for(i = 1; i < n - 1; i++)
        {
           for(j = 1; j < m - 1; j++)
           {
 
              // Check for palindromic plus
              // Check whether row and
              // column are palindrome or not
              if (a[i + 1][j] == a[i - 1][j] &&
                  a[i][j - 1] == a[i][j + 1])
                  ++count;
           }
        }
 
        // Return the answer
        return count;
    }
     
    let n = 4, m = 4;
    let a = [ [ 1, 2, 1, 3 ],
               [ 2, 3, 2, 3 ],
               [ 3, 2, 1, 2 ],
               [ 2, 3, 2, 3 ] ];
                     
    document.write(countPalindromicPlus(n, m, a) + "</br>");
 
</script>

3

Complejidad de Tiempo: O(N ² ) 
Espacio Auxiliar: O(1)