Los investigadores de Uber Advanced Technologies Group propusieron la convolución de núcleo continuo paramétrico profundo. La motivación detrás de este documento es que la arquitectura simple de CNN asume una arquitectura similar a una cuadrícula y utiliza una convolución discreta como su bloque fundamental. Esto inhibe su capacidad para realizar una convolución precisa en muchas aplicaciones del mundo real. Por lo tanto, proponen un método de convolución llamado Convolución Continua Paramétrica.
Convolución continua paramétrica:
La convolución continua paramétrica es un operador de aprendizaje que opera sobre datos estructurados sin cuadrícula y explora núcleos parametrizados que abarcan un espacio vectorial continuo completo. Puede manejar estructuras de datos arbitrarias en la medida en que la estructura de soporte sea computable. El operador de convolución continuo se aproxima a un discreto por muestreo de Monte Carlo:
El siguiente desafío es definir g, que se parametriza de tal manera que a cada punto del dominio de soporte se le asigna un valor. Esto es imposible ya que requiere que g se defina sobre infinitos puntos de un dominio continuo.
Cuadrícula vs conversión continua
En su lugar, los autores utilizan el perceptrón multicapa como una función de convolución continua paramétrica aproximada porque son expresivos y capaces de aproximar las funciones continuas.
El kernel g(z,∅ ): R D → R se extiende sobre dominios de soporte continuo completo mientras permanece parametrizado por un número finito de cálculos
Capa de convolución continua paramétrica:
La capa de convolución continua paramétrica tiene 3 partes:
- Vector de características de entrada
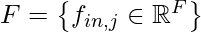
- Ubicación asociada en el dominio de soporte
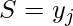
- Ubicación del dominio de salida
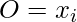
Para cada capa, primero evaluamos la función kernel:
; given parameter 
. Each element of the output vector can be calculated as:
donde, N es el número de puntos de entrada, M es el número de puntos de salida y D la dimensionalidad del dominio de soporte y F y O son las dimensiones de las características de entrada y salida predefinidas, respectivamente. Aquí, podemos observar la siguiente diferencia de la convolución discreta:
- La función kernel es una función continua dada la posición relativa en el dominio de soporte.
- Los puntos (de entrada, de salida) también pueden ser cualquier punto en el dominio continuo y pueden ser diferentes.
Arquitectura:
La red toma la característica de entrada y su posición asociada en el dominio de soporte como entrada. Siguiendo la arquitectura estándar de CNN, podemos agregar la normalización por lotes, las no linealidades y la conexión residual entre capas, lo cual fue fundamental para ayudar a la convergencia. La agrupación se puede emplear sobre el dominio de soporte para agregar información.
Arquitectura Deep Para CKConv
Convolución de cumplimiento de localidad
La convolución estándar calculada sobre un tamaño M de kernel limitado para imponer la localidad en los escenarios discretos. Sin embargo, la función continua puede imponer la localidad calculando la función que encuentra los puntos más cercanos a x.
Donde, w() es una función de ventana de modulación para hacer cumplir la localidad. Utiliza el k-vecino más cercano en su algoritmo.
Capacitación
Dado que todos los componentes básicos del modelo pueden ser diferenciables dentro de su dominio, podemos escribir la función de retropropagación como:
