Este artículo tiene como objetivo implementar una red neuronal profunda con un número arbitrario de capas ocultas, cada una de las cuales contiene un número diferente de neuronas. Implementaremos esta red neuronal utilizando algunas funciones auxiliares y, por último, combinaremos estas funciones para crear el modelo de red neuronal de capa L.
L: estructura de red neuronal profunda de capa (para comprender)
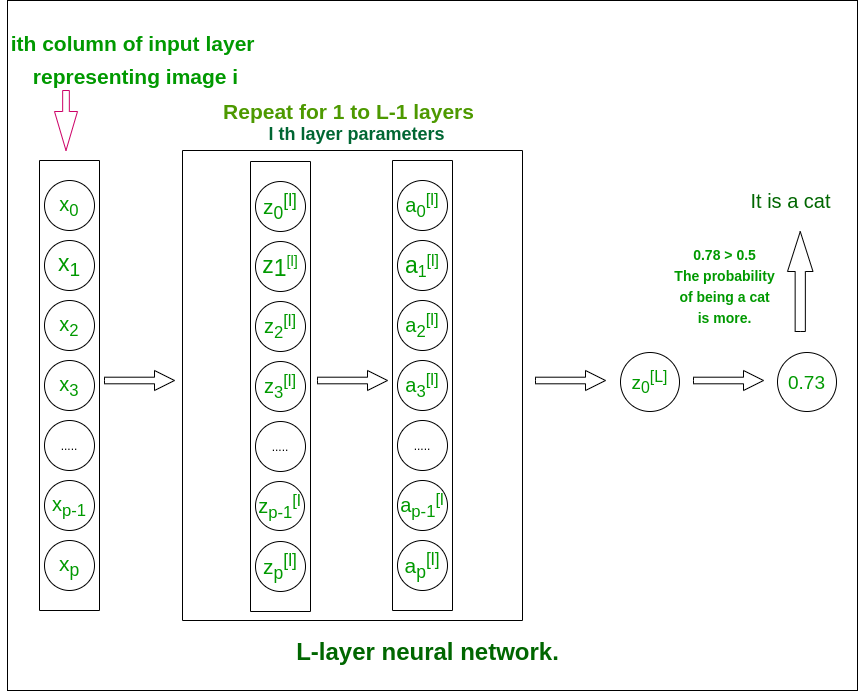
L – red neuronal de capa
La estructura del modelo es [LINEAL -> tanh](L-1 veces) -> LINEAL -> SIGMOID. es decir, tiene capas L-1 que utilizan la función de tangente hiperbólica como función de activación seguida de la capa de salida con una función de activación sigmoidea.
Más sobre funciones de activación
Implementación paso a paso de la red neuronal:
Initialize the parameters for the L layers Implement the forward propagation module Compute the loss at the final layer Implement the backward propagation module Finally, update the parameters Train the model using existing training dataset Use trained parameters to test model
Convenciones de nomenclatura seguidas en el artículo para evitar confusiones:
- Cada capa de la red está representada por un conjunto de dos parámetros array W (array de peso) y array b (array de polarización). Para la capa, i estos parámetros se representan como Wi y bi respectivamente.
- La salida lineal de la capa i se representa como Zi y la salida después de la activación se representa como Ai . Las dimensiones de Zi y Ai son las mismas.
Dimensiones de las arrays de pesos y sesgos.
La capa de entrada es del tamaño (x, m) donde m es el número de imágenes.
| Número de capa | Forma de W | forma de b | Salida lineal | Forma de activación |
|---|---|---|---|---|
| Capa 1 | ||||
| Capa 2 | ||||
| : | ||||
| Capa L – 1 | ||||
| Capa L |
Código: Importación de todas las bibliotecas de python requeridas.
Python3
import time import numpy as np import h5py import matplotlib.pyplot as plt import scipy from PIL import Image from scipy import ndimage
Inicialización:
- Usaremos inicialización aleatoria para las arrays de peso (para evitar resultados idénticos de todas las neuronas en la misma capa).
- Inicialización cero para los sesgos.
- El número de neuronas en cada capa se almacena en el diccionario layer_dims con claves como número de capa.
Código:
Python3
def initialize_parameters_deep(layer_dims):
# 0th layer is the input layer with number
# of columns stored in layer_dims.
parameters = {}
# number of layers in the network
L = len(layer_dims)
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layer_dims[l],
layer_dims[l - 1])*0.01
parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
return parameters
Módulo de propagación hacia adelante:
El módulo de propagación hacia adelante se completará en tres pasos. Completaremos tres funciones en este orden:
- linear_forward (para calcular la salida lineal Z para cualquier capa)
- linear_activation_forward donde la activación será tanh o Sigmoid.
- L_model_forward [LINEAR -> tanh](L-1 veces) -> LINEAL -> SIGMOID (modelo completo)
El módulo directo lineal (vectorizado sobre todos los ejemplos) calcula las siguientes ecuaciones:
Zi = Wi * A(i – 1) + bi Ai = activación_func(Zi)
Código:
Python3
def linear_forward(A_prev, W, b): # cache is stored to be used in backward propagation module Z = np.dot(W, A_prev) + b cache = (A, W, b) return Z, cache
Python3
def sigmoid(Z):
A = 1/(1 + np.exp(-Z))
return A, {'Z' : Z}
def tanh(Z):
A = np.tanh(Z)
return A, {'Z' : Z}
def linear_activation_forward(A_prev, W, b, activation):
# cache is stored to be used in backward propagation module
if activation == "sigmoid":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = sigmoid(Z)
elif activation == "tanh":
Z, linear_cache = linear_forward(A_prev, W, b)
A, activation_cache = tanh(Z)
cache = (linear_cache, activation_cache)
return A, cache
Python3
def L_model_forward(X, parameters): """ Arguments: X -- data, numpy array of shape (input size, number of examples) parameters -- output of initialize_parameters_deep() Returns: AL -- last post-activation value caches -- list of caches containing: every cache of linear_activation_forward() (there are L-1 of them, indexed from 0 to L-1) """ caches = [] A = X # number of layers in the neural network L = len(parameters) // 2 # Implement [LINEAR -> TANH]*(L-1). Add "cache" to the "caches" list. for l in range(1, L): A_prev = A A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], 'tanh') caches.append(cache) # Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list. AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], 'sigmoid') caches.append(cache) return AL, caches
![Rendered by QuickLaTeX.com \[ {\Huge J = \frac{1}{m}\sum_{i=1}^{\m}y^{(i)}log(a^{[L][i]}) + (1 - y^{(i)})log(1 - a^{[L][i]})} \]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-05c157509fd9584a69acf34dc608903c_l3.png)
Usaremos esta función de costo que medirá el costo de la capa de salida para todos los datos de entrenamiento.
Código:
Python3
def compute_cost(AL, Y): """ Implement the cost function defined by the equation. m = Y.shape[1] cost = (-1 / m)*(np.dot(np.log(AL), Y.T)+np.dot(np.log((1-AL)), (1 - Y).T)) # To make sure your cost's shape is what we # expect (e.g. this turns [[20]] into 20). cost = np.squeeze(cost) return cost
Módulo de propagación hacia atrás:
similar al módulo de propagación hacia adelante , también implementaremos tres funciones en este módulo.
- linear_backward (para calcular la salida lineal Z para cualquier capa)
- linear_activation_backward donde la activación será tanh o Sigmoid.
- L_model_backward [LINEAR -> tanh](L-1 veces) -> LINEAR -> SIGMOID (propagación hacia atrás del modelo completo)
Para la capa i, la parte lineal es: Zi = Wi * A(i – 1) + bi
Denotando dZi = ![]() podemos obtener dWi, dbi y dA(i – 1) como –
podemos obtener dWi, dbi y dA(i – 1) como – ![]()
![]()
![]()
Estas ecuaciones se formulan usando cálculo diferencial y manteniendo las dimensiones de arrays apropiadas para la multiplicación de puntos de array utilizando la función np.dot().
Código: código de Python para la implementación
Python3
def linear_backward(dZ, cache): A_prev, W, b = cache m = A_prev.shape[1] dW = (1 / m)*np.dot(dZ, A_prev.T) db = (1 / m)*np.sum(dZ, axis = 1, keepdims = True) dA_prev = np.dot(W.T, dZ) return dA_prev, dW, db
Aquí calcularemos la derivada de las funciones sigmoidea y tanh. Comprender la derivación de las funciones de activación
Código:
Python3
def sigmoid_backward(dA, activation_cache): Z = activation_cache['Z'] A = sigmoid(Z) return dA * (A*(1 - A)) # A*(1 - A) is the derivative of sigmoid function def tanh_backward(dA, activation_cache): Z = activation_cache['Z'] A = sigmoid(Z) return dA * (1 -np.power(A, 2)) # A*(1 -
L-model-backward:
recuerda que cuando implementaste la función L_model_forward, en cada iteración, almacenaste un caché que contiene (X, W, b y Z). En el módulo de retropropagación, utilizará esas variables para calcular los gradientes.
Python3
def L_model_backward(AL, Y, caches):
"""
AL -- probability vector, output of the forward propagation (L_model_forward())
Y -- true "label" vector (containing 0 if non-cat, 1 if cat)
caches -- list of caches containing:
every cache of linear_activation_forward() with "tanh"
(it's caches[l], for l in range(L-1) i.e l = 0...L-2)
the cache of linear_activation_forward() with "sigmoid"
(it's caches[L-1])
Returns:
grads -- A dictionary with the gradients
grads["dA" + str(l)] = ...
grads["dW" + str(l)] = ...
grads["db" + str(l)] = ...
"""
grads = {}
L = len(caches) # the number of layers
m = AL.shape[1]
Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL
# Initializing the backpropagation
# derivative of cost with respect to AL
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
# Lth layer (SIGMOID -> LINEAR) gradients. Inputs: "dAL, current_cache".
# Outputs: "grads["dAL-1"], grads["dWL"], grads["dbL"]
current_cache = caches[L - 1]
grads["dA" + str(L-1)], grads["dW" + str(L)], grads["db" + str(L)] = \
linear_activation_backward(dAL, current_cache, 'sigmoid')
# Loop from l = L-2 to l = 0
for l in reversed(range(L-1)):
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(
grads['dA' + str(l + 1)], current_cache, 'tanh')
grads["dA" + str(l)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
return grads
Parámetros de actualización:
Wi = Wi – a*dWi
bi = bi – a*dbi
(donde a es una constante apropiada conocida como tasa de aprendizaje)
Python3
def update_parameters(parameters, grads, learning_rate): L = len(parameters) // 2 # number of layers in the neural network # Update rule for each parameter. Use a for loop. for l in range(L): parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads['dW' + str(l + 1)] parameters["b" + str(l + 1)] = parameters['b' + str(l + 1)] - learning_rate * grads['db' + str(l + 1)] return parameters
Código: Entrenamiento del modelo
Ahora es el momento de acumular todas las funciones escritas antes para formar el modelo de red neuronal en capas L final. El argumento X en L_layer_model será el conjunto de datos de entrenamiento e Y serán las etiquetas correspondientes.
Python3
def L_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost = False):
"""
Arguments:
X -- data, numpy array of shape (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if cat, 1 if non-cat),
of shape (1, number of examples)
layers_dims -- list containing the input size and each layer size,
of length (number of layers + 1).
learning_rate -- learning rate of the gradient descent update rule
num_iterations -- number of iterations of the optimization loop
print_cost -- if True, it prints the cost every 100 steps
Returns:
parameters -- parameters learned by the model. They can then be used to predict.
"""
np.random.seed(1)
costs = [] # keep track of cost
parameters = initialize_parameters_deep(layers_dims)
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: [LINEAR -> TANH]*(L-1) -> LINEAR -> SIGMOID.
AL, caches = L_model_forward(X, parameters)
# Compute cost.
cost = compute_cost(AL, Y)
# Backward propagation.
grads = L_model_backward(AL, Y, caches)
# Update parameters.
parameters = update_parameters(parameters, grads, learning_rate)
# Print the cost every 100 training example
if print_cost and i % 100 == 0:
print ("Cost after iteration % i: % f" %(i, cost))
if print_cost and i % 100 == 0:
costs.append(cost)
# plot the cost
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
Código: implementar la función de predicción para probar la imagen proporcionada.
Python3
def predict(parameters, path_image):
my_image = path_image
image = np.array(ndimage.imread(my_image, flatten = False))
my_image = scipy.misc.imresize(image,
size =(num_px, num_px)).reshape((
num_px * num_px * 3, 1))
my_image = my_image / 255.
output, cache = L_model_forward(my_image, parameters)
output = np.squeeze(output)
prediction = round(output)
if(prediction == 1):
label = "Cat picture"
else:
label = "Non-Cat picture" # If the model is trained to recognize a cat image.
print ("y = " + str(prediction) + ", your L-layer model predicts a \"" + label)
Layers_dims proporcionados = [12288, 20, 7, 5, 1] cuando este modelo se entrena con una cantidad adecuada de conjuntos de datos de entrenamiento, tiene una precisión de hasta el 80 % en los datos de prueba.
Los parámetros se encuentran después del entrenamiento con una cantidad adecuada de conjuntos de datos de entrenamiento.
Python3
{'W1': array([[ 0.01672799, -0.00641608, -0.00338875, ..., -0.00685887,
-0.00593783, 0.01060475],
[ 0.01395808, 0.00407498, -0.0049068, ..., 0.01317046,
0.00221326, 0.00930175],
[-0.00123843, -0.00597204, 0.00472214, ..., 0.00101904,
-0.00862638, -0.00505112],
...,
[ 0.00140823, -0.00137711, 0.0163992, ..., -0.00846451,
-0.00761603, -0.00149162],
[-0.00168698, -0.00618577, -0.01023935, ..., 0.02050705,
-0.00428185, 0.00149319],
[-0.01770891, -0.0067836, 0.00756873, ..., 0.01730701,
0.01297081, -0.00322241]]), 'b1': array([[ 3.85542520e-03],
[ 8.18087056e-03],
[ 6.52138546e-03],
[ 2.85633678e-03],
[ 6.01081275e-03],
[ 8.17122684e-04],
[ 3.72986493e-04],
[ 7.05992009e-04],
[ 4.36344692e-04],
[ 1.90827285e-03],
[ -6.51686461e-03],
[ 6.97258125e-03],
[ -1.08988113e-03],
[ 5.40858776e-03],
[ 8.16752511e-03],
[ -1.05298871e-02],
[ -9.05267219e-05],
[ -5.13240993e-04],
[ 1.42355924e-03],
[ -2.40912130e-03]]), 'W2': array([[ 2.02109232e-01, -3.08645240e-01, -3.77620591e-01,
-4.02563039e-02, 5.90753267e-02, 1.23345558e-01,
3.08047246e-01, 4.71201576e-02, 5.29892230e-02,
1.34732883e-01, 2.15804697e-01, -6.34295948e-01,
-1.56081006e-01, 1.01905466e-01, -1.50584386e-01,
5.31219819e-02, 1.14257132e-01, 4.20697960e-01,
1.08551174e-01, -2.18735332e-01],
[ 3.57091131e-01, -1.40997155e-01, 3.70857247e-01,
2.53207014e-01, -1.12596978e-01, -3.15179195e-01,
-2.48100731e-01, 4.72723584e-01, -7.71870940e-02,
5.39834663e-01, -1.17927181e-02, 6.45463019e-02,
2.73704423e-02, 4.30157714e-01, 1.59318390e-01,
-6.48089126e-01, -1.71894333e-01, 1.77933527e-01,
1.54736463e-01, -7.26815274e-02],
[ 2.96501527e-01, 2.43056424e-01, -1.22400000e-02,
2.69275366e-02, 3.76041647e-01, -1.70245407e-01,
-2.95343754e-02, -7.35716150e-02, -1.80179693e-01,
-5.77515859e-03, -6.38323383e-01, 6.94950669e-02,
7.66137263e-02, 3.66599261e-01, 5.40904716e-02,
-1.51814996e-01, -2.61672559e-01, 1.35946854e-01,
4.21086332e-01, -2.71073484e-01],
[ 1.42186042e-01, -2.66789439e-01, 4.57188131e-01,
2.84732743e-02, -5.49143391e-02, -3.96786581e-02,
-1.68668726e-01, -1.46525541e-01, 3.25325993e-03,
-1.13045329e-01, 4.03935681e-01, -3.92214264e-01,
5.25325051e-04, -3.69642647e-01, -1.15812921e-01,
1.32695899e-01, 3.20810624e-01, 1.88127350e-01,
-4.82784806e-02, -1.48816756e-01],
[ -1.65469406e-01, 4.24741323e-01, -5.76900900e-01,
1.58084434e-01, -2.90965849e-01, 3.40124014e-02,
-2.62189635e-01, 2.66917709e-01, 4.77530579e-01,
-1.73491365e-01, -1.48434710e-01, -6.91270097e-02,
5.42923817e-03, -2.85173244e-01, 6.40701002e-02,
-7.33126171e-02, 1.43543481e-01, 7.82250247e-02,
-1.47535352e-01, -3.99073661e-01],
[ -2.05468389e-01, 1.66914752e-01, 2.15918881e-01,
2.21774761e-01, 2.52527888e-01, 2.64464223e-01,
-3.07796263e-02, -3.06999665e-01, 3.45835418e-01,
1.05973413e-01, -3.47687682e-01, 9.13383273e-02,
3.97150339e-02, -3.14285982e-01, 2.22363710e-01,
-3.93921988e-01, -9.70224337e-02, -3.03701358e-01,
1.40075127e-01, -4.56621577e-01],
[ 2.06819296e-01, -2.39537245e-01, -4.06133490e-01,
5.92692802e-02, 8.95374287e-02, -3.27700300e-01,
-6.89856027e-02, -6.13447906e-01, 1.89927573e-01,
-1.42814095e-01, 1.77958823e-03, -1.34407806e-01,
9.34036862e-02, -2.00549616e-02, 9.01789763e-02,
3.81627943e-01, 3.30416268e-01, -1.76566228e-02,
9.28388267e-02, -1.16167106e-01]]), 'b2': array([[-0.00088887],
[ 0.02357712],
[ 0.01858614],
[-0.00567557],
[ 0.00636179],
[ 0.02362429],
[-0.00173074]]), 'W3': array([[ 0.20939786, 0.21977478, 0.77135171, -1.07520777, -0.64307173,
-0.24097649, -0.15626735],
[-0.57997618, 0.30851841, -0.03802324, -0.13489975, 0.23488207,
0.76248961, -0.34515092],
[ 0.15990295, 0.5163969, 0.15284381, 0.42790606, -0.05980168,
0.87865156, -0.01031899],
[ 0.52908282, 0.93882471, 1.23044256, -0.01481286, 0.41024244,
0.18731983, -0.01414658],
[-0.96753783, -0.30492002, 0.54060558, -0.18776932, -0.39245146,
0.20654634, -0.58863038]]), 'b3': array([[ 0.8623361 ],
[-0.00826002],
[-0.01151116],
[-0.06844291],
[-0.00833715]]), 'W4': array([[-0.83045967, 0.18418824, 0.85885352, 1.41024115, 0.12713131]]), 'b4': array([[-1.73123633]])}
Probar una imagen personalizada

Python3
my_image = "https://www.pexels.com / photo / adorable-animal-blur-cat-617278/" predict(parameters, my_image)
Salida con parámetros aprendidos:
y = 1, your L-layer model predicts a Cat picture.
Publicación traducida automáticamente
Artículo escrito por hackerblack1004 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA