Requisitos previos: redes neuronales recurrentes, redes de memoria a largo plazo
Para resolver el problema de los gradientes de desaparición-explosión que a menudo se encuentra durante el funcionamiento de una red neuronal recurrente básica, se desarrollaron muchas variaciones. Una de las variaciones más famosas es la Red de Memoria a Largo Corto Plazo (LSTM) . Una de las variaciones menos conocidas pero igualmente efectivas es Gated Recurrent Unit Network (GRU) .
A diferencia de LSTM, consta de solo tres puertas y no mantiene un estado de celda interno. La información que se almacena en el estado de celda interno en una unidad recurrente LSTM se incorpora al estado oculto de la unidad recurrente cerrada. Esta información colectiva se pasa a la siguiente Unidad Recurrente Cerrada. Las diferentes puertas de una GRU se describen a continuación:
- Actualizar puerta (z): determina cuánto del conocimiento pasado debe transmitirse al futuro. Es análogo a la puerta de salida en una unidad recurrente LSTM.
- Reset Gate(r): Determina cuánto del conocimiento pasado se debe olvidar. Es análogo a la combinación de Input Gate y Forget Gate en una unidad recurrente LSTM.
- Puerta de memoria actual (
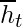 ): a menudo se pasa por alto durante una discusión típica sobre la red de unidades recurrentes cerradas. Se incorpora a la puerta de reinicio al igual que la puerta de modulación de entrada es una subparte de la puerta de entrada y se utiliza para introducir algo de no linealidad en la entrada y también para hacer que la entrada sea de media cero. Otra razón para convertirlo en una subparte de la puerta de reinicio es reducir el efecto que tiene la información anterior sobre la información actual que se transmite al futuro.
): a menudo se pasa por alto durante una discusión típica sobre la red de unidades recurrentes cerradas. Se incorpora a la puerta de reinicio al igual que la puerta de modulación de entrada es una subparte de la puerta de entrada y se utiliza para introducir algo de no linealidad en la entrada y también para hacer que la entrada sea de media cero. Otra razón para convertirlo en una subparte de la puerta de reinicio es reducir el efecto que tiene la información anterior sobre la información actual que se transmite al futuro.
El flujo de trabajo básico de una red de unidades recurrentes cerrada es similar al de una red neuronal recurrente básica cuando se ilustra, la principal diferencia entre los dos está en el funcionamiento interno dentro de cada unidad recurrente, ya que las redes de unidades recurrentes cerradas consisten en puertas que modulan el entrada actual y el estado oculto anterior.

Funcionamiento de una Unidad Recurrente Cerrada:
- Tome la entrada actual y el estado oculto anterior como vectores.
- Calcule los valores de las tres puertas diferentes siguiendo los pasos que se detallan a continuación:
- Para cada puerta, calcule la entrada actual parametrizada y los vectores de estado previamente ocultos realizando una multiplicación por elementos (producto de Hadamard) entre el vector en cuestión y los pesos respectivos para cada puerta.
- Aplique la función de activación respectiva para cada elemento de puerta en los vectores parametrizados. A continuación se muestra la lista de las puertas con la función de activación que se aplicará a la puerta.
Update Gate : Sigmoid Function Reset Gate : Sigmoid Function
- El proceso de cálculo de la puerta de memoria actual es un poco diferente. Primero, se calcula el producto de Hadamard de Reset Gate y el vector de estado previamente oculto. Luego, este vector se parametriza y luego se agrega al vector de entrada actual parametrizado.
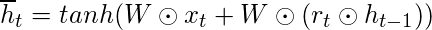
- Para calcular el estado oculto actual, primero se define un vector de unos y las mismas dimensiones que el de la entrada. Este vector se llamará unos y se denotará matemáticamente por 1. Primero, calcule el Producto de Hadamard de la puerta de actualización y el vector de estado previamente oculto. Luego genere un nuevo vector restando la puerta de actualización de unos y luego calcule el Producto de Hadamard del vector recién generado con la puerta de memoria actual. Finalmente, agregue los dos vectores para obtener el vector de estado actualmente oculto.

El trabajo mencionado anteriormente se establece a continuación: –

Tenga en cuenta que los círculos azules indican la multiplicación por elementos. El signo positivo en el círculo denota la suma de vectores, mientras que el signo negativo denota la resta de vectores (suma de vectores con valor negativo). La array de peso W contiene diferentes pesos para el vector de entrada actual y el estado oculto anterior para cada puerta.
Al igual que las redes neuronales recurrentes, una red GRU también genera una salida en cada paso de tiempo y esta salida se usa para entrenar la red mediante el descenso de gradiente.

Tenga en cuenta que, al igual que el flujo de trabajo, el proceso de capacitación para una red GRU también es similar en diagrama al de una red neuronal recurrente básica y difiere solo en el funcionamiento interno de cada unidad recurrente.
El algoritmo de retropropagación a través del tiempo para una red de unidades recurrentes cerradas es similar al de una red de memoria a largo plazo y difiere solo en la formación de la string diferencial.
Sea ![]() la salida predicha en cada paso de tiempo y
la salida predicha en cada paso de tiempo y ![]() sea la salida real en cada paso de tiempo. Entonces el error en cada paso de tiempo está dado por: –
sea la salida real en cada paso de tiempo. Entonces el error en cada paso de tiempo está dado por: –
![]()
El error total viene dado por la suma de errores en todos los pasos de tiempo.
![]()
![]()
De manera similar, el valor ![]() se puede calcular como la suma de los gradientes en cada paso de tiempo.
se puede calcular como la suma de los gradientes en cada paso de tiempo.
![]()
Usando la regla de la string y usando el hecho de que ![]() es una función de
es una función de ![]() y que de hecho es una función de
y que de hecho es una función de ![]() , surge la siguiente expresión:
, surge la siguiente expresión:
![]()
Por lo tanto, el gradiente de error total viene dado por lo siguiente:
![]()
Tenga en cuenta que la ecuación de gradiente involucra una string ![]() que se parece a la de una red neuronal recurrente básica, pero esta ecuación funciona de manera diferente debido al funcionamiento interno de los derivados de
que se parece a la de una red neuronal recurrente básica, pero esta ecuación funciona de manera diferente debido al funcionamiento interno de los derivados de ![]() .
.
¿Cómo resuelven las Unidades Recurrentes Cerradas el problema de los gradientes que se desvanecen?
El valor de los gradientes está controlado por la string de derivadas a partir de ![]() . Recuerde la expresión para
. Recuerde la expresión para ![]() :-
:-
![]()
Usando la expresión anterior, el valor de ![]() es: –
es: –
![]()
Recuerde la expresión para ![]() :-
:-
![]()
Usando la expresión anterior para calcular el valor de ![]() : –
: –
![]()
Dado que tanto la puerta de actualización como la de reinicio utilizan la función sigmoide como su función de activación, ambas pueden tomar valores de 0 o 1.
Caso 1(z = 1):
En este caso, independientemente del valor de ![]() , el término
, el término ![]() es igual a z que a su vez es igual a 1.
es igual a z que a su vez es igual a 1.
Caso 2A(z=0 y r=0):
En este caso, el término ![]() es igual a 0.
es igual a 0.
Caso 2B(z=0 y r=1):
En este caso, el término ![]() es igual a
es igual a ![]() . Este valor está controlado por la array de peso que se puede entrenar y, por lo tanto, la red aprende a ajustar los pesos de tal manera que el término
. Este valor está controlado por la array de peso que se puede entrenar y, por lo tanto, la red aprende a ajustar los pesos de tal manera que el término ![]() se acerque a 1.
se acerque a 1.
Así, el algoritmo Back-Propagation Through Time ajusta los pesos respectivos de tal manera que el valor de la string de derivadas sea lo más cercano posible a 1.
Publicación traducida automáticamente
Artículo escrito por AlindGupta y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA