Las redes neuronales autoasociativas son los tipos de redes neuronales cuyos vectores de entrada y salida son idénticos. Estos son tipos especiales de redes neuronales que se utilizan para simular y explorar el proceso asociativo. La asociación en esta arquitectura proviene de la instrucción de un conjunto de elementos de procesamiento simples llamados unidades que se conectan a través de conexiones ponderadas.
En estas redes, realizamos un entrenamiento para almacenar el vector ya sea bipolar o binario. Un vector almacenado se puede recuperar de un vector distorsionado o ruidoso si la entrada es similar.
Arquitectura
AANN contiene una red de avance de perceptrón de cinco capas, que se puede dividir en dos redes neuronales de 3 capas cada una conectada en serie (similar a la arquitectura de autocodificador). La red consta de una capa de entrada seguida de una capa oculta y una capa de cuello de botella. Esta capa de cuello de botella es común entre la red y un componente clave de la red. Proporciona compresión de datos a la entrada y la topología con potentes capacidades de extracción de características. A la capa de cuello de botella le sigue una segunda capa oculta no lineal y la capa de salida de la segunda red.

Arquitectura NN autoasociativa
La primera red comprime la información del vector n-dimensional a vectores de menor dimensión que contienen un menor número de variables características y representan todo el proceso. La segunda red funciona de forma opuesta a la primera y utiliza información comprimida para regenerar las n medidas redundantes originales.
Algoritmo
Usaremos la regla de Hebb en el algoritmo para establecer pesos porque los vectores de entrada y salida están perfectamente correlacionados, ya que la entrada y la salida tienen el mismo número de unidades de salida y de entrada.
Regla de Hebb:
- cuando A y B están positivamente correlacionados, aumente la fuerza de la conexión entre ellos.
- cuando A y B están correlacionados negativamente, entonces disminuye la fuerza de la conexión entre ellos.
- En la práctica, usamos la siguiente fórmula para establecer los pesos:
![]()
- donde, W = array ponderada
- T= Tasa de aprendizaje
- S(p) : patrones prototipo n-dimensionales p-distintos
Algoritmo de entrenamiento
- Inicialice todos los pesos para i= 1,2,3 …n y j= 1,2,3 …n tal que: w ij =0 .
- Para cada vector a almacenar, repita los siguientes pasos:
- Configure la activación para cada unidad de entrada i= 1 a n: x i = s i .
- Configure la activación para cada unidad de salida j = 1 a n: y j = s j .
- Actualice los pesos para i= 1,2,3 …n y j= 1,2,3 …n tal que: w ij (nuevo) = w ij (antiguo) + x i y j
Algoritmo de prueba/inferencia:
Para probar si la entrada es ‘conocida’ y ‘desconocida’ para el modelo, debemos realizar los siguientes pasos:
- Tome los pesos que se generaron durante la fase de entrenamiento utilizando la regla de Hebb.
- Para cada vector de entrada, realice los siguientes pasos:
- Establezca la activación en las unidades de entrada iguales a los vectores de entrada.
- Configurar la activación en unidades de salida para j= 1,2,3 …n:
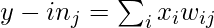
- Aplicar la función de activación para j= 1, 2, 3 … n:
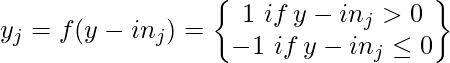
AANN reconoce el vector de entrada para ser conocido si la unidad de salida después de la activación generó el mismo patrón que uno almacenado en ella.
Capacidad de almacenamiento
- Una de las características importantes de AANN es la cantidad de patrones que se pueden almacenar antes de que la red comience a olvidar.
- El número de vectores que se pueden almacenar en la red se denomina capacidad de la red.
- La capacidad de los vectores depende de la relación entre ellos, es decir, se pueden almacenar más vectores si son mutuamente ortogonales. Generalmente, se pueden almacenar n-1 vectores mutuamente ortogonales con n componentes.
Aplicaciones
Las redes neuronales autoasociativas se pueden utilizar en muchos campos:
- Reconocimiento de patrones
- Bioinformática
- Reconocimiento de voz
- Validación de señal, etc.