Redes y gráficos de minería de datos

La minería de datos es el proceso de recopilar y procesar datos de un montón de datos sin procesar. Cuando se establecen los patrones, se pueden identificar varias relaciones entre los conjuntos de datos y se pueden presentar en un formato resumido que ayuda en el análisis estadístico en varias industrias. Entre las otras estructuras de datos, el gráfico se usa ampliamente en el modelado de estructuras y patrones avanzados. En minería de datos, el gráfico se usa para encontrar patrones de subgráficos para discriminación, clasificación, agrupación de datos, etc. El gráfico se usa en análisis de redes. Al vincular los diversos Nodes, los gráficos forman comunicaciones similares a redes, redes web y de computadoras, redes sociales, etc. En la minería de datos multirelacional, se utilizan gráficos o redes debido a la variada relación interconectada entre los conjuntos de datos en una base de datos relacional. 

Minería de grafos

La minería de gráficos es un proceso en el que las técnicas de minería se utilizan para encontrar un patrón o una relación en la colección dada de gráficos del mundo real. Al extraer el gráfico, se pueden identificar subestructuras y relaciones frecuentes que ayudan a agrupar los conjuntos de gráficos, encontrar una relación entre conjuntos de gráficos o discriminar o caracterizar gráficos. Predecir estas tendencias de patrones puede ayudar a crear modelos para mejorar cualquier aplicación que se utilice en tiempo real. Para implementar el proceso de minería de gráficos, uno debe aprender a extraer subgráficos frecuentes.

Minería de subgráficos frecuentes 

Consideremos un gráfico h con un conjunto de aristas E(h) y un conjunto de vértices V(h). Consideremos la existencia de isomorfismo de subgrafo de h a h’ de tal manera que h es un subgrafo de h’. Una función de etiqueta es una función que traza los bordes o los vértices de una etiqueta. Consideremos un conjunto de datos de gráficos etiquetados  . Consideremos s (h) como el soporte, lo que significa el porcentaje de gráficos en F donde h es un subgráfico. Un gráfico frecuente tiene un soporte que no será inferior al umbral mínimo de soporte. Indiquémoslo como min_support.

Pasos para encontrar subgrafos frecuentes:

Hay dos pasos para encontrar subgrafos frecuentes. 

• El primer paso es crear candidatos de subestructura frecuentes.
• El segundo paso es encontrar el apoyo de todos y cada uno de los candidatos. Debemos optimizar y mejorar el primer paso porque el segundo paso es un conjunto completo NP donde la complejidad computacional es precisa y alta.

Existen dos métodos para la extracción frecuente de subestructuras.

El enfoque basado en Apriori: El enfoque para encontrar los gráficos frecuentes comienza desde el gráfico con un tamaño pequeño. El enfoque avanza de abajo hacia arriba mediante la creación de candidatos con vértice o borde adicional. Este algoritmo se llama Gráfico A priori . Consideremos Q _kcomo el conjunto subestructura frecuente con un tamaño de k. Este enfoque adquiere una técnica de minería nivelada. Previamente a la técnica de Gráfico A priori, se debe realizar la generación de candidatos. Esto se hace combinando dos subgrafos frecuentes iguales pero ligeramente variados. Después de la formación de nuevas subestructuras, se verifica la frecuencia del gráfico. Fuera de eso, los gráficos que se encuentran con frecuencia se utilizan para crear el próximo candidato. Este paso para generar candidatos de subestructura frecuentes es un paso complejo. Pero, cuando se trata de generar candidatos en un conjunto de elementos, es fácil y sin esfuerzo. Consideremos un ejemplo de tener dos conjuntos de elementos de tamaño tres tales que   y   Por lo tanto, el conjunto de elementos derivado mediante la unión sería pqrs. Pero cuando se trata de subestructuras, hay más de un método para unir dos subestructuras.

Algoritmo: 

Este enfoque se basa en la extracción frecuente de subestructuras.

Input:
F= a graph data set.
min_support= minimum support threshold
Output:
Q1,Q2,Q3,....QK,
 a frequent substructure set graphs with the size range from 1 to k.
Q1 <- all the frequent 1 subgraphs in F;
k <- 2;
while Qk-1 ≠ ∅ do
 Qk <- ∅;
 Gk <- candidate_generation(Qk-1);
 foreach candidate l ∈ Gk do
  l.count <- 0;
  foreach Fi ∈ F do
    if isomerism_subgraph(l,Fi) then
    l.count <- l.count+1;
    end
  end
  if l.count ≥ min_support(F) ∧ l∉Qk then
     Qk = Qk U l;
  end
 end
 k <- k+1;
end

Es un método iterativo en el que tiene lugar la generación del primer candidato seguida del cálculo del soporte. Los subgrafos se generan usando isomorfismo de subgrafos. Por lo tanto, se generan subgrafos frecuentes mediante el uso eficiente de este enfoque que ayuda en FSM. El enfoque a priori utiliza BFS (Búsqueda primero en amplitud) debido a la generación iterativa de candidatos por niveles. Esto es necesario porque si desea extraer el gráfico k+1, ya debería haber extraído hasta k subgráficos.   

El enfoque de patrón de crecimiento: este enfoque de patrón de crecimiento puede usar tanto BFS como DFS (búsqueda primero en profundidad). Se prefiere DFS para este enfoque debido a su naturaleza de menor consumo de memoria. Consideremos un gráfico h. Se puede formar un nuevo gráfico agregando un borde e. La arista puede introducir un vértice pero no es una necesidad. Si introduce un vértice, se puede hacer de dos formas, hacia delante y hacia atrás. El gráfico de patrón de crecimiento es fácil pero no es tan eficiente. Porque existe la posibilidad de crear un gráfico similar que ya está creado, lo que conduce a la ineficiencia de cálculo. Los gráficos duplicados generados se pueden eliminar, pero aumenta el tiempo y el trabajo. Para evitar la creación de gráficos duplicados, los gráficos frecuentes deben introducirse con mucho cuidado y de forma conservadora, lo que exige la necesidad de otros algoritmos. 

Algoritmo:

El siguiente algoritmo es una minería de subestructura frecuente basada en patrones de crecimiento con un enfoque simplista. Si necesita buscar sin duplicar, debe usar un algoritmo diferente con gSpan.

Input:
q= a frequent graph
F= a graph data set.
min_support= minimum support threshold
Output: 
P = the frequent graph set
P <- ∅;
Call patterngrow_graph(q, F, min_support, P);
procedure patterngrow_graph(q, F, min_support, P)
 if q ∈ P then return;
 else insert q into P;
 scan F once, find all the edges e such that q can be extended to q -> e;
 for each frequent q -> e do
 PatternGrowthGraph(q -> e, D, min_support, P);
 return;

Una arista e se usa para extender un nuevo gráfico a partir del anterior q. El gráfico recién extendido se denota como   La extensión puede ser hacia atrás o hacia adelante. 

Minería de subestructuras basada en restricciones

De acuerdo con la solicitud del usuario, las restricciones describieron cambios en el proceso de minería. Pero, si los generalizamos y categorizamos en restricciones específicas, el proceso de minería se manejaría fácilmente empujándolos dentro de los marcos dados. La estrategia de empuje de restricciones se utiliza en tareas de minería de crecimiento de patrones. Veamos algunas categorías de restricciones importantes.

• Restricción de contención de subgráficos: cuando un usuario solicita un patrón con subgráficos específicos, se utiliza esta restricción. Esta restricción también se denomina restricción de contención establecida. El conjunto dado de subgráficos se toma como una consulta y luego la extracción se realiza en función de los datos elegidos al extender los patrones de los conjuntos de subgráficos. Esta técnica se puede utilizar para minar cuando el usuario solicita patrones con conjuntos específicos de aristas o vértices.
• Restricción de suma de valores: aquí, la restricción es la suma de los pesos en los bordes. Hay dos rangos alto y bajo. Las dos restricciones se designan como  y 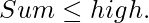  La primera condición se llama restricción monótona porque una vez que se cumple la condición, la extensión puede tener lugar agregando aristas hasta que se cumpla la siguiente condición. Pero la última condición se llama restricción antimonotónica porque una vez que se cumple la condición, no se puede hacer más extensión. Con este método, la técnica de imponer restricciones funcionará bien.
• Restricción geométrica : en esta restricción, se toma el ángulo entre un par de bordes dentro de un rango dado que está conectado. Consideremos un grafo h, tal que 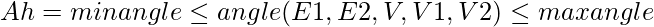 donde E ₁ , E ₂ son las aristas conectadas en el vértice V y conectadas a los otros dos vértices en los otros dos extremos V ₁ , V ₂ . A _h se denomina restricción antimonotónica porque si alguno de los ángulos formados al combinar dos aristas no satisface, no pasa al siguiente nivel y nunca cumplirá A _h . Puede llevarse al proceso de extensión de borde y eliminar cualquier extensión que no satisfaga A _h .

Análisis de red

En el concepto de análisis de redes, la relación entre las unidades se llama enlaces en un gráfico. Desde la perspectiva de la minería de datos, esto se denomina minería de enlaces o análisis de enlaces. La red es un conjunto de datos divergentes con un concepto multirelacional en forma de gráfico. El gráfico es muy grande con Nodes como objetos, bordes como enlaces que a su vez denotan la relación entre los Nodes u objetos. Los sistemas de redes telefónicas, WWW (World Wide Web) son muy buenos ejemplos. También ayuda a filtrar los conjuntos de datos y proporcionar servicios preferidos por el cliente. Cada red consta de numerosos Nodes. Los conjuntos de datos son ampliamente enormes. Por lo tanto, estudiar y extraer información útil de un amplio grupo de conjuntos de datos ayudaría a resolver problemas y transmitir datos de manera efectiva.

Minería de enlaces

Existen algunos métodos convencionales de aprendizaje automático en los que se toman objetos homogéneos de una relación. Pero en las redes, esto no es aplicable debido a la gran cantidad de Nodes y su naturaleza multirelacional y heterogénea. Así, la minería de enlaces ha aparecido como un nuevo campo después de muchos tipos de investigación. La minería de enlaces es la convergencia de múltiples investigaciones realizadas en minería de gráficos, redes, hipertextos, programación lógica, análisis de enlaces, análisis predictivo y modelado. Los enlaces no son más que la relación entre los Nodes de una red. Con la ayuda de enlaces, el proceso de minería se puede llevar a cabo de manera eficiente. Esto requiere que se realicen las diversas funciones. 

• Clasificación de objetos basada en enlaces: en la minería de enlaces, solo los atributos no son suficientes. Aquí también son necesarios los vínculos y las características de los Nodes vinculados. Un mejor ejemplo es la clasificación basada en la Web. En la clasificación basada en web, el sistema predice la categorización de una página web en función de la presencia de esa palabra específica, lo que significa que la palabra buscada aparece en esa página. El texto de anclaje es el que la persona hace clic en el hipervínculo que se abre durante la búsqueda. Estas dos cosas actúan como atributos en la clasificación basada en web. Los atributos pueden ser cualquier cosa que se relacione con el enlace y las páginas de red.
• Predicción del tipo de enlace: De acuerdo a los recursos del objeto involucrado, el sistema predice el motivo de ese enlace. En las organizaciones, ayuda a sugerir sesiones de comunicación interactiva entre los empleados si es necesario. En el mercado minorista en línea, ayuda a predecir lo que un cliente prefiere comprar, lo que puede aumentar las ventas y las recomendaciones.
• Predicción del tipo de objeto: aquí la predicción se basa en el tipo de objeto involucrado, sus atributos y propiedades, vínculos y rasgos del objeto vinculado a él. Por ejemplo, en el dominio del restaurante, se realiza un método similar para predecir si un cliente prefiere pedir comida o visitar directamente el restaurante. También ayuda a predecir el método de comunicación que prefiere un cliente, ya sea por teléfono o por correo.
• Enlace Estimación de Cardinalidad: En esta tarea, hay dos tipos de estimación. El primero es predecir el número de enlaces vinculados a un objeto. Por ejemplo, el porcentaje de autoridad de una página web se puede calcular encontrando la cantidad de enlaces vinculados a ella, lo que se denomina enlaces internos. Las páginas web que actúan como un centro, lo que significa que un conjunto de páginas web denota otros enlaces que pertenecen al mismo tema se pueden identificar mediante enlaces externos. Por ejemplo, cuando ocurre una pandemia, encontrar los vínculos del paciente afectado puede llevarnos a los otros pacientes, lo que ayuda a controlar la transmisión. El segundo se realiza prediciendo el número de objetos que se extienden a lo largo de una ruta desde un objeto. Este método es crucial para estimar el número de objeto devuelto como resultado de una consulta.
• Predicción de la existencia de enlaces: en la predicción del tipo de enlace, se predice el tipo de enlace. Pero aquí el sistema predice si existe un vínculo entre dos objetos. Por ejemplo, esta tarea se utiliza para predecir si existe un enlace entre dos páginas web.
• Reconciliación de objetos: en este método, la función es predecir si dos objetos son iguales en función de sus atributos, rasgos o vínculos. Este método también se denomina incertidumbre de identidad o vinculación de registros. Esta tarea tiene su mismo procedimiento en el cotejo de citas, extracción de detalles, eliminación de duplicados, consolidación de objetos. Por ejemplo, esta tarea es ayudar si un sitio web refleja el otro sitio web como un espejo entre sí.

Desafíos en la minería de enlaces

• Dependencias estadísticas en comparación con las lógicas: la relación lógica entre objetos se indica mediante estructuras de enlace gráfico. La relación estadística se denota por dependencias probabilísticas. El manejo racional de estas dos dependencias es difícil en la minería de datos que es multirelacional. Uno debe ser lo suficientemente cuidadoso para encontrar las dependencias lógicas entre los objetos junto con las relaciones probabilísticas entre los atributos. Estas dependencias ocupan una gran cantidad de espacio, lo que complica el modelo matemático implementado.
• Clasificación y consolidación colectiva: Consideremos un modelo de entrenamiento basado en objetos que tienen etiquetas de clase. En la clasificación convencional, la clasificación solo se realiza en función del atributo. Si existe la posibilidad de que se produzca la clasificación después de dar entrenamiento con objetos sin etiquetar, el modelo se vuelve incapaz de clasificar debido a las complicaciones de las correlaciones de los objetos. Esto exige la necesidad de otro paso iterativo complementario que consolide las etiquetas de los objetos en función de las etiquetas de los objetos vinculados a él. Aquí tiene lugar la clasificación colectiva.
• Uso constructivo de datos etiquetados y no etiquetados: una técnica emergente es fusionar datos etiquetados y no etiquetados. Los datos sin etiquetar ayudan a identificar la distribución de los atributos. Los enlaces que están presentes en los datos sin etiquetar nos ayudan a extraer los atributos del objeto enlazado. Los enlaces que están presentes entre los datos etiquetados y no etiquetados ayudan a establecer dependencias que aumentan la eficiencia en la interferencia.
• Supuestos de mundo abierto en comparación con los de mundo cerrado: en el método convencional, se supone que conocemos todos los objetos/entidades posibles presentes en el dominio que son los supuestos de mundo cerrado. Pero, la suposición de mundo cerrado no es práctica en la aplicación de la realidad. Esto exige la introducción de un lenguaje específico para las distribuciones de probabilidad con respecto a los objetos relacionales que contienen un conjunto variado de objetos.

Minería Comunitaria

El análisis de redes incluye el hallazgo de objetos que se encuentran en grupos que comparten atributos similares. Este proceso se conoce como minería comunitaria. En el enlace de página web, la introducción de comunidad donde se hace un conjunto de páginas web que siguen una temática común. Muchos algoritmos de minería comunitaria deciden que solo hay una red e intentan establecer una relación homogénea. Pero en las páginas web del mundo real, existen múltiples redes con relaciones heterogéneas. Esto demuestra la necesidad de una minería comunitaria multirelacional.