Reduzca la dimensionalidad de los datos usando PCA – Python

Introducción

Los avances en ciencia de datos y aprendizaje automático nos han permitido resolver varios problemas complejos de regresión y clasificación. Sin embargo, el rendimiento de todos estos modelos de ML depende de los datos que se les proporcionen. Por lo tanto, es imperativo que proporcionemos a nuestros modelos de ML un conjunto de datos óptimo. Ahora, uno podría pensar que cuantos más datos proporcionemos a nuestro modelo, mejor se vuelve, sin embargo, no es el caso. Si alimentamos nuestro modelo con un conjunto de datos excesivamente grande (con una gran cantidad de características/columnas), surge el problema del sobreajuste , en el que el modelo comienza a verse influenciado por valores atípicos y ruido. Esto se llama la maldición de la dimensionalidad .

El siguiente gráfico representa el cambio en el rendimiento del modelo con el aumento en el número de dimensiones del conjunto de datos. Se puede observar que el rendimiento del modelo es mejor solo en una dimensión de opción, más allá de la cual comienza a disminuir.

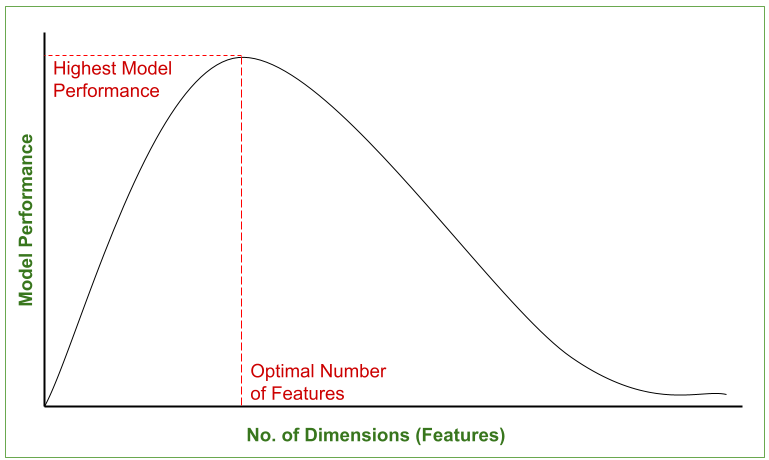
 Rendimiento del modelo frente al número de dimensiones (características) – Maldición de la dimensionalidad

La reducción de dimensionalidad es una técnica estadística/basada en ML en la que tratamos de reducir la cantidad de características en nuestro conjunto de datos y obtener un conjunto de datos con una cantidad óptima de dimensiones.

Una de las formas más comunes de lograr la reducción de la dimensionalidad es la extracción de características, en la que reducimos el número de dimensiones asignando un espacio de características de mayor dimensión a un espacio de características de menor dimensión. La técnica más popular de extracción de características es el análisis de componentes principales (PCA)

Análisis de componentes principales (PCA)

Como se indicó anteriormente, el análisis de componentes principales es una técnica de extracción de características que mapea un espacio de características de dimensiones superiores a un espacio de características de dimensiones inferiores. Mientras reduce el número de dimensiones, PCA asegura que la información máxima del conjunto de datos original se retenga en el conjunto de datos con el número reducido. de dimensiones y la correlación entre los Componentes Principales recién obtenidos es mínima. Las nuevas características obtenidas después de aplicar PCA se denominan Componentes Principales y se denotan como PCi (i=1,2,3…n) . Aquí, (Componente principal-1) PC1 captura la máxima información del conjunto de datos original, seguido de PC2, luego PC3 y así sucesivamente.

El siguiente gráfico de barras muestra la cantidad de variación explicada capturada por varios componentes principales. (La Variación Explicada define la cantidad de información capturada por los Componentes Principales).

Varianza Explicada Vs Componentes Principales

Para comprender los aspectos matemáticos involucrados en el análisis de componentes principales, consulte Enfoque matemático para PCA . En este artículo, nos centraremos en cómo usar PCA en Python para la reducción de la dimensionalidad. 

Pasos para aplicar PCA en Python para la reducción de la dimensionalidad

Comprenderemos el enfoque paso a paso de aplicar el análisis de componentes principales en Python con un ejemplo. En este ejemplo, usaremos el conjunto de datos iris, que ya está presente en la biblioteca sklearn de Python. 

Paso 1: importa las bibliotecas necesarias

Todas las bibliotecas necesarias requeridas para cargar el conjunto de datos, preprocesarlo y luego aplicarle PCA se mencionan a continuación:

# Import necessary libraries
from sklearn import datasets  # to retrieve the iris Dataset
import pandas as pd  # to load the dataframe
from sklearn.preprocessing import StandardScaler  # to standardize the features
from sklearn.decomposition import PCA  # to apply PCA
import seaborn as sns  # to plot the heat maps

Paso 2: Cargue el conjunto de datos

Después de importar todas las bibliotecas necesarias, necesitamos cargar el conjunto de datos. Ahora, el conjunto de datos del iris ya está presente en sklearn. Primero, lo cargaremos y luego lo convertiremos en un marco de datos de pandas para facilitar su uso.

#Load the Dataset
iris = datasets.load_iris()
#convert the dataset into a pandas data frame
df = pd.DataFrame(iris['data'], columns = iris['feature_names'])
#display the head (first 5 rows) of the dataset
df.head()

Producción:

conjunto de datos del iris

Paso 3: Estandarizar las características

Antes de aplicar PCA o cualquier otra técnica de Machine Learning, siempre se considera una buena práctica estandarizar los datos. Para esto, Standard Scalar es el escalar más utilizado. Standard Scalar ya está presente en sklearn. Por lo tanto, ahora estandarizaremos el conjunto de características utilizando Standard Scalar y almacenaremos el conjunto de características escaladas como un marco de datos de pandas.

#Standardize the features
#Create an object of StandardScaler which is present in sklearn.preprocessing
scalar = StandardScaler()
scaled_data = pd.DataFrame(scalar.fit_transform(df)) #scaling the data
scaled_data

Producción:

Conjunto de datos de iris escalado

Paso 3: verifique la correlación entre funciones sin PCA (opcional)

Ahora, verificaremos la correlación entre nuestro conjunto de datos escalados usando un mapa de calor. Para esto, ya hemos importado la biblioteca seaborn en el Paso-1. La función corr() proporciona la correlación entre varias características y luego la función heatmap() traza el mapa de calor. La escala de colores al costado del mapa de calor ayuda a determinar la magnitud de la correlación. En nuestro ejemplo, podemos ver claramente que un tono más oscuro representa una menor correlación, mientras que un tono más claro representa una mayor correlación. La diagonal del mapa de calor representa la correlación de una característica consigo misma, que siempre es 1.0, por lo tanto, la diagonal del mapa de calor tiene el tono más alto.

#Check the Co-relation between features without PCA
sns.heatmap(scaled_data.corr())

Producción: 

Mapa de calor de correlación del conjunto de datos de Iris sin PCA 

Podemos observar en el mapa de calor anterior que la longitud del sépalo y la longitud del pétalo y la longitud del pétalo y el ancho del pétalo tienen una alta correlación. Por lo tanto, evidentemente necesitamos aplicar la reducción de dimensionalidad. Si ya sabe que su conjunto de datos necesita una reducción de la dimensionalidad, puede omitir este paso. 

Paso 4: Aplicación del análisis de componentes principales

Aplicaremos PCA en el conjunto de datos escalado. Para esto, Python ofrece otra clase integrada llamada PCA que está presente en sklearn.decomposition , que ya importamos en el paso 1. Necesitamos crear un objeto de PCA y, al hacerlo, también debemos inicializar n_components, que es la cantidad de componentes principales que queremos en nuestro conjunto de datos final. Aquí, hemos tomado n_components = 3, lo que significa que nuestro conjunto de funciones final tendrá 3 columnas. Ajustamos nuestros datos escalados al objeto PCA que nos da nuestro conjunto de datos reducido.

#Applying PCA
#Taking no. of Principal Components as 3
pca = PCA(n_components = 3)
pca.fit(scaled_data)
data_pca = pca.transform(scaled_data)
data_pca = pd.DataFrame(data_pca,columns=['PC1','PC2','PC3'])
data_pca.head()

Producción:

Conjunto de datos PCA

Paso 5: Comprobación de la correlación entre características después de PCA

Ahora que hemos aplicado PCA y obtenido el conjunto de funciones reducido, verificaremos la correlación entre varios componentes principales, nuevamente mediante un mapa de calor.

#Checking Co-relation between features after PCA
sns.heatmap(data_pca.corr())

Producción:

Mapa de calor después de PCA

El mapa de calor anterior muestra claramente que no hay correlación entre varios componentes principales obtenidos (PC1, PC2 y PC3). Por lo tanto, nos hemos movido de un espacio de características de mayor dimensión a un espacio de características de menor dimensión mientras nos aseguramos de que no haya una correlación mínima entre las PC así obtenidas. Por lo tanto, hemos logrado los objetivos de PCA.

Ventajas del Análisis de Componentes Principales (PCA):

1. Para un funcionamiento eficiente de los modelos ML, nuestro conjunto de funciones debe tener funciones sin correlación. Después de implementar el PCA en nuestro conjunto de datos, todos los componentes principales son independientes, no hay correlación entre ellos.
2. Una gran cantidad de conjuntos de características conducen al problema del sobreajuste en los modelos. PCA reduce las dimensiones del conjunto de funciones, lo que reduce las posibilidades de sobreajuste.
3. PCA nos ayuda a reducir las dimensiones de nuestro conjunto de características; por lo tanto, el conjunto de datos recién formado que comprende los componentes principales necesita menos espacio en disco/nube para el almacenamiento y conserva la máxima información.