La palabra cónica significa algo relacionado con el cono. El cono es una figura 3D, ahora imagina un plano, cualquier plano que pase por el cono, la curva de intersección entre los dos da lugar a diferentes secciones cónicas. En general, hay 3 tipos básicos de secciones cónicas, elipse, parábola e hipérbola. ¿Por qué no se menciona el círculo? Eso es porque el círculo es un tipo especial de elipse con coeficientes x e y iguales. La ecuación que describe todas las secciones cónicas es, ax 2 + 2hxy + by 2 + 2gx + 2fy + c = 0, donde a, b no pueden ser 0 simultáneamente.
La ecuación anterior es la ecuación general de las secciones cónicas. Según los valores de a, b y h, la ecuación indica qué tipo de sección cónica representa.
Circulo
Un círculo se define como el lugar geométrico de todos y cada uno de los puntos que están a la misma distancia de un punto fijo en el plano. En la ecuación general que se usa para representar cualquier tipo de cono, también se puede formar la ecuación del círculo. Si a = b y h = 0,
Entonces se obtiene un círculo y la ecuación se convertirá en ax 2 + ay 2 + 2gx + 2fy +c = 0. Esta es la ecuación general de un círculo. También se puede reescribir de la siguiente manera,
x 2 + y 2 + 2gx/a + 2fy/a + c/a = 0
O, (x + g/a) 2 + (y + f/a) 2 = (g/a) 2 + (f/a) 2 – c/a ⇢ (1)
Este círculo tiene su centro en (-g/a, -f/a) y el radio del círculo es ![]()
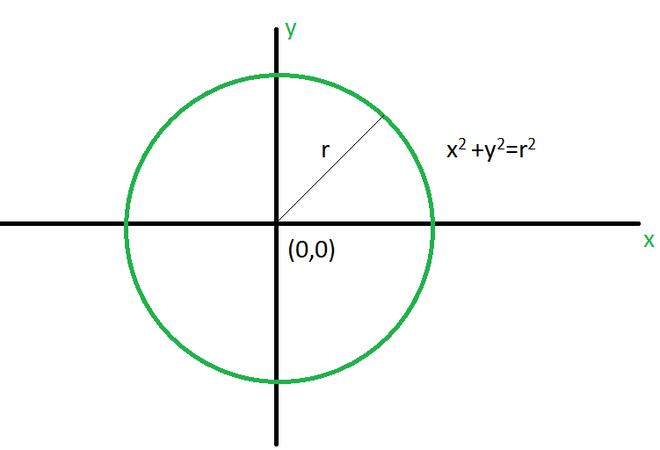
Si la circunferencia tiene su centro en (0, 0) origen. La ecuación del círculo será entonces x 2 + y 2 = 1
Escribe la ecuación del círculo en forma estándar x 2 + y 2 + 6x – 4y – 12 = 0
Solución:
En la pregunta, se pide escribir la ecuación del círculo en forma estándar. La ecuación dada es x 2 + y 2 + 6x – 4y – 12 = 0. De la ecuación en sí, se puede decir que esta es una ecuación de un círculo ya que los coeficientes de xey son iguales. Esta ecuación se puede reescribir de la siguiente manera:
(x + 3) 2 – 9 + (y – 2) 2 – 4 – 12 = 0
O, (x + 3) 2 + (y – 2) 2 = 25
O, (x + 3) 2 + (y – 2) 2 = 5 2
Problemas de muestra
Pregunta 1: Escribe la ecuación de un círculo en forma estándar x 2 + y 2 – 6x – 8y – 1 = 0
Solución:
Compare esta ecuación con la ecuación general del círculo que es ax 2 + ay 2 + 2gx + 2fy + c = 0
Después de comparar, a = 1, g = -3, f = – 4 y c = -1
Ahora que se obtuvieron los valores, uno puede formar fácilmente la ecuación estándar del círculo reemplazando los valores en la ecuación (1),
(x – 3/1) 2 + (y – 4/1) 2 = (-3/1) 2 + (-4/1) 2 + (-1/1)
O, (x – 3) 2 + (y – 4) 2 = 9 + 16 -1
O, (x – 3) 2 + (y – 4) 2 = 24
Pregunta 2: Escribe la ecuación del círculo que tiene su centro en el origen y tiene un radio de 5 unidades.
Solución:
Centro en el origen significa que la coordenada es (0, 0). La ecuación estándar de un círculo es (x – a) 2 + (y – b) 2 = r 2.
Donde (a, b) es el centro del círculo y r su radio.
Aquí, en el centro de la pregunta está (0, 0) y el radio es de 5 unidades. por lo tanto la ecuación de la circunferencia será,
(x – 0) 2 +(y – 0) 2 = 5 2
x2 + y2 = 25
Pregunta 3: Escribe la ecuación de un círculo que tiene su centro en (5,-3) y un radio de 4 unidades.
Solución:
Centro en (5, -3). La ecuación estándar de un círculo es (x – a) 2 + (y – b) 2 = r 2 .
Por tanto la ecuación de la circunferencia será (x – 5) 2 + (y – (-3)) 2 = 4 2
O, (x – 5) 2 + (y + 3) 2 = 16
Pregunta 4: Encuentra el centro y el radio del círculo que está definido por la ecuación x 2 + y 2 – 2x + 8y – 8 = 0.
Solución:
La ecuación anterior se puede reescribir como x 2 – 2x + 1 + y 2 + 8y + 16 = 8 + 1 +16
O, (x – 2) 2 + (y + 4) 2 = 25
O, (x – 2) 2 + (y + 4) 2 = 5 2
Publicación traducida automáticamente
Artículo escrito por rajarshiban13 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA